考察
 A,Bを互いに素とする。Bは奇数としておく。
0≦m<AB な整数mに対して
yB≡m (mod A)となるyを0≦y<A の範囲でとれる。
そうすると整数x,yで m=yB-xA と表されることになる。
このmから(x,y)への対応を、x=X(m),y=Y(m)と名付けておく。
点(x,y)が所属する範囲は
0≦y<A, 0≦yB-xA<ABで表される平行四辺形である
このうちx>0 に存在する格子点が、
Ax+By (x,y∈{0}∪N) で表せない整数に相当している。
その個数は (A-1)(B-1)/2 であるがこの定数をC/2と名付けておく。
そのうち、{(x,y)|0<x≦X(m)かつY(m)≦y<A}に存在する格子点が
Ax+By+m で新しく表すことができる整数となる。
そこで、m,2m,..,nm,に対して同様に長方形をくり抜くようなイメージで
Ax+By+nm で表すことができる整数の個数を評価することができる。
x<B/2のとき
f(m) = g(x,y) = C/2 - Σx(A-ny) [ n∈N, ny<A ]
x≧B/2 のとき
f(m) = g(x,y) = C/2 - Σ(A-y)(B+n(x-B)) [n∈N, B+n(x-B)>0]
m=yB-xA, x=X(m), y=Y(m)の関係である。
----------
x<B/2のとき
f(m) = g(x,y) = C/2 - Σx(A-ny) [ n∈N, ny<A ]
x≧B/2 のとき
f(m) = g(x,y) = C/2 - Σ(A-y)(B+n(x-B)) [n∈N, B+n(x-B)>0]
シグマを展開してそれぞれn=A/y,n=B/(B-x) を代入すると
[非整数的補間するという操作である]
x<B/2のとき
f(m)≒ C/2 - x(A-y)A / 2y
x≧B/2 のとき
f(m)≒ C/2 - x(A-y)B / 2(B-x)
・yを固定してxを1ずつ変化させるとmは公差Aで変化し、
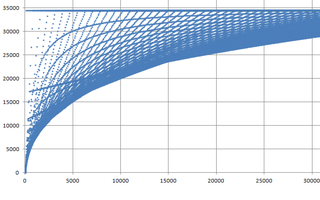
散布図に見られる直線および分数関数曲線に対応する。
--------
・次に知りたいのはmを狭い範囲に絞った時のg(x,y)の下限である。
m=yB-xAを固定した時の g(x,y)の下限として考察すれば良い。
yの関数として考察する。対称的な挙動からx<B/2の場合を扱えば良い。
y=sqrt(mA/B)のときが下限に相当し、
f(m) = C/2 + sqrt(ABm) - (AB+m)/2 という式を得る。
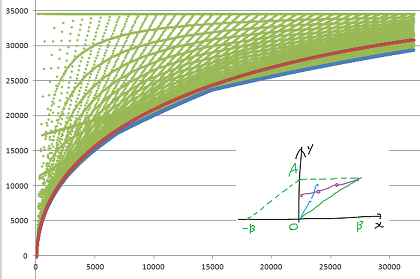
確かに傾向をよく再現しているが、
非整数的補間の影響と思われるずれが見られる(図の赤線)
そこで補間せず整数的に調べてみると次の結果を得た:
L[n] = AB(1-sqrt(n/(n+2)))/(n+1) とおく。
L[n]はL[0]=ABから0に向かう単調数列である。
L[n]≦m≦L[n-1] のとき
f(m) = C/2 - ABn((n+1)(m/AB)-2)^2/(8n+8)
これは、放物線の断片をつなぎ合わせたものである。(図の青線)
nが大きくなると断片は小さくなり、包絡線で近似できる(図には加えてない)
f(m)=(C-AB)/2 + ((m+16AB)sqrt(m^2+16ABX)+m^2-40ABm)/64
最初に示したA=89,B=878のf(m)のグラフにおいて
下限が折れ曲がっている所に相当するのは
確かにL[1]≒14801,L[2]≒6838 である
A,Bを互いに素とする。Bは奇数としておく。
0≦m<AB な整数mに対して
yB≡m (mod A)となるyを0≦y<A の範囲でとれる。
そうすると整数x,yで m=yB-xA と表されることになる。
このmから(x,y)への対応を、x=X(m),y=Y(m)と名付けておく。
点(x,y)が所属する範囲は
0≦y<A, 0≦yB-xA<ABで表される平行四辺形である
このうちx>0 に存在する格子点が、
Ax+By (x,y∈{0}∪N) で表せない整数に相当している。
その個数は (A-1)(B-1)/2 であるがこの定数をC/2と名付けておく。
そのうち、{(x,y)|0<x≦X(m)かつY(m)≦y<A}に存在する格子点が
Ax+By+m で新しく表すことができる整数となる。
そこで、m,2m,..,nm,に対して同様に長方形をくり抜くようなイメージで
Ax+By+nm で表すことができる整数の個数を評価することができる。
x<B/2のとき
f(m) = g(x,y) = C/2 - Σx(A-ny) [ n∈N, ny<A ]
x≧B/2 のとき
f(m) = g(x,y) = C/2 - Σ(A-y)(B+n(x-B)) [n∈N, B+n(x-B)>0]
m=yB-xA, x=X(m), y=Y(m)の関係である。
----------
x<B/2のとき
f(m) = g(x,y) = C/2 - Σx(A-ny) [ n∈N, ny<A ]
x≧B/2 のとき
f(m) = g(x,y) = C/2 - Σ(A-y)(B+n(x-B)) [n∈N, B+n(x-B)>0]
シグマを展開してそれぞれn=A/y,n=B/(B-x) を代入すると
[非整数的補間するという操作である]
x<B/2のとき
f(m)≒ C/2 - x(A-y)A / 2y
x≧B/2 のとき
f(m)≒ C/2 - x(A-y)B / 2(B-x)
・yを固定してxを1ずつ変化させるとmは公差Aで変化し、
散布図に見られる直線および分数関数曲線に対応する。
--------
・次に知りたいのはmを狭い範囲に絞った時のg(x,y)の下限である。
m=yB-xAを固定した時の g(x,y)の下限として考察すれば良い。
yの関数として考察する。対称的な挙動からx<B/2の場合を扱えば良い。
y=sqrt(mA/B)のときが下限に相当し、
f(m) = C/2 + sqrt(ABm) - (AB+m)/2 という式を得る。
確かに傾向をよく再現しているが、
非整数的補間の影響と思われるずれが見られる(図の赤線)
そこで補間せず整数的に調べてみると次の結果を得た:
L[n] = AB(1-sqrt(n/(n+2)))/(n+1) とおく。
L[n]はL[0]=ABから0に向かう単調数列である。
L[n]≦m≦L[n-1] のとき
f(m) = C/2 - ABn((n+1)(m/AB)-2)^2/(8n+8)
これは、放物線の断片をつなぎ合わせたものである。(図の青線)
nが大きくなると断片は小さくなり、包絡線で近似できる(図には加えてない)
f(m)=(C-AB)/2 + ((m+16AB)sqrt(m^2+16ABX)+m^2-40ABm)/64
最初に示したA=89,B=878のf(m)のグラフにおいて
下限が折れ曲がっている所に相当するのは
確かにL[1]≒14801,L[2]≒6838 である