[1] 原点でブローアップされた射影平面X、因子、ピカール群の観察 [2] 原点を通らない因子Cと例外因子E、オイラー標数の計算 [3] 交点数 [4] ヒルツェブルフ曲面
[1] 原点でブローアップされた射影平面Xを考える： Xは、P^2×P^1 = Proj[x,y,z]×Proj[u,v] を部分集合xv-yuで割ったものとして描写できる。 P^2の点[x:y:z]=[0:0:1]を「原点」と呼んでいる。 Xは集合としては、「原点を通る直線L∈P^1と、その上にある点p∈P^2の組」と解釈することができる。 （pが原点でないときは、Lは[u:v]=[x:y]によって1つに定まり、pが原点のときは、Lは全方向許される） これを略式に、原点に全方向を表す点を詰め込んだようなものとイメージできる（が正確には代数的に考察することになる）。 この原点の上にある部分が、例外因子と呼ばれる。 [1-a] Xのアフィン被覆 Xは、4つのアフィン平面で被覆される。 斉次座標による描写と、非斉次座標は以下のようになる。 U1: u,z≠0, (x[02],u[10]) x[12]=x[02]*u[10] (y=0はx=0のみ許される) U2: v,z≠0, (x[12],u[01]) x[02]=x[12]*u[01] (x=0はy=0のみ許される) U3: x,u≠0, (x[10],x[20]) u[10]=x[10] U4: y,v≠0, (x[01],x[21]) u[01]=x[01] で被覆される。 非斉次座標の変換は、形式的に x[02]=x/z, x[12]=y/z, u[01]=u/vなどと解釈することで得られる。 例えばU1→U2では: x[12]=u[10]*x[02], u[01]=1/u[10] という変換である。 最初はこの非斉次座標で考察を進めていたが、混乱しやすかった。 x[02]=x, x[12]=y とおいた「略式座標」で考察を進めると様子が分かりやすかったのでここではこうする。 （あとで零点と極を考えるときには、x,yの代わりにx/z, y/zを使った方が考えやすかったのでそこではそうする。） 略式に、1/x,1/y,x/y,y/xという変数があると考える。 x=y=0において、x/y,y/xがいろいろな値を取り得て、これが例外因子をなすという状況である。 ・[x:y:1]を平面的に描写したイメージではXは次のように被覆される。 U1はy=kxの形の直線が掃く範囲(赤) U2はx=kyの形の直線が掃く範囲(青) U3はx≠0を除き、無限遠点を合わせたもの(紫) U4はy≠0を除き、無限遠点を合わせたもの(緑) 原点においては、U1とU2が、例外直線の稠密な開集合を含んでいる。
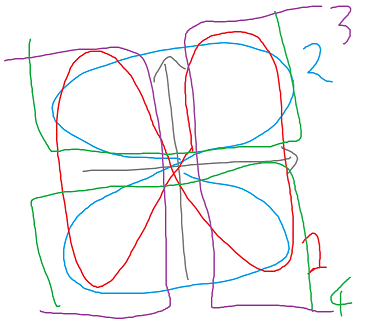・それぞれのアフィン平面をxy平面的に描写したものも考えた。
ここでは、z=1とおいた略式な座標を使っている。
色で矢印をつけたC,L1,L2,Eがそれぞれ貼り合わさる。Eが例外因子に対応する。
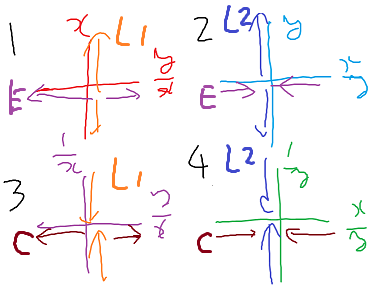U1とU2は、U1のx軸(L1)を除いた部分と、U2のy軸(L2)を除いた部分が反対向きに貼り合わさる。
U1とU3は、U1の(y/x)軸(E)を除いた部分と、U3の(x/y)軸(C)を除いた部分が反対向きに貼り合わさる。
U1とU4や、U2とU3の場合は、すべての座標軸(C,E,L1,L2)を除いた部分で貼り合わさる。
こう見ると貼り合わせは対称的な感じがするが（後で利用する）、
貼り合わせの様子まで見ると対称的ではない。
U1の横線x=kは、U2に移ると双曲線 (x/y)(y)=k に移るが、
U3の横線1/x=kは、U4に移ると原点を通る直線 (1/y)/(x/y)=k に移る。
・略式座標でxという関数の零点と極をアフィンごとに観察できる：
U1では x: Eで零点を持つ。
U2では (x/y)y = 0: EとL2で零点を持つ
U3では 1/x : Cで極を持つ
U4では (1/y)/(x/y): L2で零点を持ち、Cで極を持つ
---
[1-b] 因子とピカール群の観察
ヴェイユ因子は前回のノートの[2-c]で触れた。
「余次元1で正則」という条件を前提とする。（今回の例では満たされている）
ヴェイユ因子とは、余次元1の既約閉集合の形式的な整数係数線形結合である。
有理関数fがあるとき、fの零点と極によってdiv(f)という因子が定義できる。
注意：曲線上の関数では、零点や曲は文字通り点であったが、曲面上の関数の零点や曲は、曲線である。
例えばxy平面上のxy/(x+y)と言う関数はx軸とy軸で零点を持ち、直線x+y=0で極を持つ、と言う。
このように書ける因子を主因子と言う。
開アフィンごとに主因子で書けるようなものを局所主因子と言う。
＊局所主因子ではないヴェイユ因子の例は14.2.Hで紹介されている円錐の母線がある。
＊ネーターで分解的なスキームでは、ヴェイユ因子は局所主因子であり、
今回の考察対象ではそうであるから、難しく考えなくてよい。
＊ピカール群は、局所主因子を主因子で割った群(14.2.7)である。
従って今回の考察対象では、ヴェイユ因子を主因子で割った群と考えても良い。
＊2つの因子の差が主因子であるときにそれらを「線形同値」と呼ぶ。
この言葉を使うと、主因子で割った群とは、線形同値類である。
・アフィン曲面では、すべての因子が主因子だから、ピカール群は自明である。
・射影平面では、零点と極の合計が等しいものはすべて主因子である。
従って2つの因子は、(零点の個数)-(極の個数)が等しければ線形同値で、ピカール群は整数群である。
（例えば射影平面で斉次座標で描写すると、(x-z)で零点を持ち、zで極を持つ有理関数は(x-z)/zである。）
・今回のXの場合を観察する。
先に名付けたC,E,L1,L2が、余次元1の既約閉集合の例となり、それぞれ自体はP^1に同型である。
いくつかの有理関数による主因子を観察すると、
div(x/y) = [L2]-[L1]
div(x/z) = [L2]+[E]-[C] ([1-a]の最後で観察した)
div(y/z) = [L1]+[E]-[C]
となるので、[L1]と[L2]が線形同値、[E]と[C]-[L1]が線形同値であることが分かる。
・より一般に原点を通る直線同士も互いに線形同値である。
・Xは原点以外では射影平面と同じように振る舞うから、原点を通らない直線は互いに線形同値である。
・後でわかることには [C]と[E]は独立である：a[C]とb[E]が線形同値ならばa=b=0である。
従ってXのヴェイユ因子の線形同値類は、a[C]+b[E]の形で一意的に表される。すなわちXのピカール群はZ＋Zである。
＊フィブリレーション(20.2.8)の視点：全射X→P^1があって各点の逆像がP^1に同型なとき、
P^1上の2点p,qに対して、pを零点に持ち、qを極に持つP^1上の有理関数がある。
これをXに引き戻すことで、pの逆像とqの逆像は線形同値である。
[2] オイラー標数の計算 上記で名付けた因子に付随する可逆層O(C)やO(E)のオイラー標数をチェックコホモロジーに従って計算する。 これらは前回のノートの[3]で定義した。 チェック複体を考える: 0→ΠO(Ui) → ΠO(Uij) → ΠO(Uijk) → O(U1234)→ 0 0→(f1,f2,f3,f4) → (f12,f13,f14,f23,f24,f34) → (f123,f124,f134,f234) → f(1234)→ 0 写像は具体的に： (f1,f2,f3,f4)→(f1-f2, f1-f3, f1-f4, f2-f3, f2-f4, f3-f4) (f12,f13,f14,f23,f24,f34)→(f12-f13+f23, f12-f14+f24, f13-f14+f34, f23-f24+f34) (f123,f124,f134,f234)→(f123-f124+f134-f234) U123, U124, U134, U234, U1234 は U14,U23と同じで、 どのアフィンを基準にしても両方の座標軸が除かれたものだから（[1]で観察した） x,y,zの任意の負冪を含めた任意の単項式がこの開集合全体で正則となる。 （斉次座標を使っているから、分子と分母が同じ次数になる必要がある。） --- [2-a] (f1-f2, f1-f3, f1-f4, f2-f3, f2-f4, f3-f4)がすべて0ならば、f1,f2,f3,f4は0か： これは大域切断があるかどうかに相当する：これがH^0に対応する。 大域切断があるとすれば少なくとも、U14上で正則だから、x,y,zの単項式fを考えれば良い。 fは x/yの適当な冪とx/zの適当な冪を掛け合わせたものとして表せるから、 div(f)は div(x/y)=[L2]-[L1] と div(y/z)=[L1]+[E]-[C] の線形結合である。 構造層の大域切断は、一般論の通り、定数関数のみである。 ・Cでm位の極を許した有理関数の層O(m[C])では、x/z, y/zを合計m個まで掛け合わせたものが大域切断となる。 ・L1でm位の極を許した有理関数の層O(m[L1])では、x/yをm個まで掛け合わせたものが大域切断となる。 ・Eのみで極を許した有理関数の層では、定数関数以外に大域切断はない。 （Cで正則にしようとするとL1とL2のどちらかが極になってしまうから） そういうわけで、m≧0のとき h^0(O(m[C])) = (m+1)(m+2)/2 h^0(O(m[E])) = m+1 h^0(O(m[E])) = 1 1つの因子で零点を持ち、他で正則な大域切断は存在しないから、 m＜0ではこれらのh^0すべて0である。 --- [2-b] (f12-f13+f23, f12-f14+f24, f13-f14+f34, f23-f24+f34)がすべて0ならば、 それらに移る(f1,f2,f3,f4)があるか：これ（の無さ具合）がH^1に対応する どこで正則か＝極の種類で場合分けすれば良い。 C,E,L1,L2以外に極を持つものは、どのUijでも定義されないから、やはりx,y,zの単項式ごとに考えれば良い。 [a] C,E,L1,L2全部で極な場合 f14,f23のみが非零になるが、例えばf12-f14+f24=0よりf14=0で、同様にf23=0だから、全部0な組しかない。 [b] E,L1,L2で極な場合（例えばzz/xy） f14,f23,f34が非零になり得る。しかしf12-f13+f23=0よりf23=0なので、これも全部0だと要求されてしまう。 [c1] E,L1が極な場合（例えばz/y） f13,f14,f23,f34が非零になり得て、f3を非零にして良い。 f12-f14+f24=0からf14=0が要求され、残りはf23=f13=-f34が要求されるのでこれを-f3とすれば良い。 [c2] L1,L2が極な場合 f12,f14,f23,f34が非零になり得て、f1,f2,f3,f4は全部0である。 f12=-f23=f34=f14=A, f13=f24=0 の形をした組に対して、これに移る(f1,f2,f3,f4)がない。 [d] Cのみ極な場合(例えばy/z) f12,f13,f14,f23,f24が非零になり得て、f1,f2を非零にして良い。 f34=0, f13=f14=A, f23=f24=B, f12=A-B の形をした組に対して、f1=A,f2=Bとすれば良い。 [e] 極が無い場合 f34=C, f13=A,f14=A+C, f23=B,f24=B+C, f12=A-B の形をした組に対して、f1=A,f2=B,f4=-Cとすれば良い。 [1-a]で見た貼り合わせの対称性により、これらで本質的にすべてである。 [c2]のパターンの時に非自明なコホモロジーが発生する。このパターンには、C,Eが極な場合も該当する。 再掲：div(f)は div(x/y)=[L2]-[L1] と div(y/z)=[L1]+[E]-[C] の線形結合である。 これらの線形結合では[c2]のパターンは作れないことが観察され、確かに構造層のH^1は自明である。 Eで極を持つことが許されたO(mE)では、例えばdiv(zz/xy)=2[C]-2[E]-[L1]-[L2] がパターン[c2]に該当する。 Eで零点を持つことが要求されたO(-mE)では：div(x/z),div(y/z)が自明でないコホモロジーを生成する。 そういうわけで、 H^1(O(2[E]))は zz/xy で生成される1次元ベクトル空間、 H^1(O(3[E]))は zz/xy,zzz/xxy,zzz/xyy で生成される3次元ベクトル空間、 H^1(O(m[E]))は分母にx,yが共に現れ、合計してm次以下となるような単項式で生成され、 m＞0(結果的にm≧0でも良い)のとき、h^1(O(m[E])) = (mm-m)/2 mが負の場合は H^1(O(-2[E]))は x/z,y/zで生成される2次元ベクトル空間、 H^1(O(-3[E]))は x/z,y/z,xx/zz,xy/zz,yy/zzで生成される5次元ベクトル空間、 このようにして、m＜0のときh^1(O(m[E])) = (mm-m-2)/2 同様に考察すると： O(m[C])の場合はコホモロジーが生まれないことが分かる。なぜなら： ・L1,L2を極にしようとするとEも極になってしまう ・Eを極にしようとすると、L1かL2も極になってしまう O(m[L1])の場合、E,Cを同時に極にすることができないが、L1,L2を極にすることができる： L1で2位以上の零点を要求するとき(m≧2)の[L1]-[L2]が自明でないコホモロジーを生成する。 H^1(X,O(-2[L1]))は、y/xで生成される。 H^1(X,O(-3[L1]))は、y/x,yy/xxで生成される。 こうして、m≦-2のとき、h^1(X,O(m[L1]))=-(m+1) --- [2-c] f123-f124+f134-f234 = 0 ならば、 それに行く組(f12,f13,f14,f23,f24,f34)があるか：これ（の無さ具合）がH^2に対応する。 [a] C,E,L1,L2全部で極な場合 f123-f124+f134-f234=0 を満たす組は3次元だが、 fijについてはf14,f23のみを非零にして良いから2次元しか生成できず、1次元分のコホモロジーが発生する。 [b] E,L1,L2で極な場合（例えばzz/xy） f14,f23,f24を非零にして良い。 f23 = f123, f14 = -f124, f34 = f134+f14, f12=f13=f34=0 とおけば良い。 もっと極が少ない場合も、f14,f23を含む少なくとも3つを非零にして良いので同様である。 従って自明でないH^2を与えるのは[a]しかない。 再掲：div(f)は div(x/y)=[L1]-[L2] と div(x/z)=[L1]+[E]-[C] の線形結合である。 これらの線形結合は[a]にはならないから構造層のH^2は自明である。 O(-3[C])では、div(zz/xy)=2[C]-[L1]-[L2]-2[E] が [a]のパターンになる。 O(-m[C])では、分子にx,yが共に現れ、分母のzの次数がmより小さい単項式のとき、 そのような単項式の種類は(m-1)(m-2)/2であり、 従って、(mの符号を変えて) m＜0のとき h^2(X,O(m[C]))=(m+1)(m+2)/2 O(m[E])の場合、Cを極にしようとするとL1,L2のどちらかが零点になってしまう。 O(m[L1])の場合、E,Cを同時に極にすることができない すなわちh^2(X,O(m[E]))=0h^2(X,O(m[L1]))=0 --- [2-d] 以上をまとめると、以下のような結果になる： ・O(m[C])については、前回のノートの[3]の最後に書いた結果と同じで、 m≧0のとき h^0(X,O(mC))=(m+1)(m+2)/2 m＜0のとき h^2(X,O(mC))=(m+1)(m+2)/2 ・O(m[E])については m≧0のとき、h^0(X,O(mE))=1, h^1(X,O(mE))=(mm-m)/2 m＜0のとき、h^0(X,O(mE))=0, h^1(X,O(mE))=(mm-m-2)/2=(m+1)(m-2)/2 ・O(m[L1])については m≧0のとき、h^0(X,O(m[L1]))=m+1 m＜0のとき、h^1(X,O(m[L1]))=-(m+1) オイラー標数χ(X,F)はh^iの交代和Σ(-1)^i*h^i(X,F)で定義されるのだった。 それぞれのh^iでは、mによって場合分けされていたものが、 交代和をとると、なんと次のように場合分けせずに1つのmの多項式で表される： χ(X,O(m[C]))=(m+1)(m+2)/2 χ(X,O(m[E]))=-(m+1)(m-2)/2 χ(X,O(m[L1]))=m+1 これは一般的に成り立つ事実である(20.1.I「漸近的リーマンロッホ」) （実は最初はなかなか合わず、h^iの計算の間違いを探すのに時間がかかった。）
[3] 交点数(21章) Xの因子D,D'交点数D・D'は、χ(X,O)-χ(X,O(-D))-χ(X,O(-D'))+χ(X,O(-D-D'))と定義される。 （交点数自体はもっと一般的に定義されるが、ここではこの形のみを扱う。） これは、O(D')をDに制限した時の、曲線D上の因子としての次数（前のノートで定義）とも一致する。 射影平面P^2においては、Dがs次の因子、D'がt次の因子のとき、定義に沿った計算は D・D' = 1 - (-s+1)(-s+2)/2 - (-t+1)(-t+2)/2 + (-s-t+1)(-s-t+2)/2 = st となって、 実際に「交点の個数」を与える。 今回のCは射影平面の1次の因子と同じ挙動をする。すなわちC・C=1である。 ところが、E・Eをこれに従って計算すると、E・E=-1を得る。 実は交点数は多重線形性が成り立つ。E・Eの代わりに(-E)を使っても確認できる： E・E = χ(X,O) - 2χ(X,O(-E)) + χ(X,O(-2E)) = 1+0+0-2 = -1 E・(-E) = 2χ(X,O) - χ(X,O(E)) - χ(X,O(-E)) = 2-1-0 = 1 (-E)・(-E) = χ(X,O) - 2χ(X,O(E)) + χ(X,O(2E)) = 1-2+0 = -1 [追記] L1・L1=0 も同様に確認できるが、これはL1とL2は交わらないからL1・L2=0であり、 [L1]と[L2]が線形同値だからL1・L1=0も得られる。 そうすると、[E]=[C]-[L1]であることを利用して、 E・E = ([C]-[L1])・([C]-[L1]) = 1 - 2 + 0 = -1 と計算することもできる。 （[C]・[L1]=1は1点で交わることから。） --- [追記] 曲面における交点数は、deg_D i^* O(D') としても計算できる。 これは、閉埋め込み D→X によって O(D')を引き戻した層の、Dにおける次数である。 （1次元射影曲線上の次数は前のノートのようにして定義できた。） 共通成分を持たない場合は、これは、D∩D'がD上の因子となり、その次数で良い。 共通部分を持つ場合の閉埋め込みによる引き戻しは、少しややこしい。 ・D=D'=C の場合 閉部分スキームCは、U3,U4を制限したアフィンV3,V4で被覆されるので、 引き戻した層i^* O(C)を考察するにはV3,V4での切断を考察すれば良い。 閉埋め込みV3→U3は、略式座標で、k[y/x,1/x]→k[y/x], 1/x=0 で描写される。 層の引き戻しは、逆像k[1/x,y/x]-加群を、環k[y/x]とテンソルして、k[y/x]加群にして得られる。 逆像は、V3を含む開集合上の切断を、V3を含む開集合への制限で同じになるものを同一視したものである。 一旦 k[X,Y]→k[X], Y→0 とおく。 V3を含む開集合上の構造層の切断は、X,Yの有理式で分母がY=0と交わらないものである。 しかし分子のYは、k[X,Y]上でk[X]とテンソルするときに消えるので、結局 k[X]ということになる。 同様に、V3にO(C)を引き戻した結果は、略式に、k[X]/Y ということになる。 同様に、V4を含む開集合上のO(C)の切断は、略式に、k[X']/Y'ということになる。 変数を元に戻すと、V3上では、x*k[y/x], V4上ではy*k[x/y]ということになる。 大域切断は、x,y がある。このようにして、射影直線上のO(1)と同じ状況であることが確認できる。 ・D=D'=E の場合 U3,U4の代わりにU1,U2で同様に考える。X=y/x, Y=x, X'=x/y, Y'=y で同様の考察となる。 V1上では k[y/x]/x, V2上ではk[x/y]/y ということになる。 大域切断もない。V1上で正則な1/xは、V2の原点で、1位の極であることが確認でき、 こうしてこの層の次数が-1であることがこの視点でも観察できる。 --- ＊交点数の興味深い応用(18.4.5) 「X,Y,Zがa00,..,a22の有理式で、 a00*X^2+a01*XY+a11*Y^2+a02*XZ+a12*YZ+a22*Z^2=0 を満たすようなものは、 自明なものX=Y=Z=0しか存在しない。」という事実を次のようにして示される： Proj[x0,x1,x2]×Proj[a00,a01,a11,a02,a12,a22]から、Σaij*xi*xj=0で切り取られるスキームCを考える。 直線Lと点qを適当に取る。 Cのピカール群は、「Lに相当する因子」D_Lと「qを通る2次曲線に相当する因子」D_qで生成される。 Kをr∈P^5上のファイバーとする。D_L・K=2でD_q・K=0となる。 このことから、任意の因子とKとの交点数は偶数である。 ところが目的の自明でない有理式があったとすると、 それに対応するCの因子は、Kと重複度1で交わるので矛盾する。 ＊21章のタイトルは、交点数のglimpseと書いてある。 本格的には例えば以下のような教材が見当たるが、手ごわい・・ ・Vakilさんによる講義（教材付き）https://math.stanford.edu/~vakil/245/ ・The Stacks ProjectのPart3、43章がそれっぽい
[4] ヒルツェブルフ曲面(17.2.4) これは相対的Proj構成を使って定義される。 P^1上の準連接層O＋O(n)の対称代数構成に付随する相対的射影スキームYを考える。 ここでは、まずはn=1の場合を考える。 A^1=Spec k[x]上では、(u,v)∈O＋O(1)で生成される多項式のProj構成、 A^1'=Spec k[X]上では、(U,V)∈O＋O(1)で生成される多項式のProj構成、 対称代数とは、略式に、Oの元とs個と、O(1)の元をt個掛け合わせたものによってs+t次部分が生成される環である。 u,vは個数をカウントするために便宜的に持ち出された変数と解釈できる。 （より簡単な例：Z上の階数2の自由加群Z＋Zの対称代数は、2変数多項式環Z[u,v]である。 1つ目の成分をs個、2つ目の成分をt個掛けたものは、u^s*v^tという単項式の係数として扱っている。） Oの元がk[x]からk[X]に移るときには、x=1/Xの変換をすれば良い。 O(1)の元がk[x]からk[X]に移るときには、x=1/Xの変換をしてからX^n, n=1ならXを掛けることで対応する。 (前回のノートの[2-a]参照) そういうわけで： f(x)*u は f(1/X)*U に送られる。例えば(ax+b)u は (a/X+b)U に送られる。 f(x)*v は X*f(1/X)*V に送られる。例えば(ax+b)v は (a+bX)V に送られる。 Yは次の4つの開アフィンで被覆される： U1 = Spec k(x, u[01]) U2 = Spec k(X, U[01]) U3 = Spec k(x, u[10]) U4 = Spec k(X, U[10]) x=1/X, U[01]=u[01]/x, u[01]=U[01]/X, U[10]=x*u[10], u[10]=X*U[10] の関係である。 ＊これは例えば、U[01]=U/V=u/vx=u[01]/xと由来する ＊O＋O(n)から構成されるものとO＋O(-n)から構成されるものは同型であることが観察される： U[01]とU[01]の役割を入れ替えれば良い。 U1での「横線」u[10]=kをU2に移すと、双曲線X*U[10]=kに移る。 U3での「横線」u[01]=kをU4に移すと、原点を通る直線 U[01]/X=k に移る。 この様子は、[1-a]で紹介した貼り合わせの様子と同一である。 すなわち、実はn=1のヒルツェブルフ曲面は、[1]で描写したブローアップXと同型である。 https://mathoverflow.net/questions/122952/on-a-hirzebruch-surface この考察は、相対的Projを具体的に考える良い経験になった。 ＊n=0のヒルツェブルフ曲面は、P^1×P^1に同型である。以下の2つが同型らしい。(22.4.K) ・P^2を異なる2点p,qでブローアップしたもの＝Xをさらにブローアップしたもの ・P^1×P^1を1点でブローアップしたもの この同型は、大雑把に1番目の曲面上のxに対して(直線xpの傾き, 直線xqの傾き)∈P^1×P^1を対応させることで得られる。 ブローアップについての事実の紹介(22.4.12) ・広中の定理：標数0の多様体の特異点は滑らかな部分多様体でのブローアップによって解消される ・弱分解定理(Weak Factorization Thorem, https://arxiv.org/abs/math/9904076)： 双有理同型な多様体X,Yは滑らかな部分多様体でのブローアップとブローダウンを有限回繰り返して移りあえる
2020/06/26