$[x:y:z:w]=[s^3:s^2t:st^2:t^3] \in \mathbb{P}^3$ とパラメータづけられるねじれ3次曲線というのがある。
これが3次曲線であることは、例えば平面$x=w$との交点が$[1:1],[1:\omega]:[1:\omega^2]$の3点であることから分かる。
一方で、この曲線は、2つの2次曲面 $xz-y^2=0, yw-z^2=0$ で切り取られるように見える。
そうすると4次曲線という計算になる。何が間違っているか？

$xz-y^2=0, yw-z^2=0$ が切り取るものは、その3次曲線と別の直線$y=z=0$の和集合となっているから。
3つの方程式$xz-y^2=0, yw-z^2=0, xw-yz=0$を使えば、ねじれ3次曲線だけを切り取れる。
しかしこれらは横断的に交わらないので、この次数の情報から曲線の次数は直接得られない。
この現象は、最後の[4]で本題に関してまた現れる。
▲▲

$\mathbb{P}^2$から$\mathbb{P}^2$への3次写像$[x:y:z] \to [x^3:y^3:z^3]: \mathbb{P}^2 \to \mathbb{P}^2$ のグラフ、すなわち、
$([x:y:z],[x^3:y^3:z^3])$ でパラメータづけられる$\mathbb{P}^2 \times \mathbb{P}^2 $の2次元部分多様体$\Gamma$を考える。
先の言葉を使うと、その類は、$[\Gamma] = a\alpha^2+b\alpha\beta+c\beta^2$とおける。（「未定係数法」）
係数$a,b,c$を求めるにはどうすれば良いか？

これを求める常套手段がある。
Chow群の積$[\Gamma] \cdot \alpha\alpha$を考えると、$\alpha$の3次以上は消えるから、$c\alpha^2\beta^2$だけ残る。
同様に、$[\Gamma] \cdot \alpha\beta$を考えると$b$の項だけ残り、$[\Gamma] \cdot \beta\beta$を考えると$a$の項だけ残る。

そこで、$\alpha$や$\beta$に相当する類を具体的に与えて交叉を求めることで$a,b,c$を求められる。
$([x:y:z],[s:t:u]) \in \mathbb{P}^2 \times \mathbb{P}^2$ のうち、
類が$\alpha$であるような超平面$H_1:x=0, H_2:y=0$、
類が$\beta$であるような超平面$H_3:s=t, H_4:s=u$を考えると、
$\Gamma\cap H_1\cap H_2$は $([0:0:1],[0:0:1])$ の1点
$\Gamma\cap H_1\cap H_3$は $([0:0:\omega^k],[0:0:1]) [k=0,1,2]$ の3点
$\Gamma\cap H_3\cap H_4$は $([1:\omega^j:\omega^k],[0:0:1]) [j,k=0,1,2]$ の9点と観察できる。
と数えられる。（正式にはこれらの交わりが「横断的である」ことも確認する必要がある）
こうして、$a=1,b=3,c=9$が得られた。

＃一旦$[\Gamma]=\alpha^2+3\alpha\beta+9\beta^2$が分かれば、他の部分多様体との交点数を計算できるのが、交叉理論の利点である。
例えば、$\Delta=([x:y:z],[x:y:z])$ と $\Gamma$ の交点数は、先と同様にして $[\Delta]=\alpha^2+\alpha\beta+\beta^2$ を得ることで、
$[\Gamma][\Delta] = (\alpha^2+3\alpha\beta+9\beta^2)(\alpha^2+\alpha\beta+\beta^2)$ と計算できる。
$\alpha,\beta$ の3次以上が消えることから、この結果は $13\alpha^2\beta^2$、すなわち13点である。

今回の3次写像の場合ではこの13点は$x:y = x^3:y^3$ を整理した $xy(x+y)(x-y)=0$ 等から実際に求められる：
$[1:1:1],$
$[-1:1:1],[1:-1:1],[1:1:-1],$
$[1:1:0],[1:0:1],[0:1:1],$
$[1:-1:0],[1:0:-1],[0:1:-1],$
$[1:0:0],[0:1:0],[0:0:1],$
の13点が、$[x:y:z]=[x^3:y^3:z^3]$を満たす13点である。
▲▲

超曲面$Y_i$の次数を求めるには、直線との交点を数えれば良い。

ここでは具体的なものを使って説明する。
$\mathbb{P}^5$のある超曲面に対応する、円$x^2+y^2=z^2$に接する2次曲線の集合$Y_i$と、
$\mathbb{P}^5$のある直線に対応する、直交双曲線族$sxy=tz^2$の交わりの個数を考える。
（すなわち、円$x^2+y^2=z^2$に接するこの形の直交双曲線の個数を考える。）

$C_i$をパラメータ表示する。この場合は$[x:y:z] = [m^2-n^2:2mn:m^2+n^2]$ とおける。
$C_i$上の点$[x:y:z]$に対して、それを通るような$[s:t]$が1つだけ定まる。
（$[s:t]$が1つに定まらない点が$\mathbb{P}^2$には一般に4点あるが、$C_i$はそれらを避けているとしている。）
今回の直交双曲線族の例では、$[s:t] = [z^2:xy]= [(m^2+n^2)^2: (m^2-n^2)(2mn)]$ である。

そうすると、$\mathbb{P}^1$から$\mathbb{P}^1$への次数4の写像$[m:n]\to [s:t]$が定まっている：
ほとんどの$[s:t]$に対して、それを与える$[m:n]$は4点あるが、
いくつかの$[s:t]$に対しては、それを与える$[m:n]$が4点より少ない。（「分岐点」）
それが求めるものである。
リーマンフルヴィッツの公式を使うと、分岐点は6点であることが分かる。

より地に足がついた観察では、
$t/s$ = ($m,n$の4次式)/($m,n$の4次式) という形をしているので、
非斉次化して考えると、$s=1,n=1$とおいた「($t$の1次式)係数な、$m$の4次方程式」が重解を持つ条件として、
4次式の判別式は係数の6次式であることから、$t$の6次方程式を得るというふうに納得できた。

なお、今回の具体例では、
$[s:t]=[2:1]$ で2重解が2つ（2点で接する）
$[s:t]=[2:-1]$ で2重解が2つ（2点で接する）
$[s:t]=[0:1]$ のとき2重解が2つ
という状況で、分岐点が重複度を込めて6点となっている。

$[s:t]=[0:1]$ のときは、直交双曲線は退化して「2重直線」$z^2=0$ となっている。
これが$x^2+y^2=z^2$と2つの「無限遠点」 $[1:±i,0]$ で2重に交わっているという解釈である。
▲▲

円$C:x^2+y^2=z^2$ に接する2次曲線の集合と、$x$軸と$x=-4,2$で交わる円の族 $x^2+2xz+y^2+tyz=8z^2$ の交わりを考える。
交叉理論によると、$\mathbb{P}^5$における6次超曲面と直線の交叉なので、交わりは6点存在するはずである。
$t=\pm 3\sqrt{5}$で2つの円は接するが、他に2つの円が接するときはなく、一見、交わりは2つしかない。

計算すると、$t=\pm 2i$のときに接している。
これを観察するには、$x\neq 0$のアフィンを考えて、$(Z,Y)=(z/x,iy/z)$平面にプロットすると良い
$1-Y^2=Z^2$ と $1+2Z-Y^2-itYZ=8Z^2$ としてプロットされる。
$t=2$のとき $(Z,Y)=(0,1)$で接し、$t=-2$のときに $(Z,Y)=(0,-1)$で接することが観察できる。


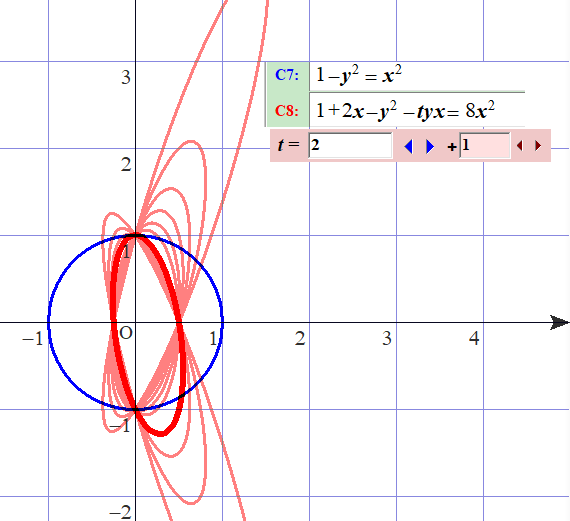
それでも、2点足りない。これは$\mathbb{P}^5$において、6次超曲面と直線が、$t=\pm 2i$で接していることによる。
これには、$C$に接する2次曲線の集合がなす6次超曲面の、点$C'$(つまり特定の2次曲線)における接平面を描写する必要がある。
事実としては、$C$と$C'$が1点$p$で接する場合には、$p$を通る2次曲面がなす超平面が、この接平面である(資料の補題8.5)。
上記の$t$でパラメータづけられた2次曲線族は$t$によらず常に点$(Z,Y)=(0,\pm 1)$を通るから、
$\mathbb{P}^5$においてこの族がなす直線は、接平面に含まれていることが納得できた。
・・このように具体例を、交叉理論から期待される数と一致させるように解釈するのはしばしば難しい。
▲▲

直積位相の視点から、略式に、
$t \neq 0$では滑らか2次曲線の族$A(t)$が、$t=0$では滑らかでない2次曲線になるときの
$(\lim_{t\to 0}A(t), \lim_{t\to 0}A(t)^*) \in \mathbb{P}^5 \times \mathbb{P}^{5*}$ が$X-U$に属することになる。

[例] 異なる2直線に近づく滑らかな双曲線の族$y^2-x^2=t$、正確には$X^2-Y^2+tZ^2=0$を考える。
双対曲線は、$\{[S:T:U] \in \mathbb{P}^{2*}; tS^2-tT^2+U^2=0\}$ となる。$t\to 0$では二重直線$U^2=0$となる。
この二重直線の双対な点[X:Y:Z]は、双曲線の漸近線の交点となっている。

[例] 二重$x$軸に近づく滑らかな楕円の族$y^2=t(x^2-1)$、正確には$tX^2-Y^2-tZ^2=0$の場合、
双対曲線は、$\{[S:T:U] \in \mathbb{P}^{2*}; S^2-tT^2-U^2=0\}$ となる。$t\to 0$では二直線$(S+U)(S-U)=0$となる。

[例] 二重$x$軸に近づく別の滑らかな楕円の族$y^2=t(x^2-t)$ の場合、正確には$tX^2-Y^2-t^2Z^2=0$の場合、
双対曲線は、$\{[S:T:U] \in \mathbb{P}^{2*}; tS^2-t^2T^2-U^2=0\}$ となる。$t\to 0$では二重直線$U^2=0$となる。

・このように2次曲線の族$A(t),B(t)$があるときに
$\lim_{t\to 0}A(t) = \lim_{t\to 0}B(t)$ であっても、それが二重直線のときには
$\lim_{t\to 0}A(t)^* = \lim_{t\to 0}B(t)^*$ とは限らない。

より詳しくは、$\lim_{t\to 0}A(t)$ が特定の二重直線$2L$になるとき、
$\lim_{t\to 0}A(t)^*$ の取り得るものは、2点$p_1,p_2 \in L$を選ぶだけの自由度がある：

一方で、$\lim_{t\to 0}A(t)$ が滑らかな直線や異なる2直線になるときは、
$\lim_{t\to 0}A(t)^*$ の取り得るものは、1つしかない。▲▲

2次曲線 $ax^2+2bxy+cy^2+2dxz+2eyz+fz^2=0$ に対して、
行列$m = \begin{pmatrix} a& b& d\\ b& c& e\\ d& e& f \end{pmatrix}$ を対応させる。
この行列の階数が3のときに滑らかな2次曲線
この行列の階数が2のときに異なる2直線
この行列の階数が1のときに二重曲線
となる。

双対曲線$AX^2+2BXY+CY^2+2DXZ+2EYZ+FZ^2=0$ に対しても同様に、
行列$M = \begin{pmatrix} A& B& D\\ B& C& E \\ D& E& F \end{pmatrix}$ を対応させる。
$X$は、これらの行列の積が単位行列に相当することを示す以下の8個の方程式で切り取られる。
$aA+bB+dC = bB+cC+eE = dD+eE+fF$,
$aB+bC+dE = 0,aD+bE+dF = 0,bD+cE+eF = 0$,
$bA+cB+eC = 0,dA+eB+fC = 0,dB+eC+fE = 0$

余次元5のものを切り取るのに8個の方程式があるのが、[寄り道1-1]の状況である。
5個の方程式だけでは、余計な成分もついてきてしまうのである。

[3-1]に描写した(a)(b)(c)(d)の関係については：
行列$m$のすべての$2 \times 2$小行列式が0である条件が、(b)∪(d)に相当する4次元閉部分多様体を切り取る。
行列$M$のすべての$2 \times 2$小行列式が0である条件が、(c)∪(d)に相当する4次元閉部分多様体を切り取る。
それらの交わりが、(d)に相当する3次元閉部分多様体となる。
▲▲