[1] 被覆射について 被覆射についての基本的っぽい練習問題が自分では解けず、適当に教材を探した。 https://ium.mccme.ru/postscript/s16/topology1-Lec11.pdf 補題11.1 道の持ち上げ 被覆射p:E→Bがあるとき、Bの道はEの道に持ち上がり、始点の持ち上げを指定すれば一意的である： 任意のα:[0,1]→Bと x_0∈p^-1(α(0)) に対して、α~:[0,1]→Eがあってα~;p;=αかつα~(0)=x_0となる。 [説明] 任意のb=α(t), t∈[0,1]に対して自明化近傍U_bが存在する。 U_bたちはαの像を被覆する。 ここでαの像はコンパクトなので（コンパクト空間の連続写像の像はコンパクト） 有限個のU_bがαの像を被覆する。 それぞれの自明化近傍で、αの像は持ち上げてつなげれば良い。 ・注意：閉路の持ち上げが閉路とは限らない。 （例えば円周から円周への2重被覆では、1周の持ち上げは半周） 定理11.2 ホモトピーの持ち上げ Bのホモトピーは、始写像の持ち上げが存在すれば、Eのホモトピーに一意的に持ち上がり、 始写像の持ち上げを指定すればその持ち上げは一意的である。 任意の F:A×[0,1]→B, f_0(・)=F(・,0) に対して、f_0の持ち上げf_0~を指定できれば、 F~:A×[0,1]→Eがあって、F~;p;=F かつ、F~(・,0)=f_0~(・) となる。 ・注意：始写像の持ち上げは存在するとは限らない。 （例えば先の円周から円周への2重被覆の例。） ・注意：被覆射ではない全射では持ち上げが一意的とは限らない。 [説明] 各α∈Aごとに、道を持ち上げる。 これが連続写像であることの確認がよく分からなかった・・。 https://math.stackexchange.com/questions/3610605/homotopy-lifting-property-for-covering-spaces 例えばwikipediaではAは path connected and locally path connected であることが要求されている。 系：基本群の誘導π_1(E)→π_1(B)は単射である。 定理11.3 Bが「局所的に良い」性質を持てば、基本群π_1(B)の任意の部分群Gに対して、 被覆射X→Bで、π_1(X)→π_1(B)の像がGであるようなものが一意的に存在する。 「局所的に良い」：局所弧状連結かつ局所単連結 （それぞれそうでない例が文献に書いてある） [説明] 始点と終点が一致する2つの道α,α'に対して、 αとα'の逆をつなげたループが、Gに属するときにα～α'と定める。 b_0∈Bを起点としたpath spaceを考える。P(B,b_0)とおき、商空間X=P(B,b_0)/～を考える。 p:X→Bを、pathの終点で定める。これが目的のものになる。 ・Xの位相 ・pが連続であること ・基本群の像がGであること ・pが一意的であること を確認する必要がある。(スキップ・・) 練習 ・11.1 n重被覆Y→Xがあるときのオイラー標数の関係は何か：χ(Y)=n*χ(X)
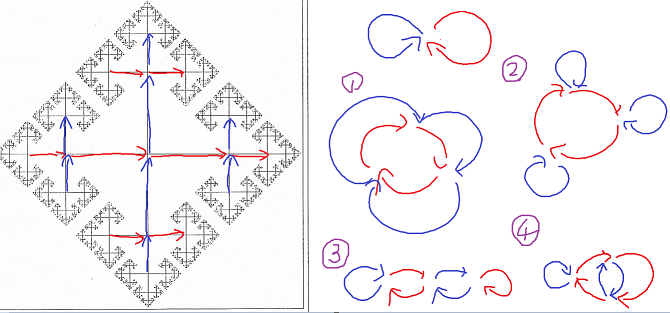
[2] 8の字 https://www.math.kyoto-u.ac.jp/~konishi/ex-geometry2014/fundamental-group.pdf 8の字の基本群は、生成元2つの自由群である 8の字の弧状連結な3重被覆をすべて求めよ： ・弧状連結 ・交点が3つ ・赤矢印と青矢印が3つずつ ・各交点に、出る赤矢印・出る青矢印・入る赤矢印・入る赤矢印が1つずつ を満たす図形を描くことに相当する。 ・①②③④の図を描いた。 ・①の青矢印の向きを変えたもの。 ・②の赤と青を変えたもの ・④の赤と青を変えたもの
普遍被覆の絵は、次のページで紹介されていたのを使わせてもらった。
https://math.stackexchange.com/questions/354056/universal-cover-of-a-figure-eight
3重被覆をYとして、8の字をXとする。
Yの基本群は、Xの基本群に単射される。単射される先を調べた。
これをまた、「基本領域の塗分け」として描写した。
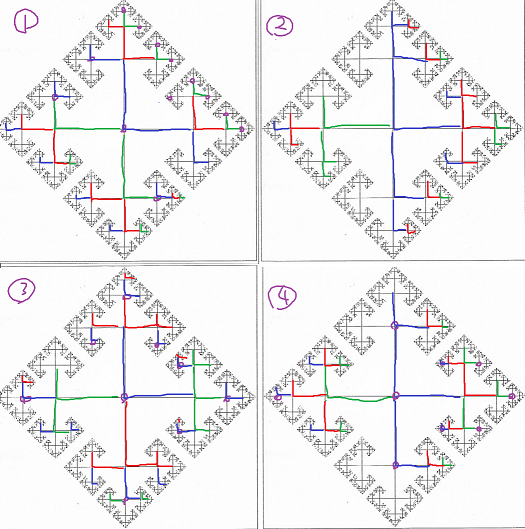単射される先はF_2の指数3の部分群をなす。
F_2の生成元をA,Bとして、逆元をa,bで表記する。
① (AAA,AAB,ABA,BAA)による自由群：(大文字)-(小文字)が3の倍数
①' ①のBをbに変えたもの。
② (AAA,B,ABa,aBA)による自由群：Aの個数が3の倍数
②' ②のAとBの役割を入れ替えたもの
③ (AA,BB,ABA,BAB)による自由群 [1,A,B]が剰余類の代表元となる
④ (AAA,B,ABA,AbA)による自由群 [1,A,AA]が剰余類の代表元となる
④' ④のAとBの役割を入れ替えたもの
・補足
生成元が4つなのは、Yの基本群に由来する（穴が4つある形をしている。）
①について、他の3文字の語は、例えば次のように、生成されることが確認できる。
ABB = ABA aaa AAB
BAB = BAA aaa AAB
BBA = BAA aaa ABA
BBB = BAA aaa ABA aaa AAB
[3] C-{0,1}の普遍被覆 ・https://mathoverflow.net/questions/807/describing-the-universal-covering-map-for-the-twice-punctured-complex-plane それは上半平面で、具体的な被覆はλ関数というものらしい。 ・https://mathoverflow.net/questions/29700/generators-for-congruence-group-gamma2 の回答のhereと書かれたリンク先： https://qchu.wordpress.com/2010/03/12/fractional-linear-transformations-and-elliptic-curves/ を読むと、楕円関数との関連が書いてあり、興味深く感じたので、自分の言葉で書いた。 [a] 楕円曲線は、y^2 = (x-a)(x-b)(x-c)の方程式で記述できる。(a,b,cは異なる複素数) y^2 = (x-a)(x-b)(x-c)と y^2=(x-a')(x-b')(x-c')はいつ同型になるか： 1次変換f(z)=(Az+B)によって集合{a,b,c}が集合{a',b',c'}に移るようなA,Bが存在するとき [b] 一方で、τ∈上半平面を使って、Λ=<1,τ>による格子で割ったトーラスC/Λとも記述できる。 <1,τ>によるものと<1,τ'>によるものはいつ同型になるか： g(z)=(Az+B)/(Cz+D), [A,B,C,Dは整数でAD-BC=1で、g(τ)=τ']となるようなA,B,C,Dが存在するとき [a1] 1次変換で(a,b)を(0,1)に移すことができるので、y^2=x(x-1)(x-λ)で記述できる。(λ∈C-{0,1}) y^2=x(x-1)(x-λ)とy^2=x(x-1)(x-λ')はいつ同型になるか： 1次変換によって、(0,1,λ)が(0,1,λ')の並び替えに移るようなとき。並べ替えは6種類なので6種類あって： λ'∈{λ,1/λ,1/(1-λ),1-λ,(λ-1)/λ,λ/(λ-1)} [a2] 楕円曲線と、2等分点の順番を指定したものは、y^2=(x-a)(x-b)(x-c) と {a,b,c}の順番指定で記述できる。 ということは y^2=x(x-1)(x-λ)で記述した場合は、λ∈C-{0,1}で特定できる。 [b2] 楕円曲線と、2等分点の順番を指定したものは、格子と、2等分点{1/2,τ/2,1/2+τ/2}の順番指定で記述できる。 <1,τ>によるトーラスに (1/2,τ/2,1/2+τ/2)の順番指定したものと、 <1,τ'>によるトーラスに (1/2,τ'/2,1/2+τ'/2)の順番指定したものはいつ同等になるか： g(z)=(Az+B)/(Cz+D), [行列[A,B],[C,D]∈Γ(2)で、g(τ)=τ']となるようなA,B,C,Dが存在するとき ・Γ(2)とは [[A,B],[C,D]]≡[[1,0],[0,1]] (mod 2) という合同部分群を意味している。 z∈Cのトーラスで与えられた楕円曲線 C/Λ への像は、 ワイエルシュトラスのペー関数p(x)によって、 y^2=4x^3-Ax-B 上の点 (x,y) = (p(τ,z),p'(τ,z)) に対応する。 p(τ,1/2), p(τ,τ/2), p(τ,1/2+τ/2) が、x軸との交点a,b,cと結びつく。 逆に、y^2=4x^3-Ax-B上である種の楕円積分をすると、τを復元する。 http://searial.web.fc2.com/aerile_re/theta.html の(2) 例えばp(τ,1/2), p(τ,τ/2), p(τ,1/2+τ/2)をこの順に(a,b,c)として、 (a,b)を(0,1)に移す1次変換によってcが移る先をλとする。 これによって、写像 C→C-{0,1} : τ→λ が定義される。 これが、目的の普遍被覆となるのである。 --- 被覆変換群は、Γ(2)であり、これは2つの生成元からなる自由群である。 （C-{0,1}は位相的に8の字と同じである。） モジュラー群の言葉を使うと、生成元には、 A = TT = [[1,2],[0,1]] と B = TSTTST = [[1,0],[2,1]] をとることができる。 基本領域には、{1,T,S,ST,STST,TST} をとることができる。(図の紫。)
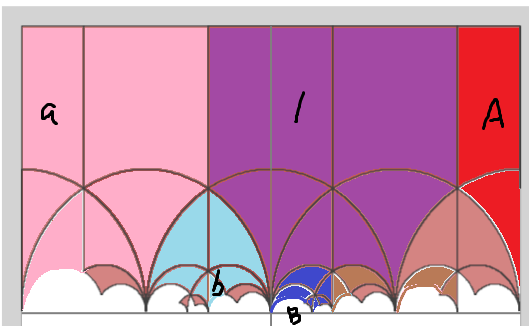（参考：基本領域ゲーム）
[余談] ピカールの小定理
被覆射：H→C-{0,1}が存在することは、ピカールの小定理を示すのに使われる：
「C から C-{0,1} への正則写像は定数写像しかない」
次のページのMatt E氏による2番目の回答参照：
https://math.stackexchange.com/questions/63401/picards-little-theorem-proofs
t.b.氏による別の技巧的な証明も紹介されていて興味深い。
2020/4/26
・追記。
Γ(2)からΓへの分岐被覆についてリーマンフルヴィッツの公式を観察してみた
2020/5/2