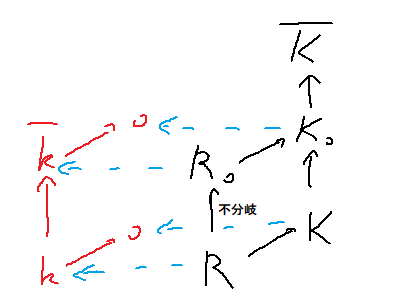
矢印は環準同型の方向で、スキームの射は逆向き、制限写像の向きは矢印と同じになる。
黒い矢印方向の、有限次元の中間体への射が、エタール射である。
（エタール射は、この場合、大まかに、不分岐で有限であると認識しておけば良い。）
＊Spec Z_5(√-3)→Spec Z_5は不分岐であるが、Spec Z_5(√5)→Spec Z_5は分岐する（のでエタールでない）。
＊一方、Spec Q_5(√5)→Spec Z_5は（像に閉点(5)が居ないので）「不分岐」で、エタールである。
水色の矢印は、Speck→SpecRによるbase changeの結果を示している。
具体的には、R上の環Sに対して、kとSのR上のテンソル積をとることになる。
実質的には、pで生成されるイデアルで割った剰余環をとることに相当する。
そういうわけで、不分岐性によって、R→R0のbase changeの結果は、離散付値環としての剰余体となる。
一方、Kのbase changeでは、pで生成されるイデアルは体全体なので、base changeの結果は零環となる。
これは、Speck→R←SpecKは集合的な意味で像が交わらないので、ファイバー積が空となるとも理解できる。
（A→X←Bのファイバー積は、集合的にはA∩Bとなる・・と思う。）
----
結果（このノートの内容の紹介）
[A] SpecR上のエタール層の圏は、次の(M,N,φ)の組の圏に同値である：
MはGK加群
NはGk加群
φは、Gk加群としての射N→τM
τMは、Mのうち、Ginで不変な部分群
この構成のことを、資料では、τのmapping cylinderの圏と呼んでいる。
（この幾何的な用語のモチベーションはよくわからない。）
GK加群の圏からGk加群の圏への関手としてのτは左完全である。
この結果を、茎の言葉でも略式に描写することもできた。
このあたりについて、理解できた範囲で説明したい。
[B] 閉埋め込みj:Speck→SpecRと、開埋め込みi:SpecK→SpecRに対して、
6つの関手j!, j*, j*, i*, i*, i! がある。
これは層の演算として本で読んだことが有ったが今回のような具体例を扱う機会がなかなかなかった。
[Mazur]では、これらの演算を、上記のmapping cylinderの(M,N,φ)を使って記述している。
そのあたりを観察した。
特に、j!とi!については、実数上の連続関数の層の場合も観察し、馴染みを増やした。
[C] エタールコホモロジーの計算（最初は書かないつもりだったがやっぱり書きたくなった）。
特に、N=K￣*, M=U0で描写されるエタール層のコホモロジーを目標としている。
それからその後のモチベーションを少し。
[1] 体SpecK上のエタール層は、茎で決まり、その結果GK加群と同等である。 [1-1] ・まずK上のエタール層Fと、有限次ガロア拡大L/Kでの状況を描写する。 σ∈Gal(L/K)をとる。σ(L)によって、群の圏での同型射F(L)→F(L)が引き起こされる。 これを、F(L)へのσの作用として解釈する。 （一度分かってしまうとこれだけなのだが、これを納得するにはかなり時間がかかった。） 例えばL/Kが2次拡大でF(L)が位数3の巡回群{1,ω,ω2}のとき、 σはωをωに送る場合と、ωをω2に送る場合が考えられる。 ・このとき、Fがエタール層であるという条件から、 K上の切断は、L上の切断のうちGal(L/K)で固定されるものと同一視されることが要求される。 σがωをωに送る場合は、F(K)も位数3の巡回群、 σがωをω2に送る場合は、F(K)は単位元のみ、ということになる。 -- ・この状況を、具体的な環準同型で観察することを試みた。（あまり自信がない。） C/R = 複素数体/実数体 という2次拡大を例にした。 一般に、L＠Lは、ガロア群の元で添え字づけられた個数のLの直積となる。 （[Stacks]「茎へのガロア群の作用」https://stacks.math.columbia.edu/tag/03QW） 前回のノート（エタール層Z/nZとμ_nについて）の[3]代数的な寄り道でも見た。 L＠Lから各成分への環準同型は、x＠yを、xσ(y)に移すものとして記述することができる。 このときx側を固定した時の、y側の行先を見ることで、ガロア群の作用を見ることができると解釈した。 R[x]/(x2+1)＠R[y]/(y2+1) = R[x,y]/(x2+1,y2+1) = R[x,y]/(x2+1,y-x)×R[x,y]/(x2+1,y+x) = R[s]/(s2+1)×R[t]/(t2+1)
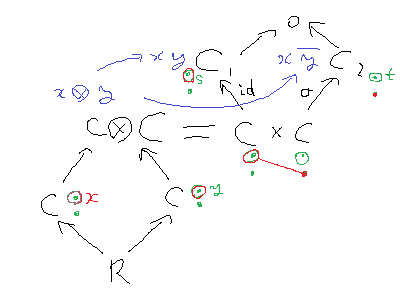左下のCと右上のC1,C2を同型で結ぶ。ここでは、x=s=tとこの同型を設定する。
そうすると、xは (s,t), yは (s,-t)に対応する。
例えばC自体をC上の切断とした場合には、yの第二成分の符号が変わるということは、
ガロア共役がxを-xに送ることに相当していると解釈した。
・この場合は「xとyがC＠Cの異なる元に送られる」という事実が、
略式に、「共通部分への制限写像の行先が異なる」と解釈され、
従って層の貼り合わせ公理を満たさないのでRの切断を与えないと解釈できる。
（この類似が成り立つことの背景にある仕組みは十分に理解していない。）
一方、ガロア群が自明に作用するものは、C＠Cの同じ元に送られ、Rの切断を与える。
[1-2]
・これを積み重ねることを考えれば、絶対ガロア群GKが作用するアーベル群F_sを与えておけば、
中間体Lに対しする切断を、L/Kを固定する部分群G_Lが固定するF_sの部分群によって定めてエタール層を得る（と思う）。
＊K上のエタール射は、中間体のスキームからの射だけではない。
例えばK=Q_5の場合、Q_5×Q_5や、Q_5(√-3)×Q_5(√5)などもQ_5に注ぐエタール射を与える。
しかし、Fが層であるという条件から、F(Spec L×L')はF(SpecL)×F(SpecL')で与えられる。
せっかくなので念のため説明：
SpecL → SpecL×L' ← SpecL' のファイバー積は零である。
これが略式に、共通部分が空である、共通部分への制限は常に一致する、
従って任意の(Lの切断, L'の切断)の組は共通部分への制限が一致するので貼り合わさって、
それぞれSpecL×L'の切断を与える。
・一方で、エタール層があるときに、上記の方法でガロア群の作用を定め、
K￣へ至る切断の帰納極限をとる操作（茎をとる）で、絶対ガロア群が作用するアーベル群F_sを得る（と思う）。
・茎をとる関手は、SpecK￣→SpecK (エタール射ではない) による層の引き戻しとも解釈できる。
（SpecK￣→U→SpecKと経由するエタール射U→SpecK上の切断の帰納極限）
[2] SpecR上のエタール層 冒頭の設定に戻る。 SpecK上のエタール層の圏 = GK加群Mの圏 Speck上のエタール層の圏 = Gk加群Nの圏 SpecR上のエタール層の圏 = 冒頭に述べた(M,N,φ)の組のなす圏（この等号は未知だけど） M:GK加群、N:Gk加群、φ:Gk加群の準同型N→τM、τM:MのうちGinで固定される部分 以下環上の切断F(Spec(A))のことを、Specを省略してF(A)と略記する SpecRのエタール層Fを定めるには、以下を定めれば良い。 K⊂K'をいろいろな有限次拡大として、 ・K'の整閉包をR'として、R'→Rが不分岐ならば、F(R'),F(K')および、「制限写像」F(R')→F(K')を定める ・K"の整閉包をR"として、R"→Rが分岐するならば、R"→Rはエタールでないので、F(K")だけを定める ・それらの間の制限写像 他のエタール射[例えばQ_5(√-3)×Q_5(√5)]での切断は、先のように直積であることが勝手に要求される。 以下、K'は付値に関して不分岐、K"は付値に関して分岐する有限次拡大体として使う。 ここで、F(R')たちを定めることは、 対応する剰余体k'上の切断をG(k')=F(R')とするような、 Rの剰余体k上のエタール層を定めることと同等であるという観察がある。 k'← R'← K' ↑ ↑ ↑ k ← R ← K → K" そういう事情で、[1]の結果と合わせて、 F(R')たちを定めることが、Gk加群Nを与えることに相当し、 F(K'),F(K")たちを定めることが、GK加群Mを与えることに相当し、 その間の制限写像を定めることが、φを与えることに相当し、合わせて(M,N,φ)の組を与えることに相当する。 ・Mは、層Fの生成点η（上の幾何的点）における茎と解釈できた。 同様に、Nは、層Fの閉点p（上の幾何的点）における茎と解釈できる。 これは[1]の最後と同様に、Spec k￣→ Spec R (エタールでない) によるFの引き戻しとも解釈できる。 「pを含む開集合上の切断」の帰納極限である。（冒頭の水色の矢印） そういうわけで、R上のエタール層が(M,N,φ)の組で記述できることは、 「R上のエタール層はRの閉点と生成点に対応する2つの幾何的点の茎と、それらの間の制限写像的なもので決まる」 という仕組みだと解釈できた。 制限写像が登場するのは、閉点pが属する開集合には常に生成点ηも属するからである。
[3] 6つの関手j!, j*, j*, i*, i*, i! [3-1] (M,N,φ)での記述の結果をまとめて記載しておく： ・引き戻しi*: (M,N,φ) → N ・引き戻しj*: (M,N,φ) → M ・押し出しi*: N → (0,N,0) ・押し出しj*: M → (M,τM,id) ・0による拡張 j!: M → (M,0,0) ・閉点を台とする切断 i!: (M,N,φ) → kerφ ---- ・引き戻し：すでに言及した。 j:p→SpecRの引き戻しは「pを含む開集合上の切断」の帰納極限であった。 一般に、Y上の層Fがあるときの、X→Yによる引き戻しは、茎をそのまま引き戻す。 ・押し出し： X上の層Gがあるときの、X→Yによる押し出しは、V→Yの開集合上の切断を、 U→V ↓↓ X→Y というファイバー積U→Xに対するGの切断によって定める。 k上のエタール層Gがあるとき、それをiによって押し出したR上のエタール層Fは、 [2-1]の言葉でF(R')=G(k')で定め、F(K')=0, F(K")=0で定め、制限写像は零写像な層である。 これは、K'のiによる逆像が零だからである。 これを(M,N,φ)の言葉で書くと N→(0,N,0) ということになる。 ＊[Mazur]534ページ、表現可能でないエタール層の例として、μ_nのiによる押し出しがあった。 F(R')はRのn乗根、F(K')やF(K")は自明な群、という層である。 K上のエタール層Gがあるとき、それをjによって押し出したR上のエタール層Fは、 F(R')=G(K'), F(K')=G(K'), F(K")=G(K")で定めるものである。 これは、R'のjによる逆像は、Kのjによる逆像と同じだからである。 誘導されるF(R')たちは、Gk加群の構造となるが、これが、 GK加群Mのうち分岐する所の情報を捨てたもの、すなわちτMである。 これを(M,N,φ)の言葉で書くと M→(M,τM,id) ということになる。 ---- ・(開埋め込みに関する)0による拡張j! X上の層Gがあるときの、開埋め込みX→Yによる0による拡張は、V→Yの開集合上の切断は、 V ↓ X→Y と経由するような切断からなる前層を層化したものとして定義される。 O_X加群においては、j!に相当するような、生成点での摩天楼層は、準連接層ではない。([Vakil 13.2.A]) そういう事情で、代数幾何ではj!はあまり登場しなかったんだと思う。 通常の位相での層でイメージを観察する[Vakil 2.7.G] R上の通常の位相での、連続関数の層を考える。 開集合(0,2)上の連続関数の層Gを、開埋め込みに関して0による拡張をした層F=j!Gを考える。 層化するまえの前層を、j!preGとおく。 開集合(1,3)上のj!preGの大域切断は空である。 これはこの開集合が(0,2)に収まっていないからである。 ところが、(1,3)上のj!Gの大域切断は空でなく、(1,2)の外では0となる連続関数である。 ・j!Gの点y∈Yにおける茎は、y∈XのときGの茎と同じで、そうでないとき0である。 ・自然な層の準同型 j! j* F → F が存在する。 ・開集合X→Yの補集合をZとして、閉埋め込みZ→Yをiとおく。 層の完全列 0 → j!j*F → F → i*i*F → 0 がある。 これは、 j!j*Fは開集合XだけでFと同じ茎を持ち、 一方で、i*i*F は閉集合ZだけでFと同じ茎を持つからである。 R上のエタール層の話に戻る。 K上のエタール層Gがあるとき、それをjによって0で拡張したR上のエタール層F=j!Gは、 F(R')=0, F(K')=G(K'), F(K")=G(K") で定まる。 ここで、実数の場合と違って、層化をしてもF(R)が増えないことは、自明ではないと思う。 これは閉点pを含む任意の開集合が、開埋め込みされた生成点ηを丸ごと含んでしまっているからである。 これを(M,N,φ)の言葉に翻訳すると、確かにMを(M,0,0)に移すことになる。 ---- ・閉点を台とする切断 i!: (M,N,φ) → kerφ https://en.wikipedia.org/wiki/Exceptional_inverse_image_functor iが局所閉埋め込みX→Yの場合は、Y上の層Fに対して、X上の層i!Fは、 「Xの外では0となるような切断からなる層」として定義される。 先の実数上の連続関数の層の例を使うとイメージが観察できた。 閉集合[0,2]のRへの埋め込みをiとすると、 i!Fは、両端で0になるような[0,2]上の連続関数からなる部分層である。 R上のエタール層に戻る。R上のエタール層Fがあるとき、 i!Fは、制限写像F(R')→F(K')の行先が0であるような切断からなる層である。 そういうわけで、(M,N,φ)の言葉では、確かにkerφということになる。 -------- [4] 完全性と随伴性 以下SpecR上のエタール層(N,M,φ)の組を、NとMの2行で表すことにする。 [4-1] (M,N,φ)の圏の完全列は、NとMについてそれぞれ完全であることを意味する（と認識している）。 ・[2]のj!の所で少し言及した 0 → j!j*F → F → i*i*F → 0 に相当する完全列は、 0→0→N→N→0 0→M→M→0→0 ---- [4-2] i*, i*, j*, j!は完全、j*,i!は左完全 ・例えばj!が完全であることは、 N → N'→N" M → M'→M" が完全ならば、j!で移した列 N → N'→N" も完全であることを言っている。 ・j*が左完全だけなのは 0→M → M'→M"→0 が完全であるときに、 0→τM → τM'→τM"→ ？ 0→ M → M' → M" → 0 の？の部分が0になるとは限らないことによる。(τが左完全だけだから。) 資料の525ページに書いてあるRqj*Gm,R = (RqτGm,R, 0,0) はこの図式の内容である。 ・i!が左完全だけなのは、 0→N → N'→N"→0 0→M → M'→M"→0 が完全の時に、 0→ker(N→τM)→ker(N'→τM')→ker(N"→τM")→？ が右完全にならないからで、 これは蛇の補題で、→coker(N→τM)→coker(N'→τM")→coker(N"→τM")→0 と続く。 そういうわけでi!の1次右導来関手がcokerで、2次以上の右導来関手が消えることも観察できる。 資料の先の所の次に書いてある、 Rq i! Gm,R = 0 (q≠1), Z (q=1) という事実はこの視点から納得することができる。 [ Gm,Rは(N,M)=(U0,K￣*)という組であった。 ] ---- [4-3] 随伴関係：j! -| j* -| j*, i* -| i*, i! 例えば随伴 j! -| j* は、Hom(N,N') と Hom( (N→M) → (N'→0) ) が自然に全単射になることを言っている。 N → N' ↑ ↓ N → N' M → 0 左の縦矢印がj!で、右の縦矢印がj*である。（j!が左随伴、j*が右随伴。） 他の組も同様に観察できる。 より一般な設定でもj!とj!が定義されて互いに随伴であり、 今回の設定では、j!=j*, i!=i* という状況らしい。 https://en.wikipedia.org/wiki/Image_functors_for_sheaves
[5] コホモロジー [5-1] 定義 R上のエタール層F=(M,N,φ)に対して、コホモロジーHq(R,F) = Ext(Z,F) = RqΓ(F)で定める。 これは、Fに対して、射(Z,Z,id)→(M,N,φ)の集合がなす群を返す関手Γ(F) = Hom(Z,F) を考えて、 その右導来関手を考えるというものである。 ・「右導来関手」の言葉には以前は読み飛ばしたくなるような抵抗があったが、 左完全関手α=α0の右導来関手αqとは、 完全列 0→F→G→H→0 に対して 0→α0(F)→α0(G)→α0(H)→α1(F)→α1(G)→α1(H)→α2(F)→.. を成り立たせるα_qとして理解してしまえば実用的には十分であることに気がついて、だいぶ抵抗が減った。 （ここからはG,Hの取り方によらずα_q(F)が定まることなども分からないけど、それが定まる仕組みが裏にあるとだけ理解している。） ・Hom(Z,F)が、Rでの切断をとることと同等である。 このZ（資料では太文字）は定数層を意図している。 層準同型Z→Fを定めるとき、すべてのエタール射U→Rに対して、Z(U)→F(U)を一貫性のあるように定める。 特にUとしてR自体を考える。Z(R)=Zの生成元1が、「大域切断」F(R)のどの元に送られるかを定める必要があり、しかし、それで十分である。 なぜならそれを定めてしまえば制限写像によってZ(U)=Zの生成元の行先は、今定めた元を制限したものに決まるからである。 そういうわけで、「Rの大域切断を1つ選ぶ」のと同じである。 ・もう1つ、コンパクトコホモロジーというのを定義している。Hcompq(R,F) = Ext(i*Z,F) と定義している。 これは、先と同様に、「Rの大域切断のうち、Kへの制限写像で0に移るようなものを1つ選ぶ」と解釈できる。 [Mazur]ではこれも後から種明かしをしていたが、これは相対コホモロジーの概念で、[5-3]でその視点を書いた。 [Mazur]のTateの双対を得るという目的を果たすにはこちらのコホモロジーが必要だったということらしい。 ---- [5-2] 計算 次のSpecR上のエタール層の完全列がある。 0→U0→K0*→Z→0 0→K￣*→K￣*→0→0 この左辺のエタール層をGm,R K上の可逆元による乗法群からなるエタール層をGm,Kと定義する。 完全列は、0 → Gm,R → j* Gm,K → i*Z → 0 と描写される。 （Gm,Kの幾何的点での茎K￣*のGin不変部分がK0*なので、先の記述と一致する。） [Mazur]の議論は、この完全列を利用して、 残り2つの項のコホモロジーを計算することで、Gm,Rのコホモロジーを計算している。 ・R上のj* Gm,K のコホモロジーは、K上のGm,Kのコホモロジーと同じである これは、自明ではない。 j*の右導来関手は、τの右導来関手で記述できることを[4-2]で見た。 Gm,Kに対しては、τの右導来関手の結果が消えることがポイントのようである。 この事実は、群コホモロジーとしては、Gの惰性群のコホモロジーHq(Gin,K￣*)が消えることに対応する。 「すべての正の次元のガロアコサイクルは、不分岐拡大でコバウンダリになる」という事実に対応する。 これは[Mazur]では局所類体論から得ると書いてあるが、 局所類体論の結果をガロアコホモロジーの言葉で記述する視点が私にはまだよくわからなかった。 ・改めて、K上のGm,Kのコホモロジーを考える必要がある。 これがまた、ガロアコホモロジーに相当する。(https://stacks.math.columbia.edu/tag/03QQ) 特に、0次コホモロジーは大域切断であり、これは[1]のように、GK加群Mのうち、GK不変な元を意味した。 （この様子からも、通常の群コホモロジーと同じことが観察される。） Gm,K=K￣* のガロアコホモロジーは、0次がKの乗法群K*、2次がQ/Z、他は自明という結果らしい。 この結果もまた、局所類体論から計算されると書いてあるが、私はまだ理解が十分でない。 （ブラウアー群からQ/Zへのinvariant写像とか呼ばれるものがあったような気がする程度の認識） ・もう1つの項、i*Zの項のコホモロジーは、0次がZ、2次がQ/Z、他は自明という結果らしい。 これは、今度はGkのほうのガロアコホモロジーとして、Hq(Gk,Z)に帰着する。 これは、0→Z→Q→Q/Z→0および、Hq(Gk,Q)が消えることから、 いわゆる「次元シフト」でH2(Gk,Z) = H1(Gk,Q/Z) = Hom(Gk,Q/Z) = Q/Z と得られる。 ・以上から、先の完全列のコホモロジーをとった長完全列は次のようになる 0→U0→K0*→Z →H1(R,Gm,R)→0→0 →H2(R,Gm,R)→Q/Z→Q/Z →H3(R,Gm,R)→0→0 これより、q＞0に対して、Hq(R,Gm,R)=0 である。 ・コンパクトコホモロジーをとった長完全列は次のようになる（導出省略） 0→0→0→Z →Hcomp1(R,Gm,R)→0→0 →Hcomp2(R,Gm,R)→0→Q/Z →Hcomp3(R,Gm,R)→0→0 これより、Hcomp1(R,Gm,R)=Z、Hcomp3(R,Gm,R)=Q/Zである。 Hqについては、一般の場合は、 ・H0(X,G_m)は単数群 ・H1(X,G_m)はピカール群（離散付値環では自明だった事情） ・H2(X,G_m)はブラウアー群 ということらしい。 [nLab] https://ncatlab.org/nlab/show/basics+of+etale+cohomology の最後の方に書いてあった。 ---- [5-3] 切除完全列 i:V→Xを閉埋め込みとして、Uをその補集合とする。 X上のエタール層Fのうち、XのうちV以外で0となる切断をとる関手をΓV(F)として、 これの右導来関手をHVq(X,F)と書く。 これは[Mazur]p.535で相対コホモロジー HVq(X,F) = Ext(ZV,F)と呼ばれている。 ..→HVq(X,F)→Hq(X,F)→Hq(U,i*F)→Hq+1(X,F)→.. が完全となる。 ([Mazur]でUの所がVになっているのはたぶん誤植だと思う) 今回の閉埋め込みi:Speck→SpecRでF=Gm,Rで適用すると、 ..→Hq(R,F)→Hcompq(R,F)→Hq(K,Gm,K)→.. となって、q=3まで書き出すと 0→U*→K* →Z→0→0 →0→0→Q/Z →Q/Z→0→0→.. を得る。（逆に、これによってどれかを逆算することもできたと思う）
[6] その先のモチベーション [Mazur]では、「米田ペアリング」を使って、「Tateの局所双対」を得ている。 それから、大域体についても同様のことができることを述べているようである。 大域体の場合は、 0→Gm,R→j*Gm,K→それぞれの閉点p上の定数層Zからの押し出しの直和→0 という完全列があるらしい。これのコホモロジーを考えると、 「大域Gm,Rの情報を、局所の情報と結びつけられる」・・ような気がする。 0→D*→K*→(直和)Z →H1→0→0 →H2→Q/Z→(直和)Q/Z →H3→0→0 結果は、Kが総虚である場合は、 H0は単数群R* H1はイデアル類群 H3はQ/Z 他は0 となるらしい。（Kが総虚でない場合は少し異なると書いてある。） この計算にはやはり類体論を使うと書いてある。詳細は追えていない。 [nLab]で引用されているMilneの資料を見た。（過去に眺めたことは何度かあったが読めなかった。） [Milne] https://www.jmilne.org/math/CourseNotes/lec.html そうすると、[2]までに今回理解したことは、 [Milne]では8章の"Sheaves on X=U∪Z"という項に書いてあった。 （しかし、これだけ読んでも今回のような理解は得られなかっただろう） また切除完全列については9章、G_mのコホモロジーについては13章に書いてあった。 そういうわけで、[Mazur]を読んで考察していたら、 期せずして、[Milne]の前半に相当する内容をある程度得た。 とりあえず、[Milne]の続きを少しずつ読み進められたら良いと思っている。 雑談 [Mazur]では、最初にエタール層に言及せずに(M,N,φ)の組とこれらの演算を記述し、 p.532で一般論を述べてExamplesとして種明かしをしている。 [Milne]では、逆に一般論を先に書いてある。 今回は[Mazur]の書き方が有難かったが、 読んでいる途中はどういう順番で何が書いてあるかよくわからず、何度も行ったり来たりした。 種明かしされると、最初からそう書いてくれれば良いのにという気持ちになったが、 しかし最初からそう書いてある[Milne]の書き方だと、それはそれで読めなかっただろうなとも思ったりした。 難しい。 2020/09/17
ノート一覧