�~���̂̃K���A�Q(2016/2/23) �~���̂́A�K���A�Q�̊T�O�Ɋ����̂ɂƂĂ��ǂ���ނ��Ǝv���B ���̃m�[�g�̖ڕW�́Ap/q�������Aq��3�ȏ�̎��R���Ƃ��� cos(2��p/q)�̍ŏ��������̎�������(q)/2�ɂȂ邱�� ���K���A�Q�Ɗ֘A�t���ďЉ�邱�Ƃ�ڎw�� �E�E�Ǝv���ď������Ƃ������̂� �G�ȏЉ���ł��Ȃ������B���ǂ�[*2]�Ƃ����ɏЉ�Ă�pdf���Q�Ƃ��Ăق��� [*1] http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13136585998 �ŏ���������3�����邢��4���������ɂȂ�ꍇ [*2] http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13150899098 cos(p��/q)���L���� ���p��Ƃ��� [*3] http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13129216628 cos(��/n)+cos(3��/n)+cos(9��/n) = a+b��d�@�ƂȂ�悤��n �ق��ǂ݂₷�����̂Ƃ��Ă͗L���ȏ��ł����u�����̂��������ہv�Ȃ� ----- * �́A�g��́A���ԑ� �u�́v�Ƃ́A�l�����Z�ŕ����W���ł���(0�Ŋ���̂�������) �L������Q���܂ށA�L�������傫�ȑ̂�����B ������R�╡�f����C�͂��̑�\�ł��邪 ����l�@����̂͂������͂�����"������"�̂ł���B �Ⴆ�� Q(i)�ƌĂ�� {a+bi|a,b��Q} �Ƃ����W���Ƃ� Q(��)�ƌĂ�� {a+b��|a,b��Q}, ��=(-1+��-3)/2 �Ƃ����W���Ƃ� �̂̐�������AK��̂Ƃ���x��K�Ȃ��x�̗L�����͑S��K�ɑ�����B ��ʓI�ɗL�����ɁA(Q�W����)����ȑ������̉�����Y��������Q(��)���l����̂��T�^�I�ł���B �i���̂悤�ȃ��͑㐔�I�Ȑ��ƌĂ�A�ŏ��������Ƃ������̂��l���邱�Ƃ��ł���B�j "�Y��"�Ƃ́A�������̈Ӗ��ő������A���l�ł���B �EQ�ƃ����܂ލŏ��̑� �E���̗L�����ŕ\�����W�� �E���̑������ŕ\�����W�� �i2�ڂ�3�ڂ̓��l��"����̗L����"�̖{���I�ȏ����Ǝv���j * Q��L �ƂȂ�̂�����Ƃ� L��Q�̊g��̂ƌĂԁB�iQ��L�̕����̂ƌĂԁB�j �@���̊g����K���I��L/Q�Ə����B * K��M��L �ƂȂ邻�ꂼ���K,M,L������Ƃ� M �͊g��L/K�̒��ԑ̂ƌĂԁB ��@����U�Y���ƁAQ�̊g���L�́AQ��́i�L�������́j���`��Ԃł���B ���̎����͊g�原���ƌĂ�� [L:Q] �Ƃ����ӂ��ɕ\�L�����B ����n���������̉���1����Y��������Q(��)�͊g�原����n�ł���B (1,��,��^2,...,��^(n-1)�͐��`�Ɨ��ł���Q(��)�̔C�ӂ̌��͂����̐��`�����ł���) ----- * �~���� 1�̌��nn�捪exp(2��/n)����n�Ƃ������Ƃ���Q(��n)���~���̂ƌĂ��B ���̂��ƓY������n�͓K�X�ȗ�����B n=1,2 �ł� �Ă͗L�����Ȃ̂� n��3 ��z�肷��B n=3,4 �̂Ƃ��͂��ꂼ���ɏЉ�� Q(��),Q(i)�̂��Ƃł���B [��] ������Q�̊Ԃɂ́A�ʂ̒��ԑ̂́A���݂��Ȃ��B [��] �Ⴆ��Q��M��Q(i)�Ƃ�����Q��M������M�� a+bi, b��0 �Ȃ錳�����B �@��������Ɛ�Ɏw�E�������Ƃ���M�� Q(i)�̌����ׂĂ������Ƃ�������B �En=5�̂Ƃ� Q(��)��Q�̊Ԃɂ͒��ԑ̂����݂���B�����Q(��5)�ł���B Q(��5)��Q(��)�̕�܊W�������łȂ���������Ȃ��B �� = (-1+��5)/4+��(-2��5-10)/4 ��^2 = (-1-��5)/4+��(2��5-10)/4 ��^3 = (-1-��5)/4-��(2��5-10)/4 ��^4 = (-1+��5)/4-��(-2��5-10)/4 ��+��^4 = (-1+��5)/2 ��� (-1+��5)/2 �� Q(��) ���m�F�ł���B ������C�ӂ� a+b��5|a,b��Q ���Ă̑������ŕ\����邱�Ƃ��]���B ----- �En=7�̂Ƃ� Q(��)��Q�̊Ԃɂ�2�̒��ԑ̂����݂���B Q(��-7) �� Q(cos(2��/7)) �ł���B �EQ(cos(2��/7)) �� Q(��)���������ȑ̂ł��邱�Ƃ́A cos(2��/7) �̍ŏ���������3�����ł��邱�Ƃ��番����B ���ۂɒ��ԑ̂ł��邱�Ƃ́F �E��+��^6 = 2cos(2��/7) �E��+��^2+��^4 = (-1+��-7)/2 ----- * �~���̂̃K���A�Q �K���A�Q�́A�g��ɑ��Ē�`�����B�����ł�Q(��)/Q�ɑ���K���A�Q���l�@����̂ł���B �yf(x+y)=f(x)+f(y), f(xy)=f(x)f(y)����Q(��)����Q(��)�ւ̑S�P�ˎʑ��z���l���邱�ƂɂȂ�B �ix��Q �̂Ƃ� f(x)=x �ł��邱�Ƃ���`��v������邪���R�ɖ��������j �i�K���A�Q�̌����m�ɁA�ʑ��̍����ɂ���ĉ��Z�����āA�Q�Ƃ݂Ȃ��B�j ���̂悤��f�ɂ��Ă̑��ɂ��āA����k�������� f(��) = ��^k �ƂȂ邱�Ƃ�������B f(��)�����܂�AQ(��)�̌��͂��ׂăĂ̑������ŕ\����邩��A f(x+y)=f(x)+f(y), f(xy)=f(x)f(y)�ɂ����Q(��)�̌��̍s���悪���ׂČ��܂�B �����ŁAk��n�ƌ݂��ɑf�ł���K�v������B�������Ȃ���f�����������Ȃ�(�S�P�˂ɂȂ�Ȃ�) �t�ɁAk��n�ƌ݂��ɑf�ł�����̎ʑ��͏��������B ���̏ؖ��͖{���I�ɉ~���������̊��ƊW���A�����ł͂Ȃ��Ǝv���B �Ă���^k �Ɏʂ��ʑ�����[k] �Ɩ��t���邱�Ƃɂ���B ������k��j (mod n) �̂Ƃ� ��^k=��^j�ł����[k]�ƃ�[j]�͓���ł���B ���Ȃ킿�Ak�́A�un��@�Ƃ�������]�ށv�Ǝv�����Ƃ��ł���B �܂��A�ʑ��̍����́A��[k]�E��[j] = ��[kj] �ŕ\�����B ���Ȃ킿�A������u�����]�ނ̂Ȃ���@�Q�vZ/nZ* �Ȃ̂ł��� ----- * �K���A�̊�{�藝���咣����ɂ́A���ԑ̂��ǂꂾ�����邩��m��ɂ� �@�K���A�Q�̕����Q���ǂꂾ�����邩��m��Ηǂ� (Z/5Z)* �� Z/4Z �ɓ��^�ł���A{0+4Z,2+4Z} �Ƃ��������Q�����B (Z/5Z)* �̕����Q�Ƃ��Ă� {1+5Z,4+5Z} �Ƃ��������Q�ł���B (Z/7Z)* �� Z/6Z �ɓ��^�ł���A{0+6Z,2+6Z,4+6Z}, {0+6Z,3+6Z} �Ƃ��������Q�����B (Z/7Z)* �̕����Q�Ƃ��Ă� {1,2,4}+7Z, {1,6}+7Z �Ƃ��������Q�ł���B ��+��^2+��^4 = (-1+��-7)/2 �̎w����1,2,4 �ȂǂƂȂ��Ă���̂͋��R�ł͂Ȃ� �E�K���A�Q�̕����Q������A�Ή����钆�ԑ̂�����B Q(��)/Q �̃K���A�Q��G�Ƃ����BG�̕����Q��H�Ƃ����B Q��M��L �ƂȂ钆�ԑ�M�̏W��X�ƁAG�̕����QH�̏W��Y�����̂悤�ɑΉ�����F M��X ---> Y = {g��G | �C�ӂ�x��X�ɑ���g(x)=x} H��Y ---> M = {x��L | �C�ӂ�g��H�ɑ���g(x)=x} �����M,H������őΉ����Ă���Ƃ� |H|=[L:M], |G|/|H|=[M:Q] �����藧�� ----- �En=7 �̏ꍇ�̏� Q(��)�̕����W���ŁAH3={��[1],��[2],��[4]} �̍�p�ŕs�ςȏW��������B �����M2�Ƃ����Ƃ���͑̂��Ȃ��A|G|=6, |H3|=3 �� [M2:Q]=2 �ł���B �t�ɁAQ(��)�̕����̂ł�����H3�̍�p�ŕs�ςȂ��̂�����A�����M2�̕����̂ł���B H3�ɑ����Ȃ�G�̌�(�Ⴆ��[3])�ŕs�ςłȂ���A�����M2�Ɉ�v����B Q(��+��^2+��^4) ��H3�̌��ŕs�ςł���B �Ȃ��Ȃ��[1]�͍P���ʑ��ł��邵�A ��[2] �� �Ă���^2�Ɏʂ��A��^2��(��^2)^2�Ɏʂ��A��^4��(��^2)^4�Ɏʂ��A ���ꂼ�� ��^2,��^4,�� �ƂȂ邩��A��[2](��+��^2+��^4) = ��^2+��^4+�� �ŕs�ςƂȂ�B ��[4] �����l�ł��� ���̂��Ƃ���܂� ��+��^2+��^4 ��Q��ŏ���������2���ȉ��ł��邱�Ƃ������� ��� ��[3] �̓�+��^2+��^4����^3+��^5+��^6 �Ɏʂ��A��+��^2+��^4�ƈقȂ�B ���̂��Ƃ��� ��+��^2+��^4 ��Q��ŏ��������͂��傤��2�����ƕ�����B ----- H={��[1],��[-1]} �ɑΉ����钆�ԑ̂� Q(cos(2��/n)) = Q(��+1/��)�ł���B ���������킯�ŁAcos(2��/n)�̍ŏ��������̎����́A|G|/|H| = ��(n)/2 �ł���B ----- [���K���] n=15�̏ꍇ�AQ��M��Q(��)�ƂȂ钆�ԑ�M�͂ǂꂾ�����邩�B �i�q���g�F|G|=8 �ł��� |H|=4�ƂȂ镔���Q��3�A|H|=2�ƂȂ镔���Q��3����B�j ���K���Ƃ��ċ����Ă݂͂����A ��͂�l�@��E��������Ă������Ƃ����ɗ���������Ȃ� [��] �EG = (Z/15Z)* = {1,2,4,7,8,11,13,14} �ł���B ���m�ɂ� G = {��[1],��[2],��[4],��[7],��[8],��[11],��[13],��[14]} �� ��[k] �� �Ă���^k �Ɏʂ��ʑ��ł���B �E�����Q H = {1,2,4,8}(+15Z) �ɑ��� Q(�� = ��+��^2+��^4+��^8) �����߂钆�ԑ̂ł���B �����Q��2���g��̂͂��ł���B ��ʂɏI�������g����"�@�B�I��"�i�����Ă��R���s���[�^���g�������Ȃ�Ƃ����Ӗ��ł��j ��=��+��^2+��^4+��^8�̍ŏ��������邱�Ƃ��ł��� ���������̂悤�ȋ�̓I�Ɏ�v�Z�͈͂ŋ��߂���@������ �� = ��+��^2+��^4+��^8 �� = ��^7+��^11+��^13+��^14 (��]�Q G/H ���l����킯�ł���BG/H = {{1,2,4,8},{7,11,13,14}}) �ȉ��̋c�_�ɂ͕K�v�Ȃ����A���ƃ��͋����̊W�ł���B�Ȃ��Ȃ��ʂɁF ��[k](x) �� x ��8�̋�����^���� ��(X-g(x)) g��G �͗L�����W���������ƂȂ�B x=����K�p���āAG�̌���8���邪���̂���4��g(��)=��, �c���4��g(��)=���ƍ�p����B {(X-��)(X-��)}^4 �͗L�����W���������ł���B �������I�ȍl�@������� (X-��)(X-��)���L�����W���������ł��邱�Ƃ��]���B Q(��)�̌��́A{1,��}�̐��`�����ŕ\����͂��ł���B ������ ��^2�̓W�J���l����B����1�����ŕ\����͂��ł���B ��^2 = �ă�+��^2��+��^4��+��^8�� = ��[1](�ă�) + ��[2](�ă�) + ��[4](�ă�) + ��[8](�ă�) = (��[1]+��[2]+��[4]+��[8]) (�ă�) [�`���I�ɂ��̂悤�ȕ\�L���g���Ă݂�] = (��[1]+��[2]+��[4]+��[8]) (��(��+��^2+��^4+��^8)) = (��[1]+��[2]+��[4]+��[8]) (��^2+��^3+��^5+��^9) = (��^2+��^4+��^8+��) + (��^3+��^6+��^12+��^9) + (��^5+��^10+��^5+��^10) + (��^9+��^3+��^6+��^12) = �� + (-1) + (-2) + (-1) = ��-4 ��B�������ă��� x^2-x+4=0 �̉��ł��邱�Ƃ�������B ���Ȃ킿 Q(��) = Q(��-15) �ł���B �}�`���ւ̉��p http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14145078554 ���̕����Q�ƒ��ԑ� �E�����Q H={1,4,7,13}(+15Z) Q(�� = ��+��^4+��^7+��^13) �����߂钆�ԑ̂� Q(��^10) = Q(��) = Q(��-3) �ł��� �E�����Q H={1,4,11,14}(+15Z) Q(�� = ��+��^4+��^11+��^14) = Q(��^6+��^9) = Q(cos(2��/5)) = Q(��5) �ł���B �E�����Q H={1,14}(+15Z) Q(�� = ��+��^14) = Q(cos(2��)/15) ���̍ŏ��������� x^4-x^3-4x^2+4x+1 �E�����Q H={1,4}(+15Z) Q(�� = ��+��^4) ���̍ŏ��������� x^4-x^3+2x^2+x+1 �E�����Q H={1,11}(+15Z) Q(�� = ��+��^11) = Q(��^6) = 5���̉~���� ���̍ŏ��������� x^4-x^3+x^2-x+1
�E1�̌��n11�捪��p���g��ŕ\��(2015/7/26) 1�̌��n11�捪�����ނɂ��悤�B 5���g����g���̂�1�̌��n5�捪���ĂƂ����Ă����B �� = ��+1/�� �Ƃ����� ����y^5+y^4-4y^3-3y^2+3y+1=0 �����B ���̕������̉�����1,��2,��3,��4,��5 �Ƃ����B �K���A�Q�̌��͔{�p�����ŋ�̓I�ɕ`�ʂ����B���Ȃ킿 Gal(L/K) = {e,f,f^2,f^3,f^4} (e�͍P���ʑ��Af^k��f��k��, f(��) = ��^2-2) ���̂Ƃ� L1 = ��+��f(��)+��^2f^2(��)+��^3f^3(��)+��^4f^4(��) L2 = ��+��^2f(��)+��^4f^2(��)+��^6f^3(��)+��^8f^4(��) L3 = ��+��^3f(��)+��^6f^2(��)+��^9f^3(��)+��^12f^4(��) L4 = ��+��^4f(��)+��^8f^2(��)+��^12f^3(��)+��^16f^4(��) L5 = ��+��^5f(��)+��^10f^2(��)+��^15f^3(��)+��^20f^4(��) �Ƃ����� L1^5, L2^5, L3^5, L4^5, L5^5 �� K �Ɋ܂܂�� �Ƃ����̂����O�����W�F�̃��]���x���g�Ƃ������@�ł���B ������ (L1+L2+L3+L4+L5)/5 = �� �ɂ���ă�����̂ł���B L5=-1 �ł���c��� L1^5,L2^5,L3^5,L4^5 �͎���4���������̉��ƂȂ�B L^4+979L^3+467181L^2+157668929L+25937424601 = 0 ����͍������g�����Ƃʼn�����F L = -979/4 + 275��5/4 �} 55(3+2��5)��((-5-��5)/2), -979/4 - 275��5/4 �} 55(3-2��5)��((-5+��5)/2) ���l�� L = -398.47968�}47.591489*i, -390.85330�}91.020326*i ������"5�捪"�̘a����1��������5�Ŋ��������̂�����^����B L1����L4�̓Ă��g���ĕ\�����Ƃ��ł���F L = 11*(-10��^3+10��^2+25��-16) [���n5�捪��4����̂ł��ꂼ�ꂪL1����L4��^����] L��5�捪�����͐��l�v�Z�� L1�̌��F -1.0996 + 3.1290*i -0.9496 - 3.1778*i -3.3157 - 0.0788*i 2.7288 - 1.8851*i 2.6361 + 2.0127*i L2�̌��F -3.1979 - 0.8795*i -1.8247 + 2.7696*i 3.1041 - 1.1681*i -0.1517 - 3.3132*i 2.0702 + 2.5912*i L3,L4�͂��ꂼ�ꕡ�f���� ������ y^5+y^4-4y^3-3y^2+3y+1 = 0 �̐��l���� -1.918985947228995 -1.30972146789057, -0.28462967654657, 0.83083002600377, 1.682507065662362, (L1+L2+L3+L4-1)/5 �������̒l�ɑΉ������邱�Ƃ��ł����B �Ⴆ�Έ�ԏ�̌��ɂ��āF ((-1.0996+3.1290*i)+(-3.1979-0.8795*i)+(-1.0996-3.1290*i)+(-3.1979+0.8795*i)-1)/5 �� -1.919 # 5�捪�̑g�ݍ��킹�̂��� -1.0996 + 3.1290*i �� -3.1979 - 0.8795*i �� �Ή����� -0.9496 - 3.1778*i ��-1.8247 + 2.7696*i ���Ή����� �E�E�Ƃ����Ή��͂ǂ̂悤�ɒm�邱�Ƃ��ł���̂��F ���ƌW���̊W���� L1^5,L2^5,L3^5,L4^5 �̐ς� 11^10 �ƂȂ��Ă���B 5�捪�̑g�ݍ��킹�� L1*L2*L3*L4 = 121 �����g�ݍ��킹�ƂȂ��Ă��� # �����烿��ɂ� �� = {���}��(��^2-1)}/2 �Ƃ���Ηǂ� ���NjL�F�� = {���}��(��^2-4)}/2 �̊ԈႢ���ƋC�t���� https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13182028133
�E(7+21��-3)/2 ��3�捪��1�̌��n21�捪�ŕ\����(2015/11/23) 1�̌��n21�捪���ĂƂ����� b = (��^10-��^8+��^6+��^5+��^4+��^2-��)�@��3�悪a(�܂��͂��̋���)�ɂȂ� [�w�i�l�@] ��=exp(2��/7) �ɑ��ā@c =��+1/�� = 2cos(2��/7) ���l�@���� c�͎���3�������������F F(x) = x^3+x^2-2x-1 = 0�E�E�@ ���̕������̓J���_�m�̕��@�ʼn�����B c = ({(7+21��-3)/2}^(1/3) + {(7-21��-3)/2}^(1/3) - 1) / 3 ���������킯�� Q(b=a^(1/3))��Q(��+1/��) �Ƃ����b�̍ŏ��������� x^6-7x^3+343 �ł���Q����� (x-b)(x-��b)(x-b/��)(x-b~)(x-��b~)(x-b~/��) �ƕ��������͂� b~��b�̕��f�����ł��� a*(a~) = 7^3 �ł��邱�Ƃ��� b*b~=7 �� b~ = 7/b �ƕ\�����Ƃ��ł��� �܂� �ւ� (b^3-14)/21 �ƕ\�����Ƃ��ł��� ���ǂ��ׂẲ���1�̉��̗L�����ŕ\����Ă���E�E�A ����g�原���̍l�@���� Q(b) �� Q(��+1/��) ��2���g��ł����� �Ƃ���� �ւ� Q(b)�Ɋ܂܂�邪 Q(��+1/��)�ɂ͊܂܂�Ȃ� ���Ȃ킿 Q(b) �� Q(��+1/��,��) �� Q(��+1/��) �����藧�� �g�原���̍l�@���獶��2�͈̑̂�v����͂��ł��� Q(��+1/��,��) �� Q(��,��) = Q(��) ��������B ��ԍ��̒��ԑ̂ɑΉ����� Q(��)/Q �̃K���A�Q�̕����Q�̐������� ���������ɂ��ăւ�ۂ悤�Ȏ��ȏ����^�A���Ȃ킿 ��^3����^(-3), ��^7����^7 �Ƃ���悤�Ȃ��̂ł��� 3k��-3 (mod 21), 7k��7 (mod 21) �����̂� k��13 (mod 21) ���������킯�� Q(��+1/��,��) = Q(��+��^13) �������� ��������̓I��b�̌v�Z�͑������R�ɗ����T��ȊO�Ɍ����Ă��Ȃ� ��T��Ƃ́F 3(��+1/��)+1 = b+7/b ��b�ɂ��ĉ��������ʂ��� ��(-3��^4-2��^3+3��^2-2��-3) �̕�������Q(��)�Ɋ܂܂��͂� resultant((-3x^4-2x^3+3x^2-2x-3)-y^2,��[7](x),x),factor; ���v�Z�@�ɓ�����B�萔����49�ł��邱�Ƃ���m������7�ȓK���Ȍ����g���� resultant((-3x^4-2x^3+3x^2-2x-3)-(1-x)^4*y^2,��[7](x),x),factor; �������Ă݂�ƂȂ�Ƃ��܂���c�̍ŏ����������o������ (��^3+��^4)^2*(1-��)^4 ����L�́�̒��g��^���邱�Ƃ������� �������� b�̋�̓I�ȕ\����������
�@�̕������̌W���� F(x)��(x-2)^3 (mod 7Z[x]) ���g���Ďv���o�����Ƃ��ł��� ���̊W�͎��̂悤�ȁu�ǂ݂����v�ɂ���Đ����ł��� F(x) = (x-��-��^6)(x-��^2-��^5)(x-��^3-��^4) �����藧�B�Ƃ������Ƃ� G(y) = F(x)-(x-y-y^6)(x-y^2-y^5)(x-y^3-y^4) ��y�̕������ƌ��Ȃ��� y=��^k�����ƂȂ��Ă��� �����W���������̈��������͐����W���Ɏ��܂邱�Ƃ����m�Ƃ��� G(y) = (y-��)(y-��^2)...(y-��)^6 * (�����W��������) = (y^6+y^5+y^4+y^3+y^2+y+1) * (�����W��������) �̊W��By=1 ��������� G(1)��0 (mod 7Z[x]) ���Ȃ킿 F(x)��(x-2)^3 (mod 7Z[x]) �A����Q(b)/Q �̓K���A�g��ł��肻�̃K���A�Q�̓A�[�x���Q�� �N���l�b�J�[�E�F�[�o�[�̒藝�ɂ�肠��~���̂Ɋ܂܂��͂� �Ƃ������Ƃ�������
[2015/3/29�NjL] http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13157511943 (14-��-7+3��21)/2 ��3�捪��1�̌��n21�捪�ŕ\����͂��ł��� ���ł́@��̓I��b�̌v�Z�͑������R�ɗ����T��������������m���ȕ��@��g�ɂ��Ă���̂ŏЉ�� 1�̌��n21�捪��a�Ƃ����BA^3 = 2*a^11+4*a^9+2*a^8-3*a^7-4*a^4+6*a^2-4*a+6 ��3�捪��m�肽�� 1�̌��n21�捪a�ɂ��g���Q(a)���l�@����B�������������Ƃ��̐����ł���Z(a)�ōl�@���� http://www.lmfdb.org/NumberField/ �ŊY���̃y�[�W�ɒH������@�͂��������邪�A�Ⴆ�K���A�Q��C6xC2�Ǝw�肷��Əo��� http://www.lmfdb.org/NumberField/12.0.205924456521.1 �ސ����K���ɂP�ł��邱�ƁA�P���Q���T�̌��Ő�������邱�ƁA���̐������@�̏���p�ł��� A^3 �̃m������7^9�ł��邱�Ƃ���A�܂���(7)��f�C�f�A���������� �m������7�ƂȂ錳��T���B�n���I�ȒT�����͂܂��m��Ȃ������ꂮ�炢�Ȃ�K���ɒT���ĂȂ�Ƃ���������i�����ő������R�ɗ���j http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14156999604 (1+a^4-a^5+a^6)�@���@�m������7�̌��Ƃ��ē���ꂽ (7) = (1+a^4-a^5+a^6)^6 * (1+a^17-a^16+a^15)^6[�C�f�A���Ƃ��ē������Ƃ����Ӗ�] A^3 = (1+a^4-a^5+a^6)^6 * (1+a^17-a^16+a^15)^3 * (�P��)�@����B (�P��)�̕������v�Z����� 33601*a^11-26238*a^10-28798*a^9+12256*a^8-32712*a^7-18156*a^6+36312*a^5+30001*a^4-20338*a^3 +18156*a^2+2182*a-48157 �P���� ��L��URL�� Torsion generator, Fundamental units �Ő�������� ��̓I�ɂ� (a^3+1),(a^10-a^8+a^3),(a-1),(a^2-1),(a^4-1) �� a1,a2,a3,a4,a5 �Ɩ��t���Ă����� �C�ӂ̒P���� �����̐����p��a�̙p���|�����킹�ē�����͂��ł���B �^����ꂽ�P���ɑ��� Fundamental units �̐ςł̕\�� �����߂�ɂ́A�������Љ���y�[�W�ł̎��̕ԐM�ɏ����Ă�����@���g���� http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14156999604 �㐔��L�̏�@�Q�@����@R�̉��@�Q�@�ւ̖��ߍ��݂�6��ނ��� �iL����L�ւ̎��ȓ��^��12��ނ����āA���ꂼ����o�R���Ă��畡�f��Βl���Ƃ�� 12��ނ̂���2��ނ��͕��f�����̊W������A6��ނ̎����ߍ��݂����݂���킯�ł���j ����Ł@A^3 = (1+a^4-a^5+a^6)^6 * (1+a^17-a^16+a^15)^3 * a1^3* a2^9 * a3^(-3) * a4^3 * a5^6 * a^15 ��������B�������� 3�悵�� A^3 �ɂȂ���̂����߂邱�Ƃ��ł���i���̂�����1��a^7,a^14���|�������̂��c���2�ł���j
2016/7/6 �NjL 1�̌��n21�捪�̐�������̂ƒ��ԑ̂ƃK���A�Q�̕����Q�̍l�@���q�ׂĂ݂�B �~���̂́A���̃K���A�Q�����ł��邱�Ƃ��A�l�@�ɗL���ł���B [���i�K�F�K���A�Q] ��=exp(2��i/21)�̍ŏ���������x^21-1�̈�����1�ł�����ۂɂ� ��(x) = x^12-x^11+x^9-x^8+x^6-x^4+x^3-x+1 �ł���B�i�~���������j Q(��)/Q ��12���g��ł���A Q(��)�̌��̓Ă�11���ȉ���Q�W���������ň�ӓI�ɕ\����� �����ŁA21�ƌ݂��ɑf�Ȑ���k�ɑ��āA �Ă���^k�ɒu��������Ƃ����ʑ���[k]���l����B ���̂���₷�����邽�߂ɗ��������Ƃ����� ��[2](1+��^4+��^5) = 1+��^8+��^10 ��[8](��^10+2��^11) = ��^80+2��^88 = ��^17+2��^4 �̂悤�ȍ�p������Q(��)����Q(��)�ւ̎ʑ��ł���B ���ꂪQ���Œ肷�鎩�ȓ��^�ʑ���^���Ă���B ����k��20 (mod 21) �̂Ƃ��͕��f�����ʑ��ł���B ���Ȃ킿�K���A�Q Gal(Q(��)/Q)�͏W���Ƃ��Ă� {��[k]|k��21�ƌ݂��ɑf} �ŕ\�����8��ނ̌������W���ł��� �Q�̉��Z�Ƃ��Ă� ��[j]�ƃ�[k]�̉��Z�́A�ʑ��Ƃ��Ă̍����A���Ȃ킿��[jk]�ŗ^������B �ij��k��21�ƌ݂��ɑf�Ȃ��jk��21�ƌ݂��ɑf�����牉�Z�͕��Ă���j ���̂悤�ɂ��� Gal(Q(��)/Q)�͎��R�� �u�����]�ނ��Ȃ���@�Q�v�ɓ��ꎋ�ł���B �ȗ�������G={1,2,4,5,8,10,11,13,16,17,19,20}�Ə����B �i���Z�́A21��@�Ƃ���ςŗ^������B�j ---------- [���i�K�F�����Q] G�̕����Q�����ׂċ�����Ƃ����ۑ�͏����ɌQ�̖��ł���B �����Q�Ƃ́A���Z�����Ă���悤��G�̕����W���̂��Ƃł���B ��̉摜�Ɏ������悤�ɁA���g���܂߂�9�̕����Q�����݂���B ��������ʂ��悭���������ɂ́A �u�����]�ނ��Ȃ���@�Q�v�̍\����m���Ă���Ɨǂ��B ���Ȃ킿3�Ŋ������]���7�Ŋ������]��̑g�ɕ������邱�Ƃ� (Z/21Z)�̏�@�Q�́A(Z/3Z�̏�@�Q)��(Z/7Z�̏�@�Q)�̒��ςƂ݂Ȃ� ���ꂼ��ɂ��Ă�p���f���̎�Z/pZ�̏�@�Q��(p-1)�̌�����Ȃ鏄��Q�ł���B ���o�I�ɂ͉�������6�}�X�Ń��[�v�A�c������2�}�X�Ń��[�v����}�X�ڂƂ��� 1 , 10 , 16 , 13 , 4 , 19 8 , 17 , 2 , 20 , 11 , 5 �ƕ��ׂĂ݂Č�̉摜�̕����Q���ǂ̂悤�ȕ��z�����Ă���̂������邱�ƂŎ��̈Ӑ}���`���Ɨǂ� �i�����0�s0��Ƃ��Đ��������Aa�sb���c�sd��̉��Z���ʂ�a+c�sb+d��ɂȂ��Ă���Ƃ����Ӑ}�ł���j
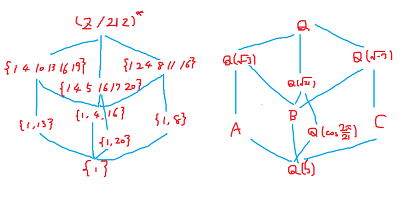 [��O�i�K�F���ԑ�]
�����Q�ɑΉ����钆�ԑ̂́A�u�Œ�́v�œ����Â�����B
�Ⴆ��{1,4,16}�Ƃ��������Q�A���m�ɂ�{��[1],��[4],��[16]}�Ƃ��������Q�ɑΉ����钆�ԑ̂́A
B = {x��Q(��) | ��[1](x)=x ���� ��[4](x)=x ���� ��[16](x)=x}
�Ƃ���Q(��)�̕����W���ł���B
�i��[1]�͍P���ʑ��ł��邵��[16]�̓�[4]��2���p���������̂�����
�����Ƃ��Ă� B={x��Q(��)|��[4](x)=x}�Ə����Ă������ł���j
�K���A���_���咣���邱�Ƃɂ́A
�E�����Q�ƒ��ԑ̂�1��1�ɑΉ�����
�E�����QH�ɑΉ����钆�ԑ̂�M�Ƃ�����
�����QH�� Q(��)/M �̃K���A�Q�Ƃ݂Ȃ����Ƃ��ł���B
�܂�H��G�̐��K�����Q�ł���Ȃ�i���Q�ł͏�ɖ��������j
��]�QG/H �� M/Q �̃K���A�Q�Ƃ݂Ȃ����Ƃ��ł���
���ԑ̂ɑ����錳�̋�̗�Ƃ��Ď��͏d�v�ł���B
Gal(Q(��)/Q) �̕����Q {��[k]|k��H} ���l����B
����^k [k��H] �͂��̕����Q�ɑΉ����钆�ԑ̂ɑ�����B
�i�C���[�W�̂��߂ɂ͗Ⴆ�Ώ�L��B�Ƃ������ԑ̗̂�Ƃ���
��+��^4+��^16 �Ƀ�[4]����p�����ĕs�ςł��邱�Ƃ��m���߂�j
�i�]�T�������Q(��)/B��B/Q�̃K���A�Q���l�@���Ă݂�j
�����̓���ɂ����
�Ă̑������ŕ\����镡�f�������^����ꂽ�Ƃ��A
��[k]��������Œ肷��悤��k�ׂ邱�Ƃ�
�u�����ǂ̒��ԑ̂ɑ����A�ǂ̒��ԑ̂ɑ����Ȃ����v
��m�邱�Ƃ��ł���̂ł���B
�܂��g�原���̏��A���ԑ�M�ɑ���
����M�W���ł̍ŏ��������̎�����m�邱�Ƃ��ł���B
�Ⴆ�Ύ��̂悤�ȋc�_���\�ƂȂ�F
�E��=��+��^13���Œ肷��悤�ȃ�[k]��k=1,13�݂̂�����
���͉摜��A�Ƃ������ԑ̂ɑ����A�����菬���Ȓ��ԑ̂ɂ͑����Ȃ��B
�]����A=Q(��)�ł���B
���̍ŏ���������6�����ł���AA�̔C�ӂ̌��̓���5���ȉ��̑������Ƃ��Ĉ�ӓI�ɕ\����B
���ۃ�+��^13�̍ŏ���������X^6-X^5+3X^4+5X^2-2X+1 �Ƃ���Q������6�����ł���
�E��+��^20=2cos(2��/21)�ɂ��Ă����l�ł���B
��[20]�͕��f�����ʑ��ł��邩��A
���̒��ԑ� Q(cos(2��/21))�� Q(��)�̂����������Ȃ����ԑ̂Ƃ�������B
�E�����Q{1,4,10,13,16,19}�ɑ����錳�Ƃ���
��+��^4+��^10+��^13+��^16+��^19 �����݂���B
�Ƃ��낪�����-��^7�̂��Ƃł���A(1-��-3)/2�̂��Ƃł���B
�Ή����钆�ԑ̂͂�����܂ނ悤��Q��2���g��̂ł��邩��Q(��-3)�ł���
�i�ÂɎ��̂悤�ȑ̘_�I������g���Ă���F
L��M��K�ƂȂ��L,M,K��������
L/K��M/K�̊g�原�����i���ɗL���Łj�������Ȃ��L=M�ł���j
�E��+��^2+��^4+��^8+��^11+��^16 = -(��^9+��^15+��^18) �ł���B
1�̌��n7�捪��z�Ƃ����{z+z^2+z^4,z^3+z^5+z^6}=(-1�}��-7)/2�ł��邱�ƂɋA������B
�Ή����钆�ԑ̂�Q(��-7)�ł���
�E�����P�̌���6�Ȓ��ԑ̂ɑΉ����钆�ԑ͕̂K�R�I��Q(��21)�ł���
�E�������܂�4���g���B�͕K�R�I��Q[��-3,��-7,��21]�ł���B
�]����B�ɑ�����悤�ȕ��f��
y=��+��^4+��^16 (�����y^4-y^3-y^2-2y+4=0 �̉�)
��1,��-3,��-7,��21�̐��`�����ŕ\����͂��ł���B
�E�g�原������cos(2��/21)��Q(��21)�W���ŏ���������3���ł��邱�Ƃ�������B
[��O�i�K�F���ԑ�]
�����Q�ɑΉ����钆�ԑ̂́A�u�Œ�́v�œ����Â�����B
�Ⴆ��{1,4,16}�Ƃ��������Q�A���m�ɂ�{��[1],��[4],��[16]}�Ƃ��������Q�ɑΉ����钆�ԑ̂́A
B = {x��Q(��) | ��[1](x)=x ���� ��[4](x)=x ���� ��[16](x)=x}
�Ƃ���Q(��)�̕����W���ł���B
�i��[1]�͍P���ʑ��ł��邵��[16]�̓�[4]��2���p���������̂�����
�����Ƃ��Ă� B={x��Q(��)|��[4](x)=x}�Ə����Ă������ł���j
�K���A���_���咣���邱�Ƃɂ́A
�E�����Q�ƒ��ԑ̂�1��1�ɑΉ�����
�E�����QH�ɑΉ����钆�ԑ̂�M�Ƃ�����
�����QH�� Q(��)/M �̃K���A�Q�Ƃ݂Ȃ����Ƃ��ł���B
�܂�H��G�̐��K�����Q�ł���Ȃ�i���Q�ł͏�ɖ��������j
��]�QG/H �� M/Q �̃K���A�Q�Ƃ݂Ȃ����Ƃ��ł���
���ԑ̂ɑ����錳�̋�̗�Ƃ��Ď��͏d�v�ł���B
Gal(Q(��)/Q) �̕����Q {��[k]|k��H} ���l����B
����^k [k��H] �͂��̕����Q�ɑΉ����钆�ԑ̂ɑ�����B
�i�C���[�W�̂��߂ɂ͗Ⴆ�Ώ�L��B�Ƃ������ԑ̗̂�Ƃ���
��+��^4+��^16 �Ƀ�[4]����p�����ĕs�ςł��邱�Ƃ��m���߂�j
�i�]�T�������Q(��)/B��B/Q�̃K���A�Q���l�@���Ă݂�j
�����̓���ɂ����
�Ă̑������ŕ\����镡�f�������^����ꂽ�Ƃ��A
��[k]��������Œ肷��悤��k�ׂ邱�Ƃ�
�u�����ǂ̒��ԑ̂ɑ����A�ǂ̒��ԑ̂ɑ����Ȃ����v
��m�邱�Ƃ��ł���̂ł���B
�܂��g�原���̏��A���ԑ�M�ɑ���
����M�W���ł̍ŏ��������̎�����m�邱�Ƃ��ł���B
�Ⴆ�Ύ��̂悤�ȋc�_���\�ƂȂ�F
�E��=��+��^13���Œ肷��悤�ȃ�[k]��k=1,13�݂̂�����
���͉摜��A�Ƃ������ԑ̂ɑ����A�����菬���Ȓ��ԑ̂ɂ͑����Ȃ��B
�]����A=Q(��)�ł���B
���̍ŏ���������6�����ł���AA�̔C�ӂ̌��̓���5���ȉ��̑������Ƃ��Ĉ�ӓI�ɕ\����B
���ۃ�+��^13�̍ŏ���������X^6-X^5+3X^4+5X^2-2X+1 �Ƃ���Q������6�����ł���
�E��+��^20=2cos(2��/21)�ɂ��Ă����l�ł���B
��[20]�͕��f�����ʑ��ł��邩��A
���̒��ԑ� Q(cos(2��/21))�� Q(��)�̂����������Ȃ����ԑ̂Ƃ�������B
�E�����Q{1,4,10,13,16,19}�ɑ����錳�Ƃ���
��+��^4+��^10+��^13+��^16+��^19 �����݂���B
�Ƃ��낪�����-��^7�̂��Ƃł���A(1-��-3)/2�̂��Ƃł���B
�Ή����钆�ԑ̂͂�����܂ނ悤��Q��2���g��̂ł��邩��Q(��-3)�ł���
�i�ÂɎ��̂悤�ȑ̘_�I������g���Ă���F
L��M��K�ƂȂ��L,M,K��������
L/K��M/K�̊g�原�����i���ɗL���Łj�������Ȃ��L=M�ł���j
�E��+��^2+��^4+��^8+��^11+��^16 = -(��^9+��^15+��^18) �ł���B
1�̌��n7�捪��z�Ƃ����{z+z^2+z^4,z^3+z^5+z^6}=(-1�}��-7)/2�ł��邱�ƂɋA������B
�Ή����钆�ԑ̂�Q(��-7)�ł���
�E�����P�̌���6�Ȓ��ԑ̂ɑΉ����钆�ԑ͕̂K�R�I��Q(��21)�ł���
�E�������܂�4���g���B�͕K�R�I��Q[��-3,��-7,��21]�ł���B
�]����B�ɑ�����悤�ȕ��f��
y=��+��^4+��^16 (�����y^4-y^3-y^2-2y+4=0 �̉�)
��1,��-3,��-7,��21�̐��`�����ŕ\����͂��ł���B
�E�g�原������cos(2��/21)��Q(��21)�W���ŏ���������3���ł��邱�Ƃ�������B
�E����1�̙p���ŕ\����鎞�ɂ������������ http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13136172733 http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14152494279 3���������̏ꍇ�͎��̂悤�ɂ��ĉ\���ǂ�����ł��� ����1�̙p���ŕ\�����@�́@���ʎ��������� http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13153067293 ����1�����čl�@���@���Љ�悤�F�@F = y^4-3y^3+19y^2+33y+71 = 0 �܂�1�̉��捪���g���Ηǂ�����������B����ɂ͔��ʎ����L�p�ł���BD(F) = 5^3*11^2*181^2 ���ɑf�����W�����ώ@����̂��L�p�ƂȂ� F(-1)=-61, F(1)=11^2, F(2)=5*41, F(3)=11*31 �ȂǁE�E 5��5N+1�^�f���݂̂������X���������� Q(z)�Ńm������71�ɂȂ�悤�Ȍ���K���Ɍ����� ������z=exp(2��i/5), H=z^4+z^3+z^2+z+1�̍� N(z+k) ��K���Ɏ����� N(z-5) = 11*71 N(z+2)=11 �ł��邱�Ƃ��� (z-5)/(z^k+2) �̌`�ő㐔�I�����ɂȂ���̂�T�� (z-5)/(z^4+2) ���Y������ y = (z-5)/(z^4+2)*x �Ƃ�����x�̍ŏ������������߂� resultant(resultant(H,y/((z-5)/(z^4+2))-x,z),F(y),y) �̈����̂P���� G(x) = x^4+x^3+6*x^2-4*x+1 = 0 �ȏ�ɂ��܂��͒萔����1�̏ꍇ�ɋA���ł��� ���Ɏ��ȏꍇ�ɋA��������B resultant(resultant(H,x/z-u,z),G(x),x) �̈�����1����@f(u) = u^2+3u+1 �� ���P���� �}(sina��)/(sinb��)�̂������̐ςŕ\����B��=2��/5 resultant(resultant(H,u*(z^2-1/z^2)/(z-1/z))-v,z),f(u),u) �ŌW�������������Ă����悤�ɂ������܂鏊�ɂ����� ���Ƃ͍ŏ������������̂nj��Z���ċ����������� u = -(sin2��)^2/(sin��)^2 = -z^3-z^2-2 x = u*z^2 y = (z^3-5)/(z^12+2)*x ���������E����̗L�����ɂ��W���`�ɒ����� y = -z^3+3*z^2-z+1 �� �����������߂�@y = -z^3+3*z^2-z+1, -3z^3-4z^2-4z-2, z^2+4z+2, 4z^3+z+2
���̌�A�����Ƌ@�B�I�ȕ��@�ɏo������B ����ʓI�� G(x)=0 �̉��̂P�����Ƃ��� F(x)��Q(��)�W���ŕ���������@�ɏo������B ������͌������u���^��722 ��1990 �N17-20 �@���g���j ���@(�d�q�Z�p����������) �@�@����Q���K���A�Q�Ɏ���5 ���������̔��ʂƂ��̉�@ http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0722-02.pdf �ȉ��Ȃǂŋ�̓I��maxima�R�}���h�ƂƂ��ɏЉ�Ă���B http://www004.upp.so-net.ne.jp/s_honma/mathbun/mathbun606.html https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11157391336
�E4���������̘b�� �ushanks�̍P�����v ��(22+2��(5))+��(5)=��(11+2��(29))+��(16-2��(29)+2��(55-10��(29))) �̎��� http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12155944522 f(y)=y^4-54*y^2-40*y+269=0 �̍ŏ�����̂��ނ� �K���A�Q�̕����Q�ƒ��ԑׂ̂�ߒ����Љ�Ă݂悤 f(y)=0��4�̉��͎��̂悤�ɕ\���ł���F a = ��5+��(22+2��5) b =-��5+��(22-2��5) c = ��5-��(22+2��5) d =-��5-��(22-2��5) �ŏ������ L = Q(a,b,c,d) ���l����ia,b,c,d�̗L�����ŏ����鐔�̏W���Ƃ����Ӗ��ł���j L/Q �̃K���A�Q��D4���Ƃ����O�����B �Ƃ������Ƃ�L�̌���Q����`�Ɨ��Ȍ���8�Ƃ��͂��ł���B --- a^2 = 27+2��5 + 2��(110+10��5) a^3 = 30+71��5 + 37��(22+2��5) + 2��(110+10��5) ��(22+2��5)*��(22-2��5) = 4��29 �Ȃǂ���A���̂悤��"���`���"���Ƃ邱�Ƃɂ���F {1,��5,��29,��145,��(22+2��5),��(110+10��5),��(22-2��5),��(110-10��5)} ���̏��� {1,X,Y,XY,Z,XZ,W,XW} �Ƃł����t���邱�Ƃɂ����B �����͐��`�Ɨ��ł���L�̔C�ӂ̌��͂����̐��`�����ŕ\�����B --- L/Q �̃K���A�QG �̌�g�Ƃ�Q�̌����Œ肷��L����L�ւ̎��ȓ��^�ʑ��ł���B �܂�L�̌� x,y�ɑ���g(x)g(y)=g(xy),g(x+y)=g(x)+g(y)���� ������Ƃ����l�@�ŁAg(Z),g(W)�����߂�� �ʑ�g�͌��肳��邱�Ƃ�������B �Ȃ��Ȃ� g(Y)=g(ZW/4), g(X)=g((Z^2-22)/2) �����藧����ł���B g(Z)����蓾�����4�ł���BZ,-Z,W,-W�̂ǂꂩ�ł���B �Ȃ��Ȃ� (Z^2-22)^2 - 20 = 0 �����藧���Ƃ� ���ȓ��^������ (g(Z)^2-22)^2 - 20 �����藧�K�v�����邩��ł���Bg(W)�����l�ł���B g(Z)=�}Z,g(W)=�}W �ƂȂ�ꍇ�� g(Z)=�}W,g(W)=�}Z �ƂȂ�ꍇ��4�ʂ肸�� ���̂悤�ɂ��Ċm���� G�̌���8����B [��] g(Z)=W,g(W)=W �̂悤�ȏꍇ���s�K�ł��邱�Ƃ�[������B --- D4�Ƃ͈ʐ�8�̓�ʑ̌Q�Ƃ������̂ł��邪�A ����͐����`�����g�ɍ����ɏd�˂�悤�ȕϊ��̌Q�Ƃ����R���ł���B ���ہA�����`�̒��_�� Z,W,-Z,-W �Ɩ��t����A��L�ƑΉ�����B �i�����`�̍����ϊ��͐�ɏq�ׂ��悤�ȕϊ��������N���� �t�ɐ�ɏq�ׂ��悤�ȕϊ��͐����`�̍����ϊ��������N�����j
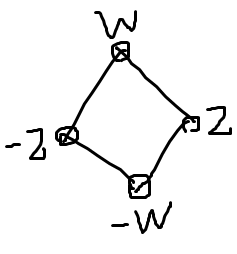 ���̌Q�͎��̂Q�̌��Ő��������B
����90�x�܂킷��s�ƁA�㉺�]������t�ł���B��p�Ƃ��Ă�
s([Z,W]) = [W,-Z] �� t([Z,W])=[Z,-W] �ł���B
st �̂悤�ɏ������Ƃ��A����� t,s�̏��ɍ�p�����錳���Ӗ����邱�ƂƂ���B
���Ȃ킿 (st)([Z,W]) = s(t([Z,W])) = s([Z,-W]) = [W,Z]
st��ts �ł��邱�Ƃɒ��ӂ���B
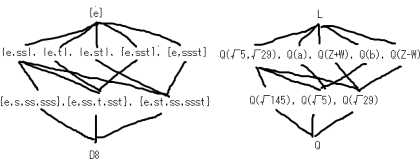
D4 = {e,s,ss,sss,t,st,sst,ssst} �ł���B(e�͒P�ʌ�)
[��] ts�͂��̂����ǂꂩ�Ɠ������B�ǂꂩ�B
D4�̕����Q�Ƃ́AD4�̕����W���ʼn��Z�ɂ��ĕ��Ă�����̂ł���B
�����Q������Ȃ������o���͈̂ӊO�Ɠ���B
����2����Ȃ镔���Q��5����B
{e,ss}, {e,t}, {e,st}, {e,sst}, {e,ssst}
����4����Ȃ镔���Q��3����B
{e,s,ss,sss},{e,ss,t,sst}, {e,st,ss,ssst}
�i���Ɏ����ȕ����Q{e} �� D8���̂�����B�j
����畔���Q�ƁAQ��M��L �ƂȂ钆�ԑ�M��1��1�ɑΉ�����Ƃ����̂��K���A�̊�{�藝�ł���B
G�̕����QH�ɑ��钆�ԑ�M�́A{H�̂ǂ̌��ɑ��Ă��s�ς�L�̌�}���Ή�����B
�����ȕ����Q�ɂ�L���Ή����AD4���̂ɂ́AQ���Ή�����B
����2����Ȃ镔���Q�ɂ́AQ��4���g��ƂȂ钆�ԑ̂��A
����4����Ȃ镔���Q�ɂ́AQ��2���g��ƂȂ钆�ԑ̂��Ή�����B
L�̐��`���ւ�G�̌��̍�p�����߂邱�Ƃɂ��A�s�ϑ̂�������₷���B
s([1,X,Y,XY,Z,XZ,W,XW]) = [1,-X,-Y,XY,W,-XW,-Z,XZ]
t([1,X,Y,XY,Z,XZ,W,XW]) = [1,X,-Y,-XY,Z,XZ,-W,-XW]
st([1,X,Y,XY,Z,XZ,W,XW]) = [1,-X,Y,-XY,W,-XW,Z,-XZ]
ss([1,X,Y,XY,Z,XZ,W,XW]) = [1,X,Y,XY,-Z,-XZ,-W,-XW]
ssst([1,X,Y,XY,Z,XZ,W,XW]) = [1,-X,Y,-XY,-W,XW,-Z,ZW]
sst([1,X,Y,XY,Z,XZ,W,XW]) = [1,X,-Y,-XY,-Z,-XZ,W,XW]
{e,s,ss,sss} �ŕs�ρF[1,XY] ���Ȃ킿 Q(��145)
{e,ss,t,sst} �ŕs�ρF[1,X] ���Ȃ킿 Q(��5)
{e,st,ss,ssst} �ŕs�ρF[1,Y] ���Ȃ킿 Q(��29)
{e,ss} �ŕs�ρF[1,X,Y,XY] ���Ȃ킿 Q(��5,��29)
{e,t} �ŕs�ρF[1,X,Z,XZ] ����� Q(a)�ƈ�v����(��)
{e,sst}�ŕs�ρF[1,X,W,XW] ����� Q(b)�ƈ�v����B
{e,st}�ŕs�ρF[1,Y,Z+W,XW-XZ] �� Q(Z+W)�Ə�����B(��2)
{e,ssst}�ŕs�ρF[1,Y,Z-W,XZ+XW] �� Q(Z-W)�Ə�����B
(��) a=X+Z, a^2=27+2X + 2XZ, a^3=30+71X+37Z+2XZ ���
a�̑�������{1,X,Z,XZ}�̐��`�����ŕ\�����Ƃ��ł��Ă���B
�t�� {X,Z,XZ} ��ϐ��Ƃ���A���������ƌ��Ȃ��ĉ�����
X,Z,XZ �� a�̑������ŕ\����B
�Ȃ����̂��Ƃ��� c=X-Z ��a�̑������ŕ\���邱�Ƃ�������B
(��2) (Z+W)^2 = 44+8Y, (Z+W)^3 = 44(Z+W)+8Y(Z+W) = 88(Z+W)+4(XW-XZ)
��4YZ=ZWZ=(22+2��5)W=22W+2XW, ���l�� 4YW=22Z-2XZ
�����肷����̋c�_��a�̖�����(Z+W)�ɂ����ē��l�̋c�_�B
�������܂Ƃ߂āA�K���A�Q�̕����Q��L/Q�̒��ԑ̂̑Ή��}����������B
���̌Q�͎��̂Q�̌��Ő��������B
����90�x�܂킷��s�ƁA�㉺�]������t�ł���B��p�Ƃ��Ă�
s([Z,W]) = [W,-Z] �� t([Z,W])=[Z,-W] �ł���B
st �̂悤�ɏ������Ƃ��A����� t,s�̏��ɍ�p�����錳���Ӗ����邱�ƂƂ���B
���Ȃ킿 (st)([Z,W]) = s(t([Z,W])) = s([Z,-W]) = [W,Z]
st��ts �ł��邱�Ƃɒ��ӂ���B
D4 = {e,s,ss,sss,t,st,sst,ssst} �ł���B(e�͒P�ʌ�)
[��] ts�͂��̂����ǂꂩ�Ɠ������B�ǂꂩ�B
D4�̕����Q�Ƃ́AD4�̕����W���ʼn��Z�ɂ��ĕ��Ă�����̂ł���B
�����Q������Ȃ������o���͈̂ӊO�Ɠ���B
����2����Ȃ镔���Q��5����B
{e,ss}, {e,t}, {e,st}, {e,sst}, {e,ssst}
����4����Ȃ镔���Q��3����B
{e,s,ss,sss},{e,ss,t,sst}, {e,st,ss,ssst}
�i���Ɏ����ȕ����Q{e} �� D8���̂�����B�j
����畔���Q�ƁAQ��M��L �ƂȂ钆�ԑ�M��1��1�ɑΉ�����Ƃ����̂��K���A�̊�{�藝�ł���B
G�̕����QH�ɑ��钆�ԑ�M�́A{H�̂ǂ̌��ɑ��Ă��s�ς�L�̌�}���Ή�����B
�����ȕ����Q�ɂ�L���Ή����AD4���̂ɂ́AQ���Ή�����B
����2����Ȃ镔���Q�ɂ́AQ��4���g��ƂȂ钆�ԑ̂��A
����4����Ȃ镔���Q�ɂ́AQ��2���g��ƂȂ钆�ԑ̂��Ή�����B
L�̐��`���ւ�G�̌��̍�p�����߂邱�Ƃɂ��A�s�ϑ̂�������₷���B
s([1,X,Y,XY,Z,XZ,W,XW]) = [1,-X,-Y,XY,W,-XW,-Z,XZ]
t([1,X,Y,XY,Z,XZ,W,XW]) = [1,X,-Y,-XY,Z,XZ,-W,-XW]
st([1,X,Y,XY,Z,XZ,W,XW]) = [1,-X,Y,-XY,W,-XW,Z,-XZ]
ss([1,X,Y,XY,Z,XZ,W,XW]) = [1,X,Y,XY,-Z,-XZ,-W,-XW]
ssst([1,X,Y,XY,Z,XZ,W,XW]) = [1,-X,Y,-XY,-W,XW,-Z,ZW]
sst([1,X,Y,XY,Z,XZ,W,XW]) = [1,X,-Y,-XY,-Z,-XZ,W,XW]
{e,s,ss,sss} �ŕs�ρF[1,XY] ���Ȃ킿 Q(��145)
{e,ss,t,sst} �ŕs�ρF[1,X] ���Ȃ킿 Q(��5)
{e,st,ss,ssst} �ŕs�ρF[1,Y] ���Ȃ킿 Q(��29)
{e,ss} �ŕs�ρF[1,X,Y,XY] ���Ȃ킿 Q(��5,��29)
{e,t} �ŕs�ρF[1,X,Z,XZ] ����� Q(a)�ƈ�v����(��)
{e,sst}�ŕs�ρF[1,X,W,XW] ����� Q(b)�ƈ�v����B
{e,st}�ŕs�ρF[1,Y,Z+W,XW-XZ] �� Q(Z+W)�Ə�����B(��2)
{e,ssst}�ŕs�ρF[1,Y,Z-W,XZ+XW] �� Q(Z-W)�Ə�����B
(��) a=X+Z, a^2=27+2X + 2XZ, a^3=30+71X+37Z+2XZ ���
a�̑�������{1,X,Z,XZ}�̐��`�����ŕ\�����Ƃ��ł��Ă���B
�t�� {X,Z,XZ} ��ϐ��Ƃ���A���������ƌ��Ȃ��ĉ�����
X,Z,XZ �� a�̑������ŕ\����B
�Ȃ����̂��Ƃ��� c=X-Z ��a�̑������ŕ\���邱�Ƃ�������B
(��2) (Z+W)^2 = 44+8Y, (Z+W)^3 = 44(Z+W)+8Y(Z+W) = 88(Z+W)+4(XW-XZ)
��4YZ=ZWZ=(22+2��5)W=22W+2XW, ���l�� 4YW=22Z-2XZ
�����肷����̋c�_��a�̖�����(Z+W)�ɂ����ē��l�̋c�_�B
�������܂Ƃ߂āA�K���A�Q�̕����Q��L/Q�̒��ԑ̂̑Ή��}����������B
 �Eb��a��Q(��29)�W���������ŏ����邱��
{1,X,Z,XZ} �̐��`������A�̑������ŏ����邱�Ƃ��������Ă���B
4YZ = 22W+2XW, 4YXZ = 22XW+10W ���t�ɉ����� W�� 4YZ, 4YXZ �̐��`�����ŏ�����B
�E���l��b��a��Q(��145)�W���������ŏ����邱�Ƃ�������B
�Eb��a��Q(��29)�W���������ŏ����邱��
{1,X,Z,XZ} �̐��`������A�̑������ŏ����邱�Ƃ��������Ă���B
4YZ = 22W+2XW, 4YXZ = 22XW+10W ���t�ɉ����� W�� 4YZ, 4YXZ �̐��`�����ŏ�����B
�E���l��b��a��Q(��145)�W���������ŏ����邱�Ƃ�������B
�E4����������4�̉���a,b,c,d�Ƃ���B�K���A�Q��S4�ɂȂ�ꍇ�� [Q(a,b,c,d):Q]=24, [Q(a,b):Q] = 12, [Q(a):Q] = 4 �̊W�ł��� ���̎��_�Ŏ��̂悤�ȍl�@���ł����F http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14156018199 �K���A�Q��A4�ɂȂ�ꍇ�� [Q(a,b,c,d):Q]=12, [Q(a):Q] = 4 �ł���BQ(a,b,c,d)=Q(a,b)�ł���B ���̂��Ƃ���c,d��a,b�̗L�����ŏ�����͂��ł���B �Ⴆ�� F(x) = x^4-2x^3+2x^2+2 = 0 �̉�a,b,c,d�ɂ��čl�����B http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q10156016795 �E�B�L�y�f�B�A�ɏЉ��Ă���u�I�C���[�̕��@�v���� a-1/2=-x-y-z, b-1/2=-x+y+z, c-1/2=x-y+z, d-1/2=x+y-z, A=4x^2, B=4y^2, C=4z^2, A,B,C �� f(u)=u^3+u^2-9*u-1=0 �̉� �Ƃ����� A,B,C�̊Ԃɑ������W������ B=(A^2-7)/2, C=(B^2-7)/2 ���̊W�̋@�B�I�ȋ��ߕ��� http://www004.upp.so-net.ne.jp/s_honma/solution/solution3.htm �ŏЉ��Ă���B �����̊W���� A = (a+b-1)^2 B = ((a+b-1)^4-7)/2 C = ((((a+b-1)^4-7)/2)^2-7)/2 B-C = 4y^2-4z^2 = (a-b)(c-d) ��� c-d = (B-C)/(a-b) ��� c+d-1 = 2x = -(a+b-1) c = (-a-b+2+(B-C)/(a-b))/2, d = (-a-b+2-(B-C)/(a-b))/2 �ɂ���� c,d��a,b�̗L�����ŕ\�����Ƃɐ�������B Q(a,b)�̌���a��3���ȉ�, b��2���ȉ��̑������ň�ӓI�ɕ\����B���̌`�ɂ���ƁF c = -((a^3-3*a^2-2*a+2)*b^2+(-4*a^3+12*a^2-6*a+6)*b+2*a^3-6*a^2+10*a-10)/14 d = ((a^3-3*a^2-2*a+2)*b^2+(-4*a^3+12*a^2-6*a-8)*b+2*a^3-6*a^2-4*a+18)/14 �邱�Ƃɐ�������B �i�]�k�F���Ȃ݂ɂ��̕��������f(u)�̓K���A�Q��Z/3Z�ł���A�[�x���Q�ł��� ���̂悤�ȂƂ�f(u)�̌���1�̌��nn�捪�ŕ\����̂��N���l�b�J�[�E�F�[�o�[�̒藝�ł������B A,B,C = (sint)^3/{(sin(2t)sin(3t)sin(3t)}, t=2��/7�@�����̎����ł���B ���̎������g���ĉ��̊Ԃ̑������W�ׂ邱�Ƃ��ł��邾�낤�B�j
�E4���������̃K���A�Q�́A3���̕���������̃K���A�Q�ƊW���[�� ��ʂ�4���������̃K���A�Q�ƒ��ԑ̂̑Ή��}�������Ă݂��B �i�⑫�Fhttp://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12169484987�j a,b,c,d��4���������̉��Ax^2,y^2,z^2������������̉��� D�͕���������̔��ʎ��ł���BV��S4�̐��K�����Q�B
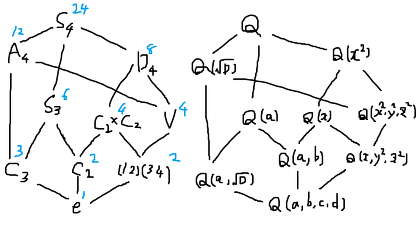
�E5���������̘b�� �E5����������BJ(Bring?Jerrard)�W���` x^5+Ax+B=0 �ɕϊ��ł��� http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11152739461 http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11150462346 http://homepage3.nifty.com/text/diary/static/Daisuugaku8.pdf http://repository.hyogo-u.ac.jp/dspace/bitstream/10132/1612/1/ZD30301003.pdf �E�L�����W����BJ�W���`�����ȕK�v�\�������� A=0 �܂��� ���̊W�����悤�ȗL����u,v�����݂��邱�Ƃ炵�� A=5u^4(4v+3)/(v^2+1), B=4u^5(2v+1)(4v+3)/(v^2+1) https://en.m.wikipedia.org/wiki/Quintic_equation#Quintics_in_Bring.E2.80.93Jerrard_form �������悭�ǂނƂ����ɏ����Ă���̂́ux^5+ax+b = 0 ������� a,b ���L�����̎��ɂ��ꂪ���ȕK�v�\�������v�ł��� �Ƃ��낪��ʂ�5���������� x^5+Ax+B = 0 �ɕϊ��������A�����L�����W���ł� A,B�͈�ʂɂ͗L�����ɂł��Ȃ��B �Ȃ̂�wikipedia�ɏ����Ă���̂́A�L�����W��5���������̂����@�ꕔ�@�Ɋւ�������ł����Ȃ��A�Ƃ������ƂɋC������(2015/11/24) [2016/2/19�NjL] ���̊Ԃ̊W 5���������̃K���A�Q��5�ʂ肠��Fhttp://www.lmfdb.org/GaloisGroup/?n=5 C5,D5,F5,A5,S5 �ňʐ��͂��ꂼ�� 5,10,20,60,120�ł���B ����a,b,c,d,e�Ƃ����BL=Q(a,b,c,d,e)�Ƃ����B �EC5�̏ꍇ Q(a)=L�ł���Ab,c,d,e��a�̑������ŕ\����B �T�^�I�ȗႪ 2cos(2��k/11) �����Ɏ��悤�ȏꍇ�� �������Ƃ��Ă� y^5+y^4-4*y^3-3*y^2+3*y+1=0 b=a^2-2, c=b^2-2, d=c^2-2, e=d^2-2 �ƊW�Â�����B �ED5�̏ꍇ ��L�f�[�^�x�[�X�ŗ��T���ƗႦ�� F(x)=x^5-5*x^2-3 f(a,b)=f(a,c)=0, g(a,d)=g(a,e)=0 �ƂȂ�悤�� y�ɂ���2���̑�����f(a,y),g(a,y)�����݂���B f(a,y)=3*y^2+(-a^4+a^3-a^2+6*a-3)*y+2*a^4+a^3-a^2-9*a-6 g(a,y)=3*y^2+(a^4-a^3+a^2-3*a+3)*y+3*a+3 c,d,e �� a,b�̑������ŕ\����B�i��̓I�ȍl�@����ɗL��B�j �EF5�̏ꍇ f(a,b)=f(a,c)=f(a,d)=f(a,e)=0 �ƂȂ�悤�� y�ɂ���4���̑�����f(a,y)�����݂��AQ(a)�W���Ŋ���ł���B �����(F(a)-F(y))/(a-y) �œ��邱�Ƃ��ł���B c,d,e �� a,b�̑������ŕ\����B �EA5�̏ꍇ f(a,b,c)=f(a,b,d)=f(a,b,e)=0 �ƂȂ�悤��3���̑����������݂�Q(a,b)�W���Ŋ���ł��� ((F(a)-F(y))/(a-y)-(F(b)-F(y))/(b-y))/(a-b) �œ�����B d,e��a,b,c�̑������ŕ\����B �ED5�̏ꍇ F(x)=x^5-5x^2-3 �̉��̊W�@�̏ڍׂȍl�@(2017/2/4) ����̍l�@�ɂ́A�㐔�̂̌v�Z�� sage online ���g�����B a��1�̗�_�Ƃ���B Q(a)�W���͈̔͂�F(x)�����������������(x-a)f_a(x)g_a(x)��3�̈��q�ɕ�������B 3f_a(y)=3*y^2+(-a^4+a^3-a^2+6*a-3)*y+2*a^4+a^3-a^2-9*a-6 3g_a(y)=3*y^2+(a^4-a^3+a^2-3*a+3)*y+3*a+3 ������f_a(y)�̗�_��b,c, g_a(y)�̗�_��d,e �Ɩ��t����B ���ɁAQ(a,b)�W����F(x)���������1�����Ɋ��S�������ȉ��̕\����F c=(a^4-a^3+a^2)/3-2a+1-b d=ab-1 e=(-a^4+a^3-a^2)/3+a-ab [�Q�l] sage online �ł̃R�}���h���͗�F K.<a> = NumberField(x^5-5*x^2-3); R.<y> = PolynomialRing(K); factor(y^5-5*y^2-3); f = 3*y^2+(-a^4+a^3-a^2+6*a-3)*y+2*a^4+a^3-a^2-9*a-6; L.<b> = K.extension(f); S.<z> = PolynomialRing(L); factor(z^5-5*z^2-3); sage online�̎g�����ɂ��Ă͗Ⴆ�F �Etsujimotter����ɂ��Љ� https://www.youtube.com/watch?v=zzvom5HfGY0 �E�l�b�g�œK���Ɍ������R�}���h�W http://fe.math.kobe-u.ac.jp/MathLibre-doc/sage-refcard/quickref/ja/quickref.pdf ------------ �K���A�QGal(L/Q)���l�@�������B�ȉ��ł͎���2�̕����Љ��B [���1] K�̊g���L�ɂ����ă�,����K�㋤���Ȃ��(��)=���ƂȂ�K-���^�ʑ� L��L �����݂��� [���2] K��M��L �ɂ�����K-���^�ʑ� M��M �� K-���^�ʑ�L��L�ɉ����ł��� L=Q(a,b,c,d,e), M=Q(a)�ŕ��2��K�p����A a���Œ肷��Gal(L/Q)�̌��́AGal(L/M)�̌������߂�Ηǂ� Q(a)��ł�b��c�������Ad��e�������ł���B ���1���b��c�����ւ���Gal(L/M)�̌������邪�A �u���^�ʑ��v�̗v���ŁAb��c�����ւ���ƁAd��e���K�R�I�ɓ���ւ�� �i����d=ab-1�ɑ���e=ae-1�̊W������j �]���āAa���Œ肷��Gal(L/Q)�̌��́A����2�ł���F �E�P���ʑ� �Eb,c�����ւ��Ad,e������ւ���B ���ɁA�Ⴆ�Aa��b�Ɉڂ�Q-���ȓ��^�ʑ����l�������B(���1��葶�݂���) �����ŁA�c��̉����ǂ��ڂ��̂����l�@���邽�߂ɂ́A f_a(y)��a��b�ɕς���2����f_b(y)�̗�_���A���̂����ǂ�2����m��K�v������B ����͎�v�Z�ł͓����sage��f_b(y)����������������Έꔭ�ł���B f_b(y)�̗�_��a,e�ł��邱�Ƃ���������B ���^�ʑ��̗v���ŁAf_a(x)�̗�_�ł���{b,c}�́Af_b(x)�̗�_�ł���{a,e}�Ɉڂ�B ����ɓ��^�ʑ��̗v���ŁAb,c�̍s��������߂��d,e�̍s���悪���܂�B a->b, b->a�Ac->e�̏ꍇ�Ad=ab-1�͌Œ�Ae=ac-1��be-1=c�Ɉڂ�B a->b, b->e�Ac->a�̏ꍇ�́Ad->c, e->d�@�ƂȂ�B a��c,d,e�Ɉڂ��ꍇ�����ꂼ�ꓯ�l�ɂ���2��������܂�B �̌��ʂׂďW�v����ƁA�L�蓾��u���͎���10�ł��邱�Ƃ�������F (abcde)(acbed)(baedc)(beacd)(cadeb)(cdabe)(dceba)(decab)(ebdca)(edbac) �����͐}�̂悤�ɒ��_�𖼕t�������܊p�`�������ɕۂϊ��Ƃ��āA ��ʑ̌QD5�ɓ��^�ł��邱�Ƃ��m�F�ł���B ���������킯�ŁAGal(L/Q)�͓�ʑ̌QD5�ɓ��^�������̂��B (�f�[�^�x�[�X�T�C�g�@http://www.lmfdb.org/NumberField/�@�Ŋm�F�ł���B)
 ���̐}�����ƂɁA���߂ĉ��̊W���l�@����B�i�ȉ��̌v�Z�ł�sage��K�v�Ƃ��Ȃ��j
�K���A�Q�̌������^�ʑ���^���邱�Ƃ���A
�u�����ʒu�W�ɂ���Γ����W�������藧�v�ƌ�����B���͂ȊW�ł���B
�]���āA2�̉�x,y���^����ꂽ���A
x,y���ׂ荇����fx(y)=0�A�ׂ荇��Ȃ���gx(y)=0 �ł���B
��f_a(y),g_a(y)��萔�{���Ď��ۂɑΏ̓I�ȊW�ł��邱�Ƃ��m�F�ł���F
3(a^2+a)f_a(y) = ay(ay+a+y-2)+3
3(a+1)g_a(y) = ay(a+y)+a^2+y^2+2a+2y+1
3g_a(y)=3*y^2+(a^4-a^3+a^2-3*a+3)*y+3*a+3�@�̒萔���ɒ��ڂ���
g_a(y)=0�̉���d,e�Ȃ̂ŁA���ƌW���̊W��� d=ab-1��B
�ό`���āAb=(d+1)/a�A���l�̈ʒu�W�� e=(a+1)/d��
���l�̈ʒu�W�� c=(b+1)/d �ł���A
��̌��ʂƍ��킹�ā@c=(b+1)/(ab-1)=(a+d+1)/ad ��
���l�̈ʒu�W�� e=(a+1)/(ab-1) ��B
�܂Ƃ߂Ĉȉ��̌��ʂ�F
�E�ׂ荇��2�̉�a,b��I�Ƃ��c��̉���
c=(b+1)/(ab-1), d=ab-1, e=(a+1)/(ab-1) �@�ƕ\�����
�E�ׂ荇��Ȃ�2�̉�a,d��I�Ƃ��c��̉���
b=(d+1)/a, c=(a+d+1)/ad, e=(a+1)/d �@�ƕ\�����
�i�������L�����\���͈�ӓI�ł͂Ȃ��̂ő��̕\�����L�蓾��j
���̐}�����ƂɁA���߂ĉ��̊W���l�@����B�i�ȉ��̌v�Z�ł�sage��K�v�Ƃ��Ȃ��j
�K���A�Q�̌������^�ʑ���^���邱�Ƃ���A
�u�����ʒu�W�ɂ���Γ����W�������藧�v�ƌ�����B���͂ȊW�ł���B
�]���āA2�̉�x,y���^����ꂽ���A
x,y���ׂ荇����fx(y)=0�A�ׂ荇��Ȃ���gx(y)=0 �ł���B
��f_a(y),g_a(y)��萔�{���Ď��ۂɑΏ̓I�ȊW�ł��邱�Ƃ��m�F�ł���F
3(a^2+a)f_a(y) = ay(ay+a+y-2)+3
3(a+1)g_a(y) = ay(a+y)+a^2+y^2+2a+2y+1
3g_a(y)=3*y^2+(a^4-a^3+a^2-3*a+3)*y+3*a+3�@�̒萔���ɒ��ڂ���
g_a(y)=0�̉���d,e�Ȃ̂ŁA���ƌW���̊W��� d=ab-1��B
�ό`���āAb=(d+1)/a�A���l�̈ʒu�W�� e=(a+1)/d��
���l�̈ʒu�W�� c=(b+1)/d �ł���A
��̌��ʂƍ��킹�ā@c=(b+1)/(ab-1)=(a+d+1)/ad ��
���l�̈ʒu�W�� e=(a+1)/(ab-1) ��B
�܂Ƃ߂Ĉȉ��̌��ʂ�F
�E�ׂ荇��2�̉�a,b��I�Ƃ��c��̉���
c=(b+1)/(ab-1), d=ab-1, e=(a+1)/(ab-1) �@�ƕ\�����
�E�ׂ荇��Ȃ�2�̉�a,d��I�Ƃ��c��̉���
b=(d+1)/a, c=(a+d+1)/ad, e=(a+1)/d �@�ƕ\�����
�i�������L�����\���͈�ӓI�ł͂Ȃ��̂ő��̕\�����L�蓾��j