内容
[1] 多項式の有限体への還元（既約性の判定法の1つ）
[2] ガロア群を求めることへの応用（Chebotarevの密度定理）
[3] 多項式の局所体への還元
[4] アイゼンシュタインの判定法との関係
[5] 問題提起

-----------------
[1] 最高次係数が1な整数係数多項式f(x)がある。

この多項式を、有限体に還元した因数分解を考えると有用な状況がある。

（有限体への還元という視点では全射 Z → Z/pZ を係数に作用させるのであるが
Z[x]を イデアルpZ[x] で割った剰余環へ全射したものを考えると考えても良いと思う）

計算としては大雑把には「mod p で考える」ということになる
具体的には例えば
x^4-2x^3+4x^2-5x+3 ≡ (x+1)(x^3+2x^2+2x+3) (mod 5)
（この多項式の由来は下記URL先の多項式を展開したものである）

初等的な有用性として、既約性の判定に使えることがある。
f(x)が整数係数でg(x)h(x)と分解できるなら mod pをとっても相応して分解できる
対偶的に、mod p で既約であれば、整数係数としても既約である。
そこで、mod pでの既約判定は、候補が有限なので判定が有限的である。

http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q10158597070
===================
次の話で分かることには、
この方法で既約だと判定できる素数がいつでも存在するとは限らない。
具体的には、f(x)が既約な4次式の場合、
その最小分解体のガロア群がC4,D4,S4の場合は、
mod p をとったときに既約となるpが必ず存在する。
一方、ガロア群がV4,A4の場合は、そのようなpは存在しない。

ただしA4の場合は、
mod p の還元で(2次式)*(2次式)と分解される素数と
(1次式)*(3次式)と分解される素数が存在することから
大域的には因数分解されないことが言える

V4の例：x^4+1
A4の例：x^4-7x^2-3x+1
LMFDB というデータベースサイトがおすすめ

===================
[2] 多項式が与えられた時にその最小分解体のガロア群を求めることについて

http://www.jmilne.org/math/CourseNotes/ant.html
第8章に
Computing Galois groups (the hard way)
Computing Galois groups (the easy way)
として非現実的な方法と現実的な方法の２つが紹介されている。
1つ目の方法は計算量が非現実的であるが
原理的に代数的にガロア群を求められるので興味深い
2つ目の方法が、mod pへの還元を利用する方法なのである。

-------------
既約な4次式によるガロア群は4種類有り得る：C4,V4,D4,A4,S4
それぞれの群をS4の部分群とみなして共役類のパターンを書き出しておく

C4の共役類
1*(1111)
1*(22)
2*(4)

V4の共役類
1*(1111)
3*(22)

D4の共役類
1*(1111)
2*(211)
3*(22)
2*(4)

A4 の共役類：
1*(1111)
3*(22)
8*(31)

S4の共役類
(1111)
6*(211)
3*(22)
8*(31)
6*(4)

意味を軽く説明する。
S4が、4つの元を置換する方法すべて(24種類)による群であり
すべてを動かさない単位元が(1111)に相当する
2つの元を交換する置換が6種類あるのを2*(211)と表記した
2つの元を交換しつつ残りの2つの元も交換する置換が3種類、
1つの元を固定して残りの3つの元を置換するのが8種類、
4つの元を巡回的に置換するのが6種類あるのが残りの記述である。
その中から部分群をなす集合を取り出したのがC4,V4,D4,A4に相当する。

一方、
多項式 x^4-2x^3+4x^2-5x+3 を mod p で因数分解した様子を書き出してみる

p=2: 既約
p=3: (x)(x+1)(x^2+1)
p=5: (x+1)(x^3+2x^2+2x+3)
p=7: (x-4)*3次
p=11 既約
p=13 既約
p=17 (x-3)(x-12)(x^2+13x+10)
p=19 既約
p=23 既約
p=29 既約
p=31 (x-19)*3次
p=37 既約
p=41,47,53,59,61 : 1次*3次
p=67 (x^2+2x+16)(x^2+63x+63)
p=71 (x-16)(x-28)(x^2+27x+22)
p=73 (x^2+35x+9)(x^2+36x+49)
p=79 1*3
p=83 1*1*2
p=89 1*3
p=97 2*2

4つの1次式に分解されるものを[1111]
2次、1次、1次と分解されるものを[211]
2次と2次に分解されるものを[22]
1次と3次に分解されるものを[31]
既約となるものを[4]
と呼ぶことにする
この5パターンを与える素数の個数の比が、
調査対象を大きくしていけば、
対応するガロア群の共役類の比に近づく
という主張が「Chebotarevの密度定理」である。

ということは4つの1次式に分解されるようなmod pが存在する
調査を続けると確かに
p=151 で (x-5)(x-93)(x-102)(x-104)と分解された

p≦151までの各パターンの集計をしてみると
[1111]:[211]:[22]:[31]:[4] = 1:8:4:13:7 であり
1:6:3:8:6 という比に確かにそこそこ近い

-------------
参考：上記の調査に使ったmaximaの入力例

p:97;primep(p);
for i:1 thru p do
if mod(g(i),p)=0 then print(i);

for i:1 thru p do
for j:1 thru p do
[h:divide(g(x),x^2+i*x+j)[2],
h1:mod(ev(h,x=0),p),
h2:mod(diff(h,x),p),
if [h1,h2]=[0,0]
 then print([i,j])
];
===================
===================

[3] 多項式の局所体への還元

「局所体への還元」というものを考えることも時に有用となる

正確な言葉で述べると煩雑になるので後の例を参考にして欲しい
「各係数がpで割り切れる回数をプロットして、
それらを含む下に凸な折れ線を描くときに
p進体における解はその傾きに対応する「付値」を持つ」

この折れ線はニュートン多角形と呼ばれる
https://en.wikipedia.org/wiki/Newton_polygon

例えば図のようなニュートン多角形を与える例を考える。

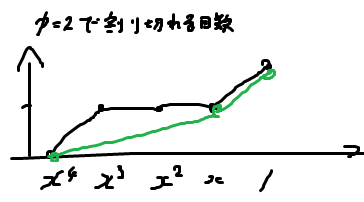f(x) = x^4+2x^3+2x^2+2x+4, p=2
ニュートン多角形は傾き1/3が長さ3、傾き1が長さ1となっている。
これによって言えることには・・
------------
準備として

「pで割り切れる回数」は通常は整数に対して定義されるが、
代数的な数αに対しても、αがpで割り切れる回数v(α)を考えたい
v(αβ)=v(α)v(β), v(α)+v(β)≧min{v(α),v(β)}
等の成立が成り立つことを期待したいが、この延長は、実際に可能である。
ただしv(α)は一般には整数ではなく有理数範囲となる。
分かりやすい例では p=2のとき v(√2)=1/2
もう少し自明でない例では　v(1+√3)=1/2, v(1+√5)=1 [いずれもp=2で]
一般的にどうするのかをうまく説明するには私の理解が十分でない

αが有理数⇒v(α)は整数　なので
v(α)が整数でない⇒αは有理数ではない
------------
「f(x)の解をa,b,c,dとしたときに、v(a)=v(b)=v(c)=1/3, v(d)=1 となっている」
ということである。

これよりさらに言えることには、
「この形のニュートン多角形を与える多項式は、既約であるか、
さもなければ1次*3次に分解されてその3次式は既約である」

なぜなら v(a)やv(ab)は整数ではないからである
=============

実際に解のp進展開を紹介すると実感が持ちやすいかもしれない

f(x) = x^4+2x^3+2x^2+2x+4　の解を2進展開すると次のようになる。
x = 2+2^3+2^5+2^9+2^11+...
x = 2^(1/3)+2^(2/3)+2^(4/3)+2^(5/3)+2^2+2^3+2^4+2^(17/3)+...

残りの2つの解は不分岐拡大が必要になるのであるが、
大雑把に 2^(1/3) の代わりに (-1±√-3)/2*2^(1/3)とおいたものが残り2つの解である

このような展開の得かたとしては、
f(2^(1/3)+...) が2でできるたくさん割り切れるように項を補正していけば良い
（もちろん手計算では辛いのでコンピュータを使っている）
うまく追加していけば望む回数以上2で割り切れるようにできる
ということがヘンゼルの補題により保証される

===============
[4] アイゼンシュタイン多項式の条件では、
ニュートン多角形は傾き1/nが長さnとなる

解をαなどとおくと v(α)はすべて1/nとなる
（局所体において分岐指数nの解をn個持つ）

このことから上記の視点により多項式は既約だということになるのである

従って、アイゼンシュタインの判定法で判定できるような多項式というのは、
対応する拡大において完全分岐するような素イデアルが存在する場合　なのである。
従ってアイゼンシュタインの判定法が適用できる多項式は結構限られている。

================
[5] 問題提起

例えば f(x)=x^4-x^3+4x^2-15x+15 はガロア群がV4であり
（※ちなみにf(x)の零点の１つは x={(1-√21)+(√15+√35)√-1}/4 ）
有限体に還元して既約になるような法が存在しないし
完全分岐する素イデアルも存在しないので
それらを利用して既約判定することができない
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11158678411

議論の中で、次のような解決を見つけることができた：

f(x)≡(x^2+6x+10)(x^2+16x+13) (mod 23) であり
これらの2次式は mod 23 で既約である

ところが(元の)定数項15からの2つの整数の積への分解は
どの組み合わせも23を法として10と13にはできない
従って大域的な2次式への分解は不可能である

「・・　おお　なるほど
定数項の約数が限られていることを組み合わせることで
より広い既約判定が可能になるのですね」

---------------
[追記1]
pで割り切れる回数v(a)の代数的数への延長に関して。
p=5, a=2+√-1 のとき v(a) はいくつだろうか。
v(a)を代数的数に延長する時には、
[a] 先にp進体Qpに延長してから代数拡大をする視点と
[b] 先に代数拡大をしてから付値をとる視点があり得る
[a] の場合は、2乗して-1になる数はQpに既に2つ存在し、
それらはそれぞれ 2+5+2*5^2+5^3+... , 3+3*5+2*5^2+3*5^3+... と展開される。
v(a)の値は√-1 としてどちらを採用するかによって0か1となる
[b] の場合は先に代数拡大Q(√-1)をとってしまうと5はもはや素元でない。
従ってQ(√-1)で5に関する付値を定めようとすることは
Q上で合成数6に関する付値を定めようとするのと同じぐらい無意味になってしまう。
------------
[追記2]
一方、関連記事Cohn の判定法に出会った。
https://en.wikipedia.org/wiki/Cohn's_irreducibility_criterion
しかもBunyakovskiの予想が保証することには
この判定法は任意の既約多項式に適用できる

[5]で問題提起した多項式 f(x) = x^4-x^3+4x^2-15x+15 では
x-2 = y とおいて係数を正にできる F(y) = y^4+7y^3+22y^2+21y+9
Cohnの判定法によれば、23以上の自然数bでF(b)が素数になるものがあれば
F(y)が既約だということができるらしい

そのようなbを人間的に探すのは困難であるが、実際 F(74)=32945179 が素数である