[0] 簡単なもの ・円柱を平面で切った図形の短直径は常に一定だから、主張は成り立つ。 ・球は傾けても水面の形が変わらないから、主張は成り立つ。 ・回転楕円体は、z軸方向に伸縮すれば球になる。 z軸方向の伸縮は短直径の長さを変えず、体積への効果は傾け具合によらず定数倍だから。主張は成り立つ。
[1] 円錐の場合に昔考えた方法。 水の体積が一定であることを利用するからこの図形「斜円錐」の体積を考える必要がある。 (底面積)*(高さ)/3 = (短直径)*(長直径)*(高さ)π/12 = (短直径)*(長直径と母線がなす三角形)π/6 と体積の計算式を変形できることに注目する。 円錐の方程式を z^2=k(x^2+y^2) とおく。 しかし[0]の回転楕円体と同様の議論により、k=1の場合を考えれば十分である。 bを定数として、z^2=x^2+y^2+b^2で表される曲面（紫）を考える。 平面（赤）がこの曲面に接していれば、短直径の長さは一定で、長直径と母線がなす三角形の面積も一定で、 従って、平面と円錐で挟まれた体積も一定となる。
（逆に円錐とz>0で交わる任意の平面に対して、bを調整すれば紫と赤が接するようにできるから、
この事実を示せば目的の主張が成り立つことが言える。）
回転対称だから、z=ax+bが、z^2-x^2=b^2と接する状況を考えて、xz平面の問題に帰着する。
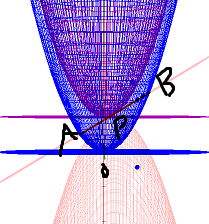
接点をP,(x,z)=(u,v)として、長直径の両端をA,B、円錐の頂点をOとおいた。
PがA,Bの中点であることと、OAとOBの積が一定であることを示したい。
（なぜならPがA,Bの中点であれば、Pを通るy軸方向の直線が短直径をなし、
Pはv^2-u^2=b^2を満たすから、Pを通るy軸方向の直線と円錐の交点は(u,±b,v)であり、
短直径の長さは2bで一定と言えるから。）
45度回転したXZ平面の直交双曲線XZ=b^2で記述する方が分かりやすい。
(X,Z)=(z-x, z+x)
(x,z)=((Z-X)/2, z=(Z+X)/2)
XZ=b^2 の点P(ab,b/a)における接線は、A(2ab,0)とB(0,2b/a)を結ぶ直線である。
これは計算しても良いし、
点(b,b)で直線x+z=2bが接している図形をX軸方向にa倍、Z軸方向に1/a倍伸縮させたものを考えても良い。
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14121258154
このことから、PがA,Bの中点であることと、OAとOBの積が一定であることがどちらも従い、考察が完了する。
[2] 放物線の場合の考察 先と同様の議論で、z=x^2+y^2の場合を考えれば十分である。 今度も、bを定数として、z=x^2+y^2+bで表される曲面（図の紫）を考えると、 平面（図の赤）がこの曲面に接していれば、短直径の長さは一定で、長直径と放物線で囲まれた面積も一定で、 従って（？）平面と円錐で挟まれた体積も一定となる。 ＊（？）を付けたのは、円錐のときに行ったような体積の変形がそれほど自明でないからである。 しかし次に書くもっと良い方法を見つけたので、これについてはもう踏み込まない。 先と同様にxz平面で考えると、以下が成り立つ： 接点をP,(x,z)=(u,u^2+b)として、接線と放物線z=x^2の交点をA,B、放物線の頂点をOとおいた。 PがA,Bの中点であることと、放物線AOBと直線ABで挟まれた面積が一定である。
これはカヴァリエリの原理的な座標変換のトリックで説明することができる。
xz平面で 放物線C1:z=x^2, C2:z=x^2+b, およびC2に接する直線L:z=2ux-u^2+b を考える。
(X,Z) = (x,z-x^2) という座標変換を考える。
そうするとC1,C2,Lはそれぞれ C1':z=0, C2':z=b, L':z=b-(x-u)^2 に変換される。（図に同じ色で描いた。）
L'の方程式については、実際にLの方程式を計算して求めなくても、
2次の係数が-1であることとC2'に接することから y=b-(x-α)^2の形になることが分かる。
uを変化させたときに、C2'とL'で挟まれた図形はx軸方向に平行移動するだけなので面積一定である。
この座標変換は（カヴァリエリの原理的に）面積を保つから、C2とLで挟まれた図形も面積一定である。
また、A,Bは放物線L'のz座標が同じ2点だから、
それらのx座標の中点は、頂点のx座標、すなわちL'とC2'の接点のx座標、すなわちPのx座標に一致する。
[3] 放物線の場合のもっと良い方法 曲面S1: kz = x^2+y^2 曲面S2: kz = x^2+y^2+b 平面H: kz = 2ux-u^2+b を考える。S2とHは接する。 （先の議論からk=1に限っても良いが数式はそれほど変わらないのでkのままにした。） ここで空間図形ごと (X,Y,Z) = (x,y,z-(x^2+y^2)/k) (x,y,z) = (X,Y,Z+(X^2+Y^2)/k) と変数変換すれば、これは（カヴァリエリの原理的に）体積を保ち、y軸方向の長さも保つ。 平面S1': Z = 0 平面S2': kZ = b 曲面H': kZ+X^2+Y^2 = 2uX-u^2+b^2 に変換される。 H'の方程式はkZ=b-(X-u)^2-Y^2 と変形できるが、先と同様の議論で具体的に計算しなくても分かる。 uを変化させたときに、S2'とH'で挟まれた図形はx軸方向に平行移動するだけなので体積一定である。 また、S1'とH'の交わりも常に半径√bの円なのでy軸方向の直径の長さも一定である。
[4] 円錐、回転双曲面、球、回転楕円体を統一的に扱える方法 曲面S1: k(x^2+y^2)+ z^2 = c^2 曲面S2: k(x^2+y^2)+ z^2 = b^2 平面H: kux + vz = b^2 を考える。(u,v)はku^2+v^2=b^2を満たす関係とすると、S2とHは点(x,y,z)=(u,0,v)で接する。 曲面S1はc=0,k＜0のときに円錐、c≠0ではk＞0のとき回転楕円体、k=1のとき球、k＜0のとき回転双曲面となる。 変数変換 (X,Y,Z) = ( (vx-uz)/b, y, (kux+vz)/b ) (x,y,z) = ( (vX+uZ)/b, Y, (-kuX+vZ)/b ) をする。これはヤコビ行列式は1であり体積は保たれる。y=Yなのでy軸方向の長さも保つ。 また、kx^2+z^2 = kX^2+Z^2 の関係がある。 曲面S1': k(X^2+Y^2)+Z^2 = c^2 曲面S2': k(X^2+Y^2)+Z^2 = b^2 平面H': Z = b に変換される。 今度は変換の方程式をu,vに依存させたことで、変換した結果がu,vに依存せず一定になる。 従ってS2とHで挟まれた図形の体積も、楕円のy軸方向の直径も、bだけに依存する。 ここで使った変換の挙動について踏み込んでみると、 ＊k＝1のときは回転である。 ＊k＞0のときは伸縮して球にして回転して伸縮して元に戻す変換に相当すると思う。 ＊k＜0のときは[1]で登場したXZ平面での直交双曲線に変換して、 X軸方向にa倍、Z軸方向に1/a倍伸縮させて、元に戻す変換に相当すると思う。 ＊√-kを添加した2次体と結びつけると、kx^2+z^2 = kX^2+Z^2が納得しやすい： Z+X√-k = (z+x√-k)*(v-u√-k)/b z+x√-k = (Z+X√-k)*(v+u√-k)/b
23:45 2020/05/29