[説明] 2と互いに素な素元pに対して「標準形」{p}と「補正形」p* をうまく定めると、 素元p,qに対して 「{q}がmod pで平方剰余 ⇔ p* がmod qで平方剰余」・・・★ という相互法則を成り立たせることができる。 通常の整数環では、{p}は±pのうち正のほう、p*は±pのうち(p*)≡1 (mod 4)を満たすほうと定めると★の形となる。 虚二次体Q(√d), d=-1,-2,-3,-7 の場合について試行錯誤して、 次のように定義すれば、★が成り立つことを上記のスクリプトで観察した。（証明はしていない） [d=-1] [y^2=x^3+x] {q}は ±p,±ipのうち、{q}≡1 (mod 2+2i) となるもの。 p*は{p}と同じ [d=-2 isogeny aの場合] [y^2 = x^3+x^2-3x+1] {q}は±qのうち、{q}≡1,3, -1±√-2,-3±√-2,-1+2√-2,-3+2√-2 (mod 4√-2) となるほう p*は、±p,±p√-2 のうち、 p*≡1,-1+2√-2 (mod 4) または p*≡2±√-2,2±3√-2 (mod 4√-2) となるもの。 [d=-2 isogeny dの場合] [y^2 = x^3-x^2-3x-1] {q}は±qのうち、{q}≡1,3,1±√-2,3±√-2,-1+2√-2,-3+2√-2 (mod 4√-2) となるほう p*は、±p,±p√-2 のうち、 p*≡1,-1+2√-2 (mod 4) または p*≡-2±√-2,-2±3√-2 (mod 8) となるもの。 [d=-3] [y^2+y=x^3] {q}は±qのうち、{q}≡1 (mod √-3) となるほう p*は、±p,±p√-3 のうち、 p*≡1,-1+2√-3 (mod 4)となるもの。 [d=-7] [y^2+xy=x^3-x^2-2x-1] {q}は±qのうち、 {q}≡1,2,4 (mod √-7) となるほう。 p*は、±p,±p√-7 のうち、 p*≡1,-1+2√-7 (mod 4)となるもの。 [補足] ・d=-3,-7のときQ(√-d)の整数環は {a+b√d | a,bは整数} ではない。 a,bが共に半整数、という元もある。 d=-3 のときは (-1+√-3)/2 を1回か2回掛ければa,bを整数にできる。 d=-7 のときは a,bが共に半整数のとき、ノルムが偶数となる。 なので"奇素数"に関する相互法則を観察するにはa,bは整数で十分であった。 （半整数を実装するのが面倒だったのが本音。） ・p/qの計算は、qのノルムN(q)を計算して、p^[N(q)-1/2] mod q を計算している。 なのでqが素元でない場合には、この値は信用できない。[参考値]と表示した。 d=-1,-2,-3,-7以外の場合は素元判定を実装していないので常に[参考値]と表示した。
この非対称的な相互法則の形は、類体論的な視点による： Kの整数環Oのイデアルpに対して、 L/Kのガロア群が(O/p)*に一致し、「素イデアルqがL/Kで完全分解する ⇔ {q}≡1 (mod p)」 を満たすようなアーベル拡大L/Kが存在する（射影類体） pが素イデアルのとき、(O/p)*は巡回群であり、指数2の部分群が1つだけ存在する。それをHとする。 対応する中間体K⊂M⊂Lで、M/Kが2次拡大のものが存在し、それが M=K(√p*) という関係である。 そうして、「素イデアルqがM/Kで完全分解する ⇔ {q}∈H 」という状況となる。 qがM/Kで完全分解するとは、p*がmod qで平方剰余であるということであり、 {q}∈H とは、すなわち{q}がmod pで平方剰余であるということである。 K=Qのときは、L/Kは、1の原始p乗根を付け加えて得られた。 Kが類数1の虚二次体Q(√-d)のときは、大抵、L/Kは対応する虚数乗法を持つ楕円曲線のp等分点の座標を付け加えて得られる。 これは経験的にどうやらそうなるらしいという感触で、根拠が無いし、実際、例外を発見した。（それで「大抵」と書いた） K=Q(√-2)のとき楕円曲線の原始4√-2等分点は16個あるが、その16次式は2つの8次式に分解する。後で登場する。複雑。 次に、標準形{q}の定義を明らかにする必要がある。 「フロベニウスのトレース」が1つの説明となった。根拠は確かでないが、うまくいっている。 N(q)をqのノルムとする。 (x,y)のq倍点、-q倍点のうち、どちらかが、(x^N(q),y^N(q))に合同になる。 すなわち (x^N(q),y^N(q)) ≡ (x,y)の{q}倍点 (mod q) となるように{q}を定めることができる。 これを直接調べるのは手間がかかるが、Q(√d)/Qで分解する素元qについては、 対応する楕円曲線のモジュラー形式のq展開の係数が、{q}のトレースの符号に一致する方として、データベースを利用できる。 ところが「対応する虚数乗法を持つ楕円曲線」というところがまた一意的でない。 Q(√-2)に対応する楕円曲線を得るには、例えばj(√-2)=8000だから、 http://www.lmfdb.org/EllipticCurve/Q/ のj-invariantに8000を入れて検索すれば良い。 そうすると、conductorが最小のものがある意味で「標準的」だと思われるが、 それでもd=-2の場合は、conductorが最小なisogeny class が2つあった。(a,dと名付けられている) http://www.lmfdb.org/EllipticCurve/Q/256/a/ q-2q^3+q^9-6q^11-6q^17-2q^19-5q^25+4q^27+12q^33+6q^41+10q^43-... http://www.lmfdb.org/EllipticCurve/Q/256/d/ q+2q^3+q^9+6q^11-6q^17+2q^19-5q^25-4q^27+12q^33+6q^41-10q^43-...
やや唐突であるが、O/(4√-2) の既約剰余類は16個あり、乗法群はZ/4Z×Z/2Z×Z/2Zの構造をしていて 位数4,2,2の生成元として a=1+√-2, b=-1, c=5 をとることができる。 G = {e,a,aa,aaa, b,ab,aab,aaab, c,ac,aac,aaac, bc,abc,aabc,aaabc} 原始4√-2等分点の1つをPとおくと、16個の原始4√-2等分点は、そのg倍点(g∈G)である。 その16個のy座標が満たす方程式は、2つの8次式に分解する結果であった。 16個のうち、8個のy座標が、その8次式の解となる。 それを調べると、 isogeny a では {e,bc,ab,ac,aa,aabc,aaab,aaac} isogeny d では {e,bc,a,a,aa,aabc,aaa,aaa} であった。 a=1+√-2, b=-1, c=5 を使って既約剰余類の形で書くと isogeny a では {1,3,-1±√-2,-3±√-2,-1+2√-2,-3+2√-2} (mod 4√-2) isogeny d では {1,3,1±√-2,3±√-2,-1+2√-2,-3+2√-2} (mod 4√-2)
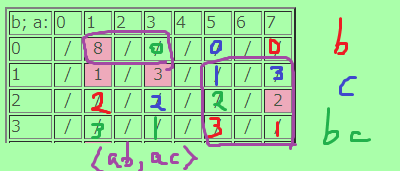赤のkという数字はa^k*b、青のkという数字はa^k*c、緑のkという数字はa^k*bcを表す。
isogeny a の部分群は紫で囲った枠である。
これが、「フロベニウスのトレース」と結びつくことを観察した。
ノルムNの素元qに対して、{q}が上記部分群に属するように{q}=±qの符号を選ぶ。
ノルムが3,11,17,19,41,43の素元q=-1+w,3+w,3+2w,-1+3w,-3+4w,5+3wに対応する標準形{q}が、
isogeny a の場合 -1+w, -3-w, -3-2w, -1+3w, 3-4w, 5+3w
isogeny d の場合 1-w, 3+w, -3-2w, 1-3w, 3-4w, -5-3w
これらのトレースが実際先のページのModular formの係数に対応していることが観察できる。
isogeny a: q-2q^3+q^9-6q^11-6q^17-2q^19-5q^25+4q^27+12q^33+6q^41+10q^43-...
isogeny d: q+2q^3+q^9+6q^11-6q^17+2q^19-5q^25-4q^27+12q^33+6q^41-10q^43-...
(これの3,11,17,19,41,43次の係数の符号を、標準形の実部の符号と比較)
これはこれで、これが射影類体である。
ここには指数2の部分群が3つあるから、平方剰余の法則が3つ導出できる。
部分群{e,ab,aa,aaab}={1,-1-w,-1+2w,-3-w}に対しては、
これらのy座標の和が生成する2次拡大を計算すると、 K(√-w) である(PARI/GP使用;末尾参照)
従って素イデアルの分解の法則から
{q}≡1,-1-w,-1+2w,-3-w (mod 4w) ⇔ -wがmod qで平方剰余
{q}≡3,-1+w,-3+2w,-3+w (mod 4) ⇔ -wがmod qで平方非剰余
部分群{e,ac,aa,aaac}にはK(√w)
部分群{e,bc,aa,aabc}にはK(√-1)=K(√2) が対応する。
スクリプトの「{q}/p,p/qを表示」モードはこれの観察のための実装である。
-----------
isogeny class d を採用した場合、{q}∈[付録] ・周辺 関連して、志村の相互法則というのがあるらしい。難しい。 初めて多項式の素因数集合の性質に出会った時のことと似ている・・ ・実は、最初の考察では、conductorが最小でないものを使っていた。 ワイエルシュトラスの標準形を使っていた。y^2=x^3-30*x-56 である。 conductorは3を素因子に持つものとなる。せっかくなのでその場合の結果も書いておく。 これを使った場合、標準形と補正は次のように定めると辻褄が合った： q≡±1 (mod 3) ならば {q}≡1,3, -1±w,-3+2w (mod 4w) q≡±w (mod 3) ならば {q}≡-1,-3, 1±w,3+2w (mod 4w) {p}≡±1+w (mod 4) ならば p* = 3w{p} {p}≡±1-w (mod 4) ならば p* = -3w{p} {p}≡1,-1+2w (mod 4) ならば p* = {p} {p}≡1+2w,3 (mod 4) ならば p* = -{p} 3で割った余りが登場するのはそういう事情だったのだと納得した。 「ツイスト」という言葉が合うかもしれないが分からない。 ・PARI/GPでによるisogeny aの場合のコマンド。 E = ellinit([0,1,0,-3,1]) F = x^3+E[2]*x^2+E[4]*x+E[5]-y^2-E[1]*x*y-E[3]*y z = [x,y] q = quadgen(-8) ellmul(E,z,4*q)[1] denominator(%) polresultant(%,F,x) factor(%) Fy = %[5,1] // Fy, 4w等分点のy座標のうち8個が満たす方程式 factornf(F,Fy) p = [ x-%[1,1], Mod(y,Fy) ] // a=1+q, b=-1, c=5 pa = ellmul(E,p,1+q) paa = ellmul(E,pa,1+q) paaa = ellmul(E,paa,1+q) pb = ellmul(E,p,-1) pc = ellmul(E,p,5) pbc = ellmul(E,p,3) pab = ellmul(E,pa,-1) pac = ellmul(E,pa,5) pabc = ellmul(E,pa,3) paab = ellmul(E,paa,-1) paac = ellmul(E,paa,5) paabc = ellmul(E,paa,3) paaab = ellmul(E,paaa,-1) paaac = ellmul(E,paaa,5) paaabc = ellmul(E,paaa,3) subst(Fy,y,pa[2]) subst(Fy,y,pac[2]) // a倍点やac倍点がFyの零点かどうか調べられる u1 = p[2]+pab[2]+paa[2]+paaab[2] u2 = pbc[2]+pac[2]+paabc[2]+paaac[2] lift ((u1+u2)^2/4 - u1*u2) // 256+64*wを出力。部分群{e,ab,aa,aaab}に対応する中間体がK(√256+64*w)だと分かる。 15:48 2019/01/06