しばらく前に、楕円曲線の等分点と関連した描写をした。(http://searial.web.fc2.com/aerile_re/qheihou.html) そこでは状況証拠から法則を推測し描写した。 今回は、類体論の結果を使い、根拠がしっかりしている。 ＊類体論の結果の証明については触れられない。 ＊楕円曲線との関連は明らかにできていない。 p進数の概念にはある程度なじみがあることを想定する。 ガロア理論は既知と想定する。 特に現象を観察し描写するという態度を心がけた。 最後にLubin-Tate理論の勉強メモも書いたけど読んで役に立つものな気はあまりしない。
＜Qの大域アルティン写像の具体的な描写＞ QのイデールをA*とおく。イデールの定義はどこかで知っているものとする。 A*の元aは a=(a2,a3,a5,...,ar) [a2∈Q_2*,a3∈Q_3*,a5∈Q_5*,ar∈R*] というふうに記述できる。 （イデールの定義より、a2,a3,a5,.., のうち単数でないものは有限個） （Q_p*の単数とは、pと互いに素なp進整数のことを指している。） Qの最大アーベル拡大Q^ab/Qのガロア群をG_abとおく。 G_abの元gを記述するには、 すべての有限次アーベル拡大L/Kに対して、gがどう作用するのかを記述する必要がある Qの場合は、Q_abはすべての円分拡大を合わせたものだから、 色々なnに対して、gが1のn乗根に対してどう作用するのかを記述するのが1つの方法となる。 アルティン写像(θと呼ぶ)とは、A*からG_abへの準同型（とみなすことができる）。 どのような写像か、例を挙げる。 ・A*の元 a=(1,1,1/3,1,1,...)の場合(Q_5成分のみが1/3で他が1) θ(a)は、1の原始5乗根ζ_5 をその3乗に移す。 5と互いに素なnに対する1の原始n乗根は、固定する。 ・A*の元 a=(1,1,5,1,1,...)の場合(Q_5成分のみが5) θ(a)は、1の原始5^k乗根は固定する。 5と互いに素なnに対しては1の原始n乗根をその5乗に移す。 （「p=5に関する（算術的）フロベニウス写像」とも言えるような元である） ・一般の場合を描写する a∈A*のQ_p成分のみがa_p≠1で、他の成分がすべて1のとき、 [場合1：a_pが単数の場合] θ(a)は、1の原始p^n乗根を、そのx乗に移す。 ここで xは、x*a_p≡1 (mod p^n)で定まる剰余類として定める。 pと互いに素な1の冪根は固定する。 [場合2：a_p=p の場合] θ(a)は、1の原始p^n乗根を固定する。 pと互いに素な1の冪根を、そのp乗に移す。 ・無限成分のみ1でない場合 a=(1,1,1,...,ar)の場合 θ(a)は、arが正の時は恒等写像、arが負の時は複素共役写像である。 ・これらの積をとることで、任意のイデールの元aに対するθ(a)が描写できる。 ・例えば a=(2,2,2,...,2) [すべての成分が2] に対するθ(a)を考える。 1の原始2^k乗根への作用は、すべての成分とも恒等写像である。 奇素数pに対する1の原始p乗根への作用で恒等写像でないのは2つである： Q_2成分が、1の原始p乗根を2乗する。 Q_p成分が、1の原始p乗根をx乗する。xは2の逆元である。 ということは、θ(a)は1の原始p乗根も固定する。 同様にして、任意の有理数qに対して a=(q,q,q,...) に対するθ(a)は恒等写像である。 θの核は、本質的にこれですべてであるというのが類体論の重要な結果の1つである： kerθ = {(a,a,a,...,ar)|ar>0 }・・・★ [すべての有限素点成分が同一の有理数で、無限素点成分が正の実数、という部分群] （これは、一般の体Kに対するアルティン写像の場合では、 すべての有限素点成分が同一のK*の元で、無限素点成分では単位元の連結成分 と一般化される。） 従って A*/kerθ と G_ab は同型ということになる。 この同型をより精密に述べるのがノルムを使った視点であるが 言葉の定義がいくつか必要で、今回の目的には必要ないので省略する （局所のときのこれに相当する視点が後で登場し、重要な役割をする。）
＜局所アルティン写像＞ 大域アルティン写像を、局所アルティン写像θ_pの積としてとらえることを描写する。 θ_pは、Q_p* から Gal(Q_p^ab/Q_p) への準同型である。 （ここで「Q_pはQの拡大体」であることに注意すると、Q^abはQ_p^abに埋め込める。 中間体 Q⊂L⊂Q^ab に対しても、Q⊂L⊂Q_p^ab の包含がある。 そういうわけで、Q_p^abの自己同型の定義域をQ_p^abからQ^abに制限することで、 Gal(Q_p^ab/Q_p)の元からGal(Q^ab/Q)の元が自然に誘導される。 こうして、各θ_p(a_p)の像を、Gal(Q^ab/Q)の元としてを掛け合わせる操作が可能となり、 「大域アルティン写像は局所アルティン写像の積」という描写が可能となる。） 記述を簡単にするため、以下ではpは有限素点とする。 また、今回の目的のため、Q_pに限らずQ_pの有限次拡大K_pをも想定する。 ★に相当する局所の類体論の結果は次のようになる： 「θ_p: K_p*→Gal(K_p^ab)の核は、単位元である。」 すなわち K_pの指数有限な開部分群U と 有限次アーベル拡大L/K_pが1対1に対応する。 （「指数有限な開部分群」とはこの場合は具体的には、 U={x|x≡a1,a2,... (mod f)} のような形で書ける部分群のことである） この対応をより精密に述べる、次のノルムの視点がある： 「部分群Uは、対応する拡大L/K_pのノルム写像 L*→K_p* の像に一致する」 （ノルム写像とは、共役の積である） 局所アルティン写像の定義は少し後で登場する。 上記のノルムの性質から逆に局所アルティン写像を知ることもできて、後ではそれを使う。
＜局所体の代数拡大の様子＞ ・Q_3の2次拡大は3つある。それぞれ、√-1,√-3,√3を添加する拡大である ノルム写像の像であるQ_3*の指数2の部分群を具体的に描写すると次のようになっている。 {a^2+b^2|a,b∈Q_3} = (9Z±1)*9^Z = {1,2,4,5,7,8,9...} {a^2+3b^2|a,b∈Q_3} = (3Z+1)*3^Z = {1,3,4,7,9,10...} {a^2-3b^2|a,b∈Q_3} = (3Z+1)*(-3)^Z ={1,4,6,7,9,10...} 分岐拡大と不分岐拡大に分けて考えるのがよい。 このノートで中心となる2次拡大の場合、分岐拡大は完全分岐拡大である。 ・Q_3(√-1)/Q_3 のような拡大が不分岐拡大である。 極大イデアルは分解せず、剰余体が拡大する。(F_3からF_9になっている。) ノルム写像の像は、素元を含まず、単数の全部を含む。 局所体の不分岐拡大は、各次数に対して1つしかない。 ・Q_3(√3)/Q_3 のような拡大が分岐拡大である。 極大イデアルが分解し、剰余体は同じままとなる。 ノルム写像の像は、素元(pで1回だけ割り切れる元)を含み、単数の半分を含む。 局所体の分岐拡大は、有限個だが大抵複数ある。 (http://www.lmfdb.org/LocalNumberField/ にデータベースがある) ・Q_2の2次拡大は7個もある。 対応する指数2の部分群Uを整理して記述する方法として Q_2*/Q_2*^2 の様子を使うのが1つの方法である。 平方元は常にUに属するから、平方元倍を同一視した同値類で考えるわけである。 Q_2*^2 = (8で割った余りが1)*2^(2Z) と書けるから、 a,bが奇数なら a≡b (mod 8) のとき a≡b (mod Q_2*^2) であり、 Q_2*/Q_2*^2 の代表元として例えば {±1,±5,±2,±10} をとることができる 2次の不分岐拡大に対応する部分群は、{±1,±5}である。（Q_2(√5)に対応） 分岐拡大に対応する部分群が持つ単数の組は、{±1},{1,5},{1,-5}のどれかとなる。 それぞれに対して、{±2,±10}のほうから剰余類を選ぶ方法が2種類ずつある。具体的には： Q_2(√2) -- {±1,±2} Q_2(√10) -- {±1,±10} Q_2(√-2) -- {1,-5,2,-10} Q_2(√-10) -- {1,-5,-2,10} Q_2(√-1) -- {1,5,2,10} Q_2(√-5) -- {1,5,-2,-10} [注意] 例えばQ_2(√-6) とQ_2(√10) は同型である。 10/(-6)=-5/3=-15/9はQ_2では平方元であり、つまり√10=k√-6となるk∈Q_2が存在する。 こう考えると、Q_2の2次拡大を挙げるときも上記の代表元を使うことが有効で、 それらはQ(√d), dは{±1,±5,±2,±10}のうち1以外の元、で挙げつくせる。 ・さらに、Kw=Q_2(√-2)の2次拡大を今回特に考えたい。このノートを通して√-2=wと表記する。 Kw*/Kw*^2 の様子は、さらに入り組んでいる。[調べる方法は後の補足参照] Kw*^2 ≡ (4wで割った余りが1か(-1+2w))*w^(2Z) と書けて、 a,bがwと互いに素なら a≡b (mod 4w) なら a≡b (mod Kw*^2) であることが分かり、 Kw*/Kw*^2 の代表元には、{±1,±5,±(1+w),±5(1+w),±w,±5w,±w(1+w),±5w(1+w)} がとれる。 wと互いに素なx+yw を{±1,±5,±(1+w),±5(1+w)}の積で表した様子を示しておく[図のa=1+w]：
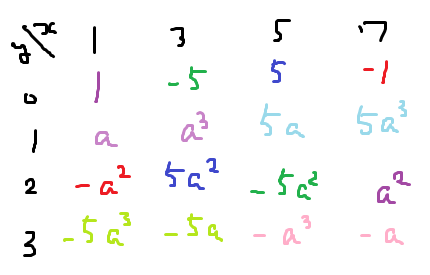なのでKの2次拡大は15個もある。そのうちのいくつかの対応を示す：
Kw(√5) -- {±1,±5,±a,±5a} (不分岐拡大)
Kw(√-1) -- {±1,±5,±w,±5w}
Kw(√-5) -- {±1,±5,±aw,±5aw}
Kw(√a) -- {1,5,-a,-5a,-w,-5w,aw,5aw}
Kw(√-a) -- {1,5,a,5a,-w,-5w,-aw,-5aw}
Kw(√w) -- {±1,±5a,±w,±5w}
Kw(√-w) -- {±1,±a,±w,±aw}
（１つの法則として、dがwと互いに素ならx=1,y=2のときx^2-dy^2≡5となるので
dがwと互いに素ならKw(√d)に対応する部分群は5を含むことが分かる。
Kw(√d)とKw(√d')が分かれば、Kw(√dd')はそれらのXOR的な感じで得ることができる。
残りは、x^2-dy^2のx,yにいろいろ代入して取り得る値を地道に調べた。）
---
[補足]
主単数群を描写するのにp進logとexpを考える視点がある
log(1+x)=x-x^2/2+x^3/3-x^4/4+...
exp(x)=1+x+x^2/2+x^3/6+x^4/24+...
「xが2で割り切れる回数」＞1であれば、exp(x)は(p進位相で)収束する。
今回Kwの極大イデアル(w=√-2の倍数)をmとおくと、x∈m^3であれば良い。
すなわち exp:m^3 → 1+m^3 が同型となる。
特に、(m^3)に2を掛ける写像を施した像 2m^3=m^5 に対応するexpの像を考えると
1+m^3 の部分群 1+m^5 は、1+m^3を2乗した像であることが分かる。
すなわち任意のx∈1+m^5は平方元であることが分かる。
（ちなみに1+m^4では足りない。例えば5=1+w^4は平方元でない。）
これは有難い。つまりwと素なA,B∈Kw*^2に対して、
A≡B (mod m^5) ならば BはAの平方元倍であるから、Kw*/Kw*^2 の元として同一となる。
だからwと素なものについては mod m^5 の範囲で調べれば良い。
Kw*/Kw*^2の代表元は、wと素な代表元と、それらにwを1回ずつ掛けたものとなる
（インターネットで検索すると手に入る局所体の詳しい教材として
「Local Fields and Their Extensions」を紹介しておく。）
＜局所アルティン写像＞ Qの場合は、大域アルティン写像を構成的に描写した。 まず、Q_pの場合に、局所アルティン写像を構成的に描写しておく。 （Q_p^abもQ_pに1の冪根を添加して得られることが知られていることを使う） この描写は、Qの大域アルティン写像を描写する時に既に行っているものである。 θ_p: Q_p*→Gal(Q_p^ab/Q) を定める。 Q_p* の元aは、a=u*p^k [uは単数] と一意的に書かれる。 θ_p(u)とθ_p(p)を定めれば良い。 ・θ_p(u)は、1の原始p^k乗根ζをxはux≡1 (mod p^k)で定めるxによってζ^xに送り、pと素な1の原始n乗根は固定する。 ・θ_p(p)は、1の原始p^k乗根は固定し、pと素な1の原始n乗根はそのp乗に送る(算術的フロベニウス) 標語的に「uは分岐拡大に作用し、pは不分岐拡大に作用する」 [注意] それぞれを逆元として定義する流儀もあるらしい https://www.ms.u-tokyo.ac.jp/~abenori/conf/20150817/exercise.pdf の内容自体は難しいが最初の注意書きに類体論がさらっとまとめてあり、 文献によって違い得る点の注意書きが参考になるかもしれない。 --------- 次に、Q_p以外の一般の局所体Kの場合の局所アルティン写像を描写する。 （満たす性質を描写するだけで、完全な定義は与えない。） a∈K*は先と同様にa=u*π^k [uは単数]と書かれる。πは素元である。 （πの選び方には単数倍の自由があり、標準的なものは無い） θ_p(u)とθ_p(π)を定めれば良い。 θ_p(π)をやはり（算術的）フロベニウス写像として定義する； （分岐拡大には恒等写像、不分岐拡大L/Kとα∈Lに対しては、 α'≡α^p (mod π)となるαのK上共役α'に送る、という写像である。） 一方で、θ_p(u)は不分岐拡大には恒等写像で、分岐拡大に非自明に作用する。 アルティン写像を記述する際に、これを記述するのが一番難しい所になる。 素元πの選び方は標準的なものが無く、πの選び方を変えるとa=u*π^kの分解が変わる。 従って、θ_p(u)はπの選び方に依存するが、 最終的に、θ_p(a)がπの選び方に依存しないように定義される必要がある。 これを実現する方法として主に2つの方法が知られている（詳細は一旦飛ばす）： ・Lubin-Tate理論 ・ブラウアー群とコホモロジー http://www.math.titech.ac.jp/~taguchi/nihongo/cft.pdfに簡単な紹介があり、 詳しい教材としては、J.milneさんの教材https://www.jmilne.org/math/CourseNotes/cft.htmlを挙げておく。 しかし、具体的な代数拡大が先に分かっている場合は、 性質「部分群Uは、対応する拡大L/K_pのノルム写像 L*→K_p* の像に一致する」 を使って様子を知ることができる。 例えば、L=Kw(√-1)というKw有限次拡大には{±1,±5,±w,±5w}*Kw^2 という部分群が対応した。 この対応から、θ_p(±1)やθ_p(±5) は L/Kwに恒等写像として作用し θ_p(±1+w) などは、L/Kwに共役写像として作用することが分かる。
＜相互法則との関係＞ L/Kで完全分解するKの素イデアルpの条件を知りたいとする。 これは、pの上にあるLの素イデアルの1つをqとしたとき、 対応する剰余体L/qとK/pが同型になることに相当する。 ここで α=(1,1,1..,p,1,..)[p成分のみp]というイデールの元の行き先θ(α)を考える。 これは局所的にpのフロベニウスで定義されて、 フロベニウス写像の性質により、その位数は剰余体の拡大次数[L/q:K/p]に一致する。 すなわちL/qとK/pが同型であることは、フロベニウス写像の位数が1、つまり恒等写像、 つまりθ(α)がL/Kでは恒等写像であることに相当する。 まとめると pがL/Kで完全分解 ⇔ θ(α)のL/Kが恒等写像 一方、アルティン写像により、すべての成分が同一の有理数は恒等写像に送られるから、 すべての成分を同一の有理数倍に対してアルティン写像の像は不変である。 なので、α/p=(1/p,1/p,...,1,1/p,...) とおくとθ(α)=θ(α/p)である。 このθ(α/p)を局所ごとに調べると、別の側面からその像を知ることができる。 ・例えば具体的にK=Qで、Lが1の原始5乗根ζからなる体Q(ζ)のとき、 θ(α/p)はp=5の成分以外だけが非自明であり、従ってpを5で割った余りに依存する。 具体的には、θ_5(u)がL/Qで恒等写像 ⇔ u≡1 (mod 5) である。u=1/pで適用すれば p≡1 (mod 5) ⇔ θ_p(α/p)=1 ⇔ θ(α)=1 ⇔ pがL/Kで完全分解 というふうに相互法則を得ることができた。 ・K=Q(w)=Q(√-2)の例では 例えばq=3+w のときqがmod πで平方剰余になる条件を求める。 L=K(√q)で完全分解するような素イデアルπの条件である。 α=(1,..,1,π,1...)[π成分のみπ] の行き先について知りたい。 α/π=(1/π,1/π,...,1,1/π,...) の行き先を考える。 L/Kで分岐する素点(2つある。wとq。)での成分だけが非自明である。 q=3+wは、先のa=1+wを使った表を参照すると、q=3+w≡a^3≡a (mod Kw*^2)である。 従って局所Kwでのノルム写像の像は K(√a)のと同じ {1,5,-a,-5a,-w,-5w,aw,5aw} であり、 特に L/K は wで分岐していて、θ_w(π)=θ_w(1/π)は(πは"奇素数"と想定して) π≡(1,5,-a,-5a) (mod Kw*^2) のとき恒等写像、そうでないとき共役写像となる。 [πを4wで割った余りが先の表の色で描写すると 濃紫・青・ピンク・黄緑のとき恒等写像で、薄紫・水色・赤・緑のとき共役写像である] もう1つの分岐する素点qでの様子が必要である。こちらのノルム写像の像は簡単で、 x+qy^2が取り得る値だから、特にπがqと互いに素な場合を想定するなら、「平方剰余」という集合となる。 πがqを法として平方剰余ならθ_q(π)=θ_q(1/π)は恒等写像、そうでなければ共役写像である。 結果をまとめると q=3+w が mod πで平方剰余 ⇔πがK(√q)/Kで完全分解 ⇔θ(α)=1 ⇔θ(α/π)が恒等写像 ⇔θ_w(1/π)とθ_q(1/π)がともに恒等写像 または θ_w(1/π)とθ_q(1/π)がともに共役写像 ⇔（π≡濃紫・青・ピンク・黄緑 (mod 4w) かつ πがmod qで平方剰余） または （π≡薄紫・水色・赤・緑 (mod 4w) かつ πがmod qで平方剰余） というふうにして、相互法則（の1つの表現）を得ることができた。
＜Q(√-2)の相互法則の追求＞ q=3+wの場合を個別に記述したのを、一般化して、しかし具体的に描写する。 ルジャンドル記号を使う。 (q/π) は qがmod πで平方剰余のとき1、平方非剰余のとき-1、という記号である あと「π∈{...}?A:B」という3項演算子表記を使う。 （π∈{...}ならばA、そうでなければB という意味） 平方元倍を同一視して分類する表を再掲しておく。
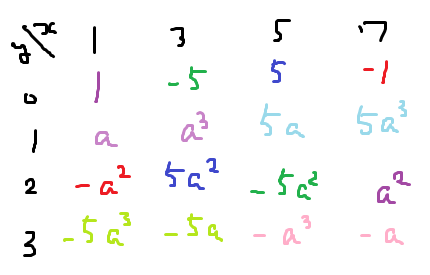補充法則
・(-1/π)＝(π∈濃い色?1:-1)＝(π≡1(mod 2)?1:-1)
余事象は π≡w (mod 2)
・(w/π)＝(π∈{濃紫・赤・水色・黄緑}?1:-1)
相互法則
・q≡青,濃紫 のとき K(√q)/Kではwが不分岐となる。例：q=5,3+2w
一番単純で、(q/π)＝(π/q) となる。
・q≡赤,緑 のとき K(√q)/Kのノルム写像の像の単数部分は{濃紫・青・赤・緑}であった。
(q/π)＝(π∈{濃紫・青・赤・緑}?(π/q):-(π/q)) と書ける。
実は前半の条件は π≡1 (mod 2) と簡単に書ける。
・q'=-q とおくとq≡青,濃紫となることを使うと理解が深まるかもしれない。
つまりq≡赤,緑 のとき
(q/π)＝(-1/π)(q'/π)＝(-1/π)(π/q') という視点である。
・q≡薄紫・水色 のとき、同様に
(q/π)＝(π∈{濃紫・青・ピンク・黄緑}?(π/q):-(π/q))
条件は、合同式では、πの虚部≡0,3w (mod 4w) という条件とでも書ける。
・q≡ピンク・黄緑 のとき
(q/π)＝(π∈{濃紫・青・薄紫・水色}?(π/q):-(π/q))
条件は、合同式では、πの虚部≡0,w (mod 4w) という条件とでも書ける。
----------------------------
＜Q(√-1) のとき＞
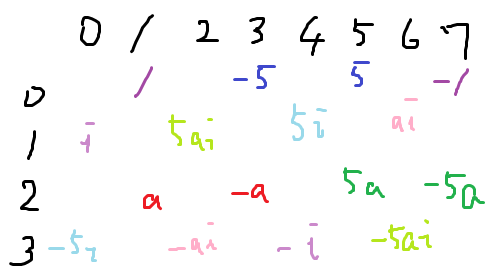補充法則
・(i/π)＝(π∈{濃紫・薄紫・青・水色}?1:-1)
＝(π≡±1,±i(mod 4)?1:-1)
[余事象はπ≡±1±2i,±2±i]
・((1+i)/π)＝(π∈{濃紫・薄紫・赤・ピンク}?1:-1)
＝(π≡±1,±(1+2i),±i,±(1+2i)i (mod 4+4i)?1:-1)
[余事象はπ≡±3,±(1-2i),±3i,±(1-2i)i]
相互法則
・q≡濃紫・青 のとき不分岐拡大 (q/π)＝(π/q)
・q≡赤・緑 のとき (q/π)＝(π∈濃い色?(π/q):-(π/q))
・qが薄い色のときは、(q/π)＝(iq'/π)とおくと補充法則と濃い色の場合に帰着する。
＜Q(√-3) のとき＞
整数環に半整数が出てくる。w=√-3,z=(1+w)/2 とおいている。
mod 4の違いを同一視していて、2+2wは"4の倍数"であることに注意。
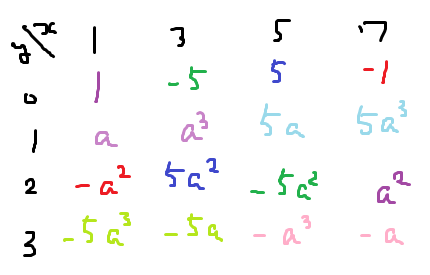補充法則
・(-1/π)＝(z/π)＝(π∈{濃紫・薄紫}?1:-1)
相互法則
・q≡濃紫のときは不分岐拡大 (q/π)＝(π/q)
・q≡薄紫のときは (q/π)＝(π∈{濃紫・薄紫}?(π/q):-(π/q))
・q≡青のときは(q/π)＝(π∈{濃紫・水色}?(π/q):-(π/q))
・q≡水色のときは(q/π)＝(π∈{濃紫・青}?(π/q):-(π/q))
＜Lubin-Tate理論＞ さっき紹介したJ.milneさんの教材の要点まとめ的なものを書いた。 [memo] http://math.bu.edu/people/jsweinst/FRGLecture.pdf の5ページには圏論的な視点での形式群の描写に出会った。難しい。 ・形式群 K:局所体, π:素元, O:整数環, q：剰余体の位数, m:極大イデアル ・F=F(X,Y)∈O[[X,Y]]が形式群とは次を満たすことである： ・F(X,Y) = X+Y+(2次以上の項) ・F(X,F(Y,Z)) = F(F(X,Y),Z) ・F(X,i(X)) = 0 となる i(X)が存在する ・F(X,Y)=F(Y,X) ・Fが形式群のとき、x,y∈m に対して、F(x,y)∈mが定まる。 このようにして、m_kに（通常と別の）群構造を入れることができる。 * F(X,Y)=X+Y のとき、上記は通常の群構造と同じ * F(X,Y)=X+Y+XY のとき 1+mの乗法群の群構造に対応 * 楕円曲線の加法を(x座標について)冪級数展開したものをFとすると楕円曲線の加法に対応 ・F,Gを形式群とする。h∈TA[[T]]が準同型:F→Gであるとは： h( F(X,Y) ) = G( h(X),h(Y) ) を要求する。 （互いに逆写像となる準同型がある時、2つの形式群は同型である。） h1,h2が準同型のとき、その加法を G(h1,h2) で定めると、 準同型F→Gの集合は、アーベル群をなす。 さらにF=Gの場合は、乗法を、合成h2(h1(・)) で定めると、 準同型F→Fの集合は、（可換とは限らない）環をなす。 ・「Lubin-Tate形式群」 f(X) ≡ πX + (2次以上の項) かつ f(X) ≡ X^q (mod π) という形のべき級数を考える （原点での微分がπであり、mod π還元でフロベニウス写像となる） 例えば f1(X) = πX+X^q f2(X) = (1+X)^p-1 [K=Q_p,π=pの場合] [命題] このようなfに対して、fを自己準同型に持つ形式群Fが一意的に定まる （このような形式群を「Lubin-Tate形式群」と呼ぶ） Lubin-Tate形式群は、実は(fに依らず)、すべて同型となる（すごい事実） * f( F(X,Y) ) = F( f(x),f(y) ) を満たすということ * 上記のf2に対しては、F2(X,Y)=X+Y+XY が対応する f1に対して、π=q=3の場合で計算機で係数比較で逐次求めてみると F(x,y)=x+y+xy(x+y)/8-xy(x^3+y^3)/128 +xy(x^5+y^5)/2^10-5xy(x^7+y^7)/2^15+... という具合であった。良く分からないけど確かに一意的に決まりそうではあった。 ・a∈Oに対して「a倍写像」 F→F を定めたい [a](T) = aT + (2次以上の項) かつ f([a]) = [a](f) を満たす冪級数[a](T)∈O[[T]] が一意的に存在し、準同型F→Fを与える。 上記のf2,F2に対して [a]=(1+T)^a-1 である。 なお、定義から[π] = fである。 ---------- Kの代数閉包K^alを考える。 Λ = {α∈K^al | |α|<1 }に Λの元α,βに対してF(α,β)で二項演算を定め、[a](α)で[a]倍写像を定める。 [π]^n 倍して0になるような元をΛ[n]とおく。 （定義から[π]^n 倍とはfをn回作用させるという意味である） Λ[n]はq^n個の元を持つことが分かる。 （これがQ_pのときの1の原始p^n乗根の役割をする。） [定理]（かなりすごい事実） K[Λ[n]]/K はφ(q^n)次のtotallyな分岐拡大であり、 上記に定めた [a]倍写像は、K[Λ[n]]の体の自己準同型を与え、 aを単元に制限すれば体の自己同型を与え、ガロア群をなす。 ・局所アルティン写像 θ(a)のK_πとK^unrへの作用をそれぞれ記述すれば良い。 a = u*π^m [uは単元]とおく。 K_πには、 [u^-1]倍写像として作用し、 K^unrには、フロベニウス写像(p乗)のm回合成として作用する。 uに-1乗をつけたことによって、結果はπの選択に依存しない。
22:13 2019/02/23