Γをフルモジュラー群とする。 Γはよく知られているように上半平面Hに作用する。((az+b)/(cz+d)のように) j関数: H→C があって、z1,z2∈Hに対して j(z1)=j(z2) ⇔ γ∈Γがあってγ(z1)=z2 つまりこのときj関数は Y=H/Γ上の関数と考えることができて、 これにより、Y→Cは正則同型と言える。（たぶん） Hにcuspを追加したものをH*とする。 cuspとは∞と、実軸上の有理数である。（これらは、Γの元で移りあう） X=H*/Γは、Yにcuspを1つ追加したものである。 これにより、Xはリーマン球面に正則同型となる。 ・被覆の考察で扱ったΓ(2)を考える。 これは [[A,B],[C,D]]≡[[1,0],[0,1]] (mod 2) という合同部分群を意味している。 Y2 = H/Γ(2) X2 = H*/Γ(2) とおく。λ関数は、正則同型 Y2 → C-{0,1} を引き起こすのだった。 基本領域には3つのcusp{0,1,∞}があって、これらはΓ(2)の元で移りあわない。 X2は、Y2に3点追加したもので、X2もリーマン球面に正則同型であろう。（たぶん） ・Γ(2)の基本領域は、Γの基本領域を6つ合わせたものだった。 そこで、6重の分岐被覆 X2→X, Y2→Xがある。 これについて、リーマンフルヴィッツの公式を観察することをした。 ・分岐点の観察： iの逆像は3点（×印、2重点×3）1+1+1 = 3 ωの逆像は2点 (〇印、3重点×2) 2+2 = 4 ∞の逆像は3点 ({0,1,∞}、2重点×3) 1+1+1 = 3
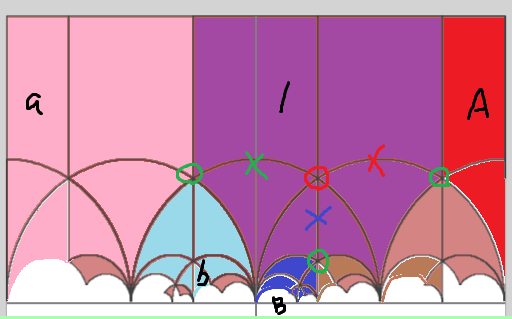リーマンフルヴィッツの公式に当てはめると、
χ(Y2) = 6*χ(Y)-3-4-3
χ(X2) = 6*χ(X)-3-4
となるはずである。
コンパクト、つまり閉リーマン面のオイラー標数は、2-2gで良いが、開リーマン面の場合はどうだろう。
実多様体としての特異ホモロジーH^0,H^1,H^2の次元の交代和に戻って考える。
（閉リーマン面の場合は 1,2g,1 であった）
（H^1の次元は基本群の生成元の個数と認識している。）
Cからn点取り除いた開リーマン面ではこれらの次元は、1,n,0になると思う。
従ってオイラー標数は1-nとなる。
https://math.stackexchange.com/questions/1244681/difference-between-euler-characteristics-of-a-riemann-surfaces
実際に種数gの閉リーマン面からr点除いたもののオイラー標数は2-2g-rらしい。
Cからn点取り除いたものは、リーマン球面から(1+n)点取り除いたものと解釈すると合致する。
なので、オイラー標数は
χ(Y2)=2, χ(Y)=2,
χ(X2)=-1, χ(X)=1
となる。これを上記の等式に当てはめると、成立が観察できる：
2 = 6*2-3-4-3
-1 = 6*1-3-4