＝＝
  [3] 円分多項式の場合

[命題3-1]
Φ_k(x)をk次円分多項式とする。pをkと互いに素な素数と仮定する。
Φ_k(a)がpで割り切れるとき、aは「pを法として1の原始k乗根」である。
これはa^n≡1(mod p) を満たす最小の正整数nがkであるという意味である。

[命題3-1の説明]
k=15を例にして仕組みを説明する。円分多項式の性質によって、
x^15-1=Φ_1(x)Φ_3(x)Φ_5(x)Φ_15(x) のように分解されることに注目する。
これよりΦ_15(a)がpで割り切れる時、a^15≡1 (mod p)である。
a^n≡1 (mod p)を満たす最小の正整数が15である確認が課題である。

a^n≡1 (mod p)を満たす最小の正整数の候補は15の約数に限るから以下に帰着する：
Φ_15(a)がpの倍数ならばΦ_1(x),Φ_3(x),Φ_5(x)はpの倍数ではない。
pとkが互いに素という仮定と、指数持ち上げの補題を使って示すことができる。
例えばΦ_3(x)とΦ_15(x)がともにpの倍数であると仮定すると、
x^15-1がpで割り切れる回数はx^3-1がpで割り切れる回数より多いはずである。
ところが指数持ち上げの補題を適用すると以下の関係がある。
(x^15-1がpで割り切れる回数) = (x^3-1がpで割り切れる回数) + (5がpで割り切れる回数)
先の指摘と合わせるにはp=5とするしかないがpとkが互いに素という設定に反する。

---
[命題3-2]
素数pを法とするとき、pと素な(p-1)種類の剰余類は、1の(p-1)乗根の構造を持つ。よって
「pを法として1の原始k乗根」が(整数範囲で)存在する ⇔ kは(p-1)の約数である

言い換えると「原始根定理」である。tsujimotterさんの記事もある。
スクリプトd1(上)が観察に役に立つと思う。

[命題3-2の説明]
p=7を例に仕組みを述べておく。フェルマーの小定理を既知とする。
x^(p-1)-1 ≡ (x-1)(x-2)...(x-(p-1)) (mod p) という分解が存在する。
これは合同式における因数定理から従う。

円分多項式による分解 x^6-1 = Φ_1(x)Φ_2(x)Φ_3(x)Φ_6(x) と比較する。
先の分解のいくつかの因子はΦ_6(x)の因子となるはずである。
[命題3-1]より、その因子を0とするxは「pを法とする原始7乗根」である。

---
[命題3-3]
素数pを法とするとき、pと互いに素な(p^2-1)種類の「2次の無理数」の剰余類は、
1の(p^2-1)乗根の構造を持つ。よって
「pを法として1の原始k乗根」が「2次の無理数」までの範囲で存在する ⇔ kは(p^2-1)の約数

[命題3-3の説明]
冒頭で少し紹介した「2次の無理数」を改めて説明する。
p=2ではこの構成は使えないのでpは奇素数とする。
pを法とする非平方剰余q (x^2≡q (mod p)が整数解を持たないようなq) を1つとる。
集合{A+B√q|A,B∈Z}を2次の無理数と呼ぶ。
A+B√q≡C+D√q (mod p) ⇔ A≡C,B≡D (mod p) と定める。
従って、A,Bそれぞれp種類でp^2個の元がある。

# 例えばp=7では {[A+B√3] | A,Bは0から6までの整数} で49種類を代表できる。
演算は自然に計算される通りに定義される。
例えば(3+√3)(5+√3)=18+8√3≡4+√3 (mod 7)

この「2次の無理数」たちにもいくつかの自明でない重要な性質が成り立つ。
・「xy≡0 ⇒ x≡0またはy≡0」が成り立つ。（qが非平方剰余であるという設定のおかげ）
・「フェルマーの小定理」 x≡/0 (mod p) ⇒  x^(p^2-1)≡1 (mod p) が成り立つ。
これは群論のラグランジュの定理から従う。tsujimotterさんの記事を紹介する。
・そうすれば「原始根の存在」（命題3そのもの）は[命題2]と同様に証明できる。
p=7の場合はx^48-1の円分多項式による分解を考えれば良い。

スクリプトd1(下)が観察に役に立つと思う。この使い方を説明しよう。
デフォルトで入力されている値で表を作成すると下記のような表が出力される。

これは、A+B√q=2+√3を冪乗した時にN=7で割った余りの挙動を示している。
例えば横列a=5, 縦列b=6のところに5と書いてあることは、
(2+√3)^5≡a+b√q=5+6√3 (mod 7)であることを意味する。
(2+√3)^8≡1 (mod 7)であるから、(2+√3)^kは最短周期8を持つことが分かる。
A,Bを適当に変更して作成ボタンを押すと、表を埋め尽くすものを見つけることができる。
例えばA=2, B=3 とすると (2+3√3)^k は48種類を網羅する。（原始根である。）

---
[命題3-1の再掲]
Φ_k(x)をk次円分多項式してpをkと互いに素な素数とする。
Φ_k(a)≡0 (mod p)のとき、aは「pを法として1の原始k乗根」である。

ここに登場するaは整数の代わりに「2次の無理数」でも良いことを指摘しておく。
（議論は同様である）

---
[本題3-1]
k次円分多項式Φ(x)が素数pで割り切れる整数xが存在する条件を考える。
命題1を適用するためにpはkと互いに素な素数に限って議論する。

[命題3-1]よりpを法として1の原始7乗根が存在するかどうかと同値である。
[命題3-2]よりkが(p-1)の約数であることと同値である。
すなわち p=kZ+1型素数であることと同値である。
このようにして、円分多項式そのものの素因数集合は説明がついた。

[本題3-2]
Φ(x)が素数pで割り切れる2次の無理数範囲のxが存在する条件を考えると
[命題3-1の再掲]と[命題3]よりkがp^2-1の約数であることと同値である。

# ここで具体的にk=7としてΦ(a)≡0 (mod p) となるaを具体的に求めてみよう。
# p=29
スクリプトd1(上)でN=29として表を作成する。
x=2の行が28種類を網羅しているので、x^(28/7)=x^4=16 をとれば原始7乗根である。
さらに改めてx=16の行をみれば、他の原始7乗根たちもすべて抽出できる。
Φ(x)≡(x-16)(x-24)(x-7)(x-25)(x-23)(x-20) (mod 29)　を得る。

# p=13
スクリプトd1(下)でN=13で表を作成する。
A,B,qを適当に変えながら探すとA,B,q=2,1,2で(A+B√q)^kは168種類を網羅する。
原始7乗根を得るにはそのA,B,qで(A+B√q)^(168/7)をとれば良い。
スクリプトにちょうど良い機能をつけてある。
表の下にある「k=＿」の空欄に168/7と入力して値ボタンを押せば4+√2を得る。
Φ(4+√2)を実際計算機に計算させると 15691+10751√2 = 13*(1207+827√2) である。
また、改めてA,B,q=4,1,2と入力すれば、Φ(a)=[0]となる6種類のaを抽出できて次を得る。
Φ(x)≡(x-4+√2)(x-4-√2)(x-10+2√2)(x-10-2√2)(x-5+5√2)(x-5-5√2) (mod 13)

＝＝
   [4] それ以外の場合　前編

最小多項式の行き来と合同式を関係づける命題を先に準備する。

[命題4-1]
αが最小多項式がΦ(x)で、β=g(α)の最小多項式がf(x)である状況を考える。
g(x)は整数係数多項式とする。pを任意の素数とする。
Φ(a)≡0 (mod p) ならば b=g(a)とおけば f(b)≡0 (mod p) も成り立つ。

[命題4-1の説明]
αの最小多項式の性質としてF(x)=0がx=αを解に持つならF(x)はΦ(x)を因数にもつ。
今回の設定ではF(x)=f(g(x))で適用できて、よって f(g(x)) = Φ(x)*(商多項式) と書ける。
この式でx=aを代入すれば結論を得る。

---
[命題4-2]
αの最小多項式をΦ(x)、βの最小多項式をf(x)、
係数にβを含む範囲でのαの最小多項式をF(x,β) とする。
pをF(x,β)の分母に現れる数（有れば）と互いに素な素数とする。
f(b)≡0 (mod p) ならば F(a,b)≡0 (mod p)を満たすaをとれば f(a)≡0 (mod p) も成り立つ。
特に、bが整数で、F(x,β)がxの2次式ならば、aは「2次の無理数」範囲で存在する。

[命題4-2の説明]
αの最小多項式の性質よりΦ(x)はF(x,β)*(商多項式1)と書ける。
次にβの最小多項式の性質よりΦ(x)-F(x,y)*(商多項式1)=f(y)*(商多項式2)と書ける。
これにy=bを代入すれば結論を得る。後半は以下の補題による。

[補題]
[3]の方法で2次の無理数範囲を構成する。
pを法とする任意の2次方程式はその範囲に解を持つ。
（有限体の言葉では、有限体の一意性という内容である）

[補題の説明]
平方完成すれば(x-s)^2≡t (mod p)と変形できる。tが平方剰余なら整数範囲に解を持つ。
tが平方非剰余なら2次の無理数の構成に使った平方非剰余qを使って
t=qu^2となるuがとることができてx=s±u√qが解となる。

---
[本題4-1]
1の原始7乗根αの最小多項式はΦ(x)=x^6+x^5+x^4+x^3+x^2+x+1であり、
β=α+α^6の最小多項式はf(x)=x^3+x^2-2x-1である。
f(x)の素因数が7の他には7Z+1,6型素数に限ることを説明する。
F(x,β)=(x-α)(x-α^6)=x^2-βx+1 を使って[命題4-2]を適用できる。

[命題4-2]はやや複雑なので中身を追いつつ適用してみる。
商多項式1,2を具体的に書き下してみると以下のようになる。
Φ(x)-F(x,y)*(x^2+(y^2+y-1)x+1)(x^2-(y^2-2)x+1) = f(y)*(yx^2-xy^2+x+y)x^2

f(b)≡0 (mod p) を満たす整数bが存在するなら、
[補題]によってF(a,b)≡0 (mod p)を満たすaを2次の無理数範囲でとれて、
それらを上記の式に代入すると
Φ(a) = f(b)*(ba^2-ab^2+a+b)a^2 の関係を得る。よってf(b)≡0 から Φ(a)≡0 が従う。
あとは[本題3-2]から、kがp^2-1の約数であることが条件となる。
すなわちpは7Z+1,6型素数に限ることが言えた。

[本題4-2]
1の原始15乗根αの最小多項式はΦ(x)=x^8-x^7+x^5-x^4+x^3-x+1であり、
β=α+α^4 の最小多項式は f(x)=x^4-x^3+2x^2+x+1である。
f(x)の素因数が2と15Z+1,4型素数に限ることを説明する。
同じように[命題4-2]を適用していくと、2つの問題が新しく発生する。

問題1：
αのQ(β)係数最小多項式がβの多項式としては整数係数ではない。
F(x,β)=(x-α)(x-α^4)=x^2-βx-β^3/2+β^2-β-1/2
それに伴い、商多項式1,2も整数係数ではなくなる。

実際に商多項式の式を一部省略しつつ具体的に書き下すと
Φ(x) - F(x,y) *(x^2+(-y^3+y^2-2y-1)x+(y^3/2-y^2+y-1/2))
 *(x^2+(y^3/2-y^2+2y-1/2)*x+(-y^3/2+y^2-y-1/2))
 *(x^2+(y^3/2+y+1/2)*x+(y^3/2-y^2+y-1/2))
 = f(y)*(長い整数係数多項式)/16 という関係である。

f(b)≡0から F(a,b)≡0となるaを2次の無理数範囲でとる所までは良いが、
Φ(a)=f(b)*(長い整数係数多項式)/16 という関係式を得た時に
f(b)がpの倍数でもそれが分母で打ち消されればΦ(a)がpの倍数とは言えない。

p=2が該当し、実際 f(x)≡0 (mod 2) となる整数xは存在するが
Φ(x)≡(x^4+x^3+1)(x^4+x+1) (mod 2) であり右辺の因子はmod 2で既約だから
Φ(x)≡0 (mod 2)となるxは4次の無理数まで範囲を広げないと存在しない。

しかし分母に現れる素因数は有限個だから問題1は有限個を除けば解決する。
よってそれらを除くことで、
Φ(a)≡0 (mod p)となるaが2次の無理数範囲で存在すると議論を続ける。
さらに[命題3-1]を適用するためにp=3,5も予め除いて議論を続ける。

問題2：
[本題3-2]を適用してkがp^2-1の約数である所までは言えるが、
kが合成数であるため、p=15Z+1,4,11,14型という具合に4系統存在する。
そこから15Z+1,4型に絞るにはもう一歩必要である。

＝＝
  [5] それ以外の場合　後編


例のスクリプトを使って、Φ(a)≡0 (mod p)となる2次の無理数を実際に求めてみる。
p≡1,4,11,14 (mod 15)に対応して、p=31,19,11,29を例にする。
p=31では有理整数範囲で存在してa=7
p=19では a=1+4√2, p=11では a=1+2√2, p=29では a=2+4√2 を得る





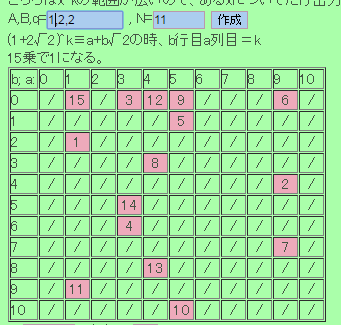
この表から発見がある。
p=19では(1+4√2)^4 が 1+4√2の共役
p=11では(1+2√2)^11 が 1+4√2の共役
p=29では(2+4√2)^14 が 2+4√2の共役
共役を得る指数は、ちょうどpを15で割った余りと一致している！
この巧妙な仕組みが「フロベニウス写像」と呼ばれることを後で知った。

すなわち
「フロベニウス写像」f(x)=x^p は「共役」を与える。

[説明]
・例えばα=1+4√2 の有理数係数最小多項式は x^2-2x-31である
多項定理により (x^2-2x-31)^p ≡ (x^p)^2-2(x^p)-31 (mod p) であるから
β=α^p はpを法としてαと同じ最小多項式を持つ。
従ってβは1±4√2のどちらかに合同である。
全く一般的に同様にx=A+B√qに対してx^pはA±B√qのどちらかに合同と言える。

一方、原始根の存在の証明でも登場したような分解：
x^p-x ≡ x(x-1)(x-2)...(x-(p-1)) (mod p) が存在する。
x=A+B√qをこの分解に代入すると、
[3]でちらっと紹介したように「xy≡0⇒x≡0またはy≡0」が成り立つので
B≡/0 (mod p)ならば右辺≡/0であり、すなわちx^p≡/xである。
従ってx^pはxとは異なる方のA-B√qであるはずだ。

---
[本題4-2の続き]

aは F(x,b)=x^2-bx-b^3/2+b^2-b-1/2 の解であった。
F(x,β)=(x-α)(x-α^4)という構成によって、
1つの解をaとするとa^4がもう1つの解となるはずである。

aが有理整数である場合と、真に2次の無理数である場合に場合分けする。

・aが有理整数の場合はΦ(a)=[0]となる整数aが存在するわけだから、
[本題3-1]よりpは15Z+1型素数と要求される。

・aが真に2次の無理数である場合は、a^4がaの「共役」ということになる。
フロベニウス写像によるとa^pもaの共役である。
また、[命題3-1]によりaは1の原始15乗根である。
これらを合わせれば、p≡4 (mod 15)が要求される。

αとα^4が共役である関係とpが15N+1,4型素数という条件を、
フロベニウス写像が巧妙に結びつけている！

ところでf(b)≡0に対して a=(b±√(2b^3-3b^2+4b+2))/2 がΦ(a)≡0を満たすことから
上の場合分けは√の中身がpを法として平方剰余かどうかと同値となる。
従って次の予期しない副産物を得る：
b^4-b^3+2b^2+b+1が素数pの倍数のとき：
pが15Z+1型のとき2b^3-3b^2+4b+2 はpを法として平方剰余である
pが15Z+4型のとき2b^3-3b^2+4b+2 はpを法として平方剰余でない

---
[本題5]
フロベニウス写像を使うと「逆」を確認することができる。
つまりpが7Z+1,6型素数のときに
f(x)=x^3+x^2-2x-1がpで割り切れる整数xが実際に存在することを説明する。

(1) pが7Z+1型素数のときはΦ(a)=0となる整数aが存在する。
[命題4-1]によりb=a+a^6とすればf(a+a^6)=[0]となる。

# p=29に対して[3]で求めたa=16から、b=16+16^6≡7 (mod 29) を得る。
実際f(7)=377は29で割り切れる。

(2) pが7Z+6型素数のときは、Φ(a)=[0]となるaが真の2次の無理数として存在する
b=a+a^6とすればf(a+a^6)≡0であるが、このbが整数としてとれることを言う必要がある。
[命題3-1の再掲]を思い出す：a^7≡1 (mod p) 
さらにフロベニウス写像を持ちだす：a^pはaの共役
pが7Z+6型素数であるという設定と合わせると、a^6はaの共役であることが言える。
よってa+a^6は有理数(に合同)であることが言える。

# p=13に対して[3]で求めたa=4+√2からb=(4+√2)+(4-√2)^6≡8 (mod 13)と得て
実際f(8)=559は13で割り切れる。

k=15の場合でもこの方向は支障なく同様に議論できる。

＝＝
  [6] 割り切れる回数


（例外を除いて）好きな回数だけ割り切れるxが存在することを説明する。
指数持ち上げの補題「x≡1 (mod p^n) ⇒ x^p≡1 (mod p^(n+1))」が有用である。
Φ(a)≡0 (mod p^n) ⇒ Φ(a^p)≡0 (mod p^(n+1))が成り立つわけである。
これにより目的のxを具体的に得ることができる。

# p=29として Φ(a)≡0 (mod 29^n)となるaを求めてみる。
n=1に対して[3]で得たa=16を採用できる。
16^29≡190 (mod 29^2) = 16+6*29
190^29≡1872 (mod 29^3) = 190+2*29^2
...
x=1872をとればΦ(x)が29^3で割り切れる。

[2]でちらっと触れた局所体への還元という視点からは、
「Φ(a)=0 となるaが29進数として存在する」と記述できる。
上記の結果は29進展開的に a = 16+6*29+2*29^2+... と書けるのである。

# f(x)=x^3+x^2-2x-1に対してf(b)≡0 (mod 13^n)となるbを求めてみる。
Φ(a)≡0 (mod 13^n)となる2次の無理数aを使う。
n=1に対して[3]で得た a≡4+√2 (mod 13)を利用する。
(4+√2)^13 ≡ 17+12√2 (mod 13^2)
(17+12√2)^13 ≡ 1876+1509√2 (mod 13^3)
...
b=a+(aの共役)、つまりaの有理部分の2倍をbとすればf(b)≡0 (mod 13^n)となる。
実際x=2*1876をとればf(x)が13^3で割り切れる。

局所体の不分岐拡大という視点からはこの状況は
「Φ(a)=0となるaがQ_pの2次不分岐拡大Q_p^2に存在する」と記述される

・一方で、割り切れる回数に限りがある例外的な素数pを挙げるのに
局所体の理論である「ヘンゼルの補題」を使うと次の結果を得られる：
そのような素数pは、f(x)の「判別式」の素因数に限る

[説明]
ヘンゼルの補題が主張することには、
f(a)≡0 (mod p) となるaが存在し f'(a)≡/0 (mod p)であれば、
f(a)=0 となるaがp進数として存在する。
言い換えると任意のnに対して f(a)≡0 (mod p^n)となるaが存在する。

例外的な素数は、f(a)≡0 となるaがf'(a)≡0 を同時に満たしてしまう場合である。
f(x)の判別式が0であることは、f(x)とf'(x)が共通因子を持つかどうかと同値である。
そこで、類推的なのだが、f(x)の判別式がpの倍数であることは、
f(a)とf'(a)は(mod p)で共通因子を持つことと同値である。
そういうわけで例外的な素数はf(x)の判別式の素因数となっているはずである。

これにより[本題4-2]で取り挙げた例のp=2も実際に拾うことができる。
MaximaやWolfram Alphaにpoly_discriminant(x^4-x^3+2*x^2+x+1,x) と尋ねれば
900と答える。素因数p=2,3,5が、割り切れる回数に限りがある素数の候補である。