＝＝
  [7] 素イデアル分解との関係


素イデアル分解の概念に関してはtsujimotterさんが既に記事を書いている。
ここでは今まで述べた現象との関係を紹介するのが目的である。

f(x)がpで割り切れるようなxがm次の無理数に存在することは、
f(x)が(mod p)でm次式に因数分解できると言い換えられる。
そして、f(x)の(mod p)での分解は、イデアル(p)がf(x)による最小分解体においてどう分解するかと密接に関係する。（説明はできない。観察のみである。）

Φ(x)=x^2+1については
p=5のような4Z+1型素数ではΦ(x)≡(x+2)(x-2) (mod 5)と分解できて、
素イデアル(5)も(i+2)(i-2)と分解する。
p=3のような4Z+3型素数ではΦ(x)は既約で、イデアル(3)も分解できない。

1の原始7乗根αとΦ(x)=x^6+x^5+x^4+x^3+x^2+x+1について
7Z+1型素数　p=29 では
Φ(x)≡(x-16)(x-24)(x-7)(x-25)(x-23)(x-20) (mod p) と6個に分解し、
イデアルも (29)=(α^2+2α+2)(α^4+2α^2+2)(α^6+2α^3+2)(2α^4+α+2)(2α^5+α^3+2)(2
^6+α^5+2) と6個に分解する。

より関係が分かりやすい記述をすると：
(29)=(α-16,29)(α-24,29)(α-7,29)(α-25,29)(α-23,29)(α-20,29)である。
(α-16,29)は{(α-7)x+29y|x,y∈Z[α]}というイデアルを意味している。
(α^2+2α+2)はこれを単項イデアルで表現したものである。
実際、例えば (α^2+2α+2)=(α-16)X+29Y を満たすX,Y∈Z[α]が存在する。
これを計算機を駆使して求めるような課題はやりがいがあるので横道にそれるが紹介する。
---
α^2+2α+2の共役たち(α^4+2α^2+2)(α^6+2α^3+2)(2α^4+α+2)(2α^5+α^3+2)(2α^6+α^5+2)
を上の式の両辺に掛けると両辺が29でくくれるはずである。整理して：
29=-29(3α^5-α^4+α^3+5α^2-7α+9)X+29(5α^5-2α^4+2α^3+8α^2-12α+16)Y
両辺を29で割り -(3α^5-α^4+α^3+5α^2-7α+9)X≡1 (mod 29) として考える。
F_29^6の視点から、(3α^5-α^4+α^3+5α^2-7α+9)^(29^6-1)≡1 のはずだから
X≡-(3α^5-α^4+α^3+5α^2-7α+9)^(29^6-2)をとるのが１つの方法である。
実行してX=-(5α^5+27α^4+2α^3+8α^2+16α+27)を得る。元の式に代入して、
α^2+2α+2=-(α-16)(5α^5+27α^4+2α^3+8α^2+16α+27)
 -29(2α^5+15α^4+α^3+4α^2+8α+15) と目的の関係式を得る。
---
7Z+6型素数　p=13 では
Φ(x)≡(x^2+3x+1)(x^2+5x+1)(x^2+6x+1) (mod 13)　と3つの積に分解し
対応してイデアルも (13)=(α^6+α+3)(α^5+α^2+3)(α^4+α^3+3) と3つに分解する

Φ(x)の分解を得る1つの方法には[3]の最後で得た分解で共役同士を掛ければ良い：
Φ(x)≡(x-4+√2)(x-4-√2)(x-10+2√2)(x-10-2√2)(x-5+5√2)(x-5-5√2) (mod 13)

素イデアルの分解をガロア群と結び付けて記述する言葉が「分解群」である。

# k=7,p=13の場合を例に「分解群」を考えてみる。
代数拡大L/QとしてQ(α)/Qで考えている。
Qの素イデアル(7)が、Lにおいては3つの素イデアル(p1)(p2)(p3)に分解する状況である。
Q(α)/Qのガロア群をZ/7Z*={1+7Z,2+7Z,3+7Z,4+7Z,5+7Z,6+7Z}と同一視する。
αをy乗する写像を y+7Z という剰余類と同一視しているわけである。
そのガロア群の元は素イデアルに作用して(α^6+α+3)を((α^y)^6+α^y+3)に置換する。
その作用で 1+7Z,6+7Z は素イデアルp1,p2,p3を固定し、残りはこれらを巡回置換する。
「分解群」は素イデアルを固定する元の集合と定義され、この場合{1+7Z,6+7Z}である。

今の場合は不分岐だから惰性群は自明な{1}で、
分解群がそのまま剰余体の代数拡大のガロア群と対応する、
という視点がヒルベルトの分岐理論である。
そこで剰余体＝有限体の代数拡大のガロア群は、フロベニウス写像で生成される。
それに対応して、分解群はp乗写像である p+kZ で生成されるわけである。

# k=15の場合にそれは顕著である。
p=2: Φ(x)=x^8-x^7+x^5-x^4+x^3-x+1≡(x^4+x+1)(x^4+x^3+1),
 (2)=(α^4+α+1)(α^14+α^11+1)
p=19: Φ(x)≡(x^2-2x+7)(x^2-6x+7)(x^2-3x-8)(x^2-9x-8)
 (19)=(α^4+α-2)(α^8+α^2-2)(α^14+α^11-2)(α^13+α^7-2)
p=29: Φ(x)≡(x^2-4x+1)(x^2-14x+1)(x^2-20x+1)(x^2-21x+1)
 (29)=(5α^13+5α^2-3α^14-3α-15)*(その共役たち)

p=2の分解群は{1+15Z,2+15Z,4+15Z,8+15Z} (2+15Zで生成されている)
※(α^8+α^2-1)=(α^4+α-1)(α^5+1),(α^4+α-1)=(α^8+α^2-1)(-α^5)
という関係で(α^8+α^2-1)と(α^4+α-1)はイデアルとして等しい。
p=19の分解群は{1+15Z,4+15Z} (19+15Z=4+15)
p=29の分解群は{1+15Z,14+15Z} (29+15Z=14+15Zで生成されている)
という具合である。

・f(x)の分解とイデアル(p)の分解が綺麗に対応しない例を発見した。
f(x)=x^4-x^3+2*x^2+x+1≡(x+1)^2*(x^2+x+1) (mod 2)
イデアルの分解は (2)=(β+1)*(β^2+β+1)
[本題4-2]でも問題を起こした曲者である。

（おそらくQ(β)の整数環がZ[β]でないことが関係している。
代数体の情報を得るにはlmfdbがおすすめで
Field欄にx^4-x^3+2x^2+x+1と入力して至るページで
整数環の基底が[1, β, β^2, β^3/2-1/2] と分かる。）

[2021/10/31 追記]
p進数係数で分解すれば、正しく対応する。
mod pでは(x+1)^2に分解される2次式が、p進数係数では既約なのである。
（そのようなことが起き得るのを納得するには例えばx^2-pを考えれば良い。）


＝＝
  [8] Qの類体論


[1]で提示した結果[命題1]を再掲する：
「αを1の原始k乗根とする。αの最小多項式はオイラーのφ関数によってφ(k)次である。
m個の元からなる集合Aをうまくとって、
β=Σα^d [d∈A] の共役がちょうどm個ずつ重複するようにする。
βの最小多項式f(x)はφ(k)/m次になるはずである。
f(x)の素因数の集合は有限個の例外を除いてkZ+d型素数(d∈A)全体である。」

この記述では、k=12, A={1,7}のような場合にβ=0となってf(x)が構成できない。
代数的整数論の言葉を使うとより普遍的に記述することができる。

[命題1の改良]
Lをk次円分体とする。
円分拡大L/Qのガロア群GはZ/kZの既約剰余類がなす乗法群と同一視される。
Gの部分群Aに（ガロアの基本定理の意味で）対応する中間体をMとする。
このとき
・f(x)の最小分解体がMとなるような多項式f(x)の素因数の集合は、
有限個の例外を除いてkZ+d型素数(d∈A)全体である。
より本質的には
・Qの素イデアル(p)をMに延長したときにpが完全分解する⇔p≡d (mod k), d∈A

このような状況の時、実は、Mは「類体」なのである。
補足すると、「Q上の、（Aに対応する）ある「合同群」による、類体」である。

---
本話題に出会った一番最初のきっかけは、私的数学塾というウェブサイトで
「私の備忘録」の「S(H)さんからの話題」で見かけた次のような記述であった：
「X^4+52X^3-26X^2-12X+1=0の解の1つをζとすると
他の解は-4ζ/(1-ζ)^2,(1-ζ)/(1+3ζ),(1-ζ)(1+3ζ)/(-4ζ^2)で表せる」

そのように解の1つを使って残りの解を表せるような多項式について調べていると、
整数を代入した時の素因数の集合があるkを法とする分布を示すことに気づいたのだ。
それは偶然ではなく、実際次は同値である：
・f(x)=0の解の1つを使って残りの解を表せる
・f(x)=0の解をある1の原始k乗根を使って表すことができる
・f(x)に整数を代入した時の素因数の集合があるkを法とする分布となる

最初の条件は、f(x)の最小分解体がQ上のアーベル拡大であることを示している。
次の同値は、Qのアーベル拡大とはすなわち円分拡大であるという主張による。
これはクロネッカーウェーバーの定理と呼ばれるものである。
最後の同値は「類体とはすなわちアーベル拡大なり」として知られる。

2018/2/13 追記。間違いが判明した。
f(x)=0の解の1つを使って残りの解を表せるが、
f(x)の最小分解体がQ上のアーベル拡大でない例が存在することが確認できた。
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q10186000275
2018/3/1 追記。上記リンク先で
「今回の状況では任意の中間体K⊂M⊂Lに対して、M/Kもガロア拡大である」
とか書いてますが、それも勘違いで、全然そんなことなかった。
＝＝
  [9] Q(i)の類体論


類体論が主張することには、基礎体KがQ以外の場合にも、
Kのイデアルを「合同群」によって分類したときに、
対応する法則で素イデアルが完全分解するような拡大体M/Kが存在する。

特にKが虚二次体の場合には楕円曲線や虚数乗法論が関係する。
特にK=Q(i)の場合に関係するのはレムニスケート関数でもある。
今回、Q(i)の類体の挙動を実際に観察してみたのを紹介したい。

[8]に現れた多項式X^4+52X^3-26X^2-12X+1は実はレムニスケート関数に由来した。
この関数についてはネットで検索して出会った下記資料で詳しく知った：
http://www.juen.ac.jp/math/nakagawa/ellfunc.pdf

この段落は上記の資料を参考にして書いている。
u=∫[0..r] 1/sqrt(1-t^4) dt の逆関数として r=sn(u)と定義する。
この関数でも加法定理やn倍角の式のようなものを計算できる。(「角」ではないけど・・)
sn(a+b)={sn(a)sn'(b)+sn'(a)sn(b)} / {1+sn(a)^2sn(b)^2}
sn(a+b*i)={sn(a)sn'(b)+i*sn'(a)sn(b)} / {1-sn(a)^2sn(b)^2}
ただし sn'(u) = sqrt(1-sn(u)^4)
sn(u)=s と略記する。
sn(2u) = 2s* sqrt(1-s^4) / (s^4+1)
sn(3u) = s* (s^8+6s^4-3) / (3s^8-6s^4-1)
sn(4u) = 4s* sqrt(1-s^4)* (s^4+1)* (s^8-6s^4+1) / (s^16+20s^12-26s^8+20s^4+1)
sn(5u) = s* (s^8-2s^4+5)* (s^16+52s^12-26s^8-12s^4+1)
 / (5s^8-2s^4+1)* (s^16-12s^12-26s^8+52s^4+1)

5倍角の式の分子に、先のf(x)がf(s^4)として現れている。

・ガウス整数範囲での素因数集合を考えると、
やはり今まで紹介したQの類体と同様のことが起こることが観察できる。
実際f(x)=x^4+52x^3-26x^2-12x+1 をガウス整数環の範囲で素元分解すると、
素因子は5を除いて{p|p≡±1,±i(mod 5)}と分布する。

・そこで今回、新しく、(1+4i)倍角の式を計算機を使って計算してみた。
sn((1+4i)u) = {sn(u)sn'(4u)+i*sn'(u)sn(4u)}/{1-sn(u)^2*sn(4u)^2}
sn'(4u)=sqrt(1-sn(4u)^4) において根号の中身を因数分解すると有理式の平方となる。
その根号をとるときは、s=0を代入した時に1になるほうの符号を選択した。
展開すると sn((1+4i)u) = s*(sの32次式)/(sの32次式)　という結果になった。
s^4=x とおくと s*(xの8次式)/(xの8次式) となり、
分母と分子はQ(i)係数の4次式を共通因数として約分できることが判明し、その結果
sn((1+4i)u)=s*{x^4+(12-20i)x^3+(-10+28i)x^2+(-20-12i)x+(1+4i)}
/ {(1+4i)x^4+(-20-12i)x^3+(-10+28i)x^2+(-12-20i)x+1} を得た。

この分子f(x)=x^4+(12-20i)x^3+(-10+28i)x^2+(-20-12i)x+(1+4i)の素因数を観察する。
いくつかのf(x)の値と分解を挙げる。
（2の冪の分解は省略している。後でも暗黙的に2が例外扱いされる。）
f(2)=-(5+2i)(14+i)i
f(5)=-16(10+7i)(13+2i)i
f(5+4i)=16(7+10i)(25+14i)
f(11)=-64(5+4i)(2+7i)(11+6i)
f(5-2i)=-256(7+12i)
f(3-8i)=64(14+9i)(11+14i)
素因子のガウス素数はiを適当に何回か掛けて第一象限にくるように調整した。
複素数平面にこれらのガウス素数を青で、一方(1+4i)の倍数を赤でプロットした：



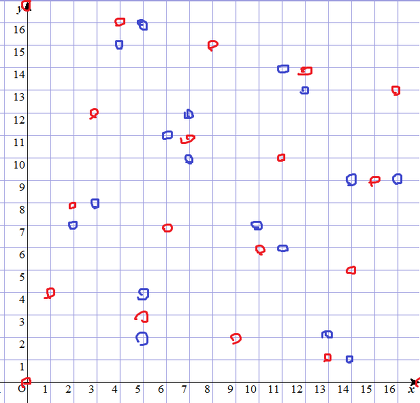p≡±1,±i (mod 1+4i) が一目瞭然である。
逆に、これを満たすpを適当にとればf(x)がpで割り切れるxが確かに存在する。

# 青でプロットされたがf(x)の分解には挙げていないガウス素数p=12+13iを確かめる。
実はf(x)がpで割り切れるxを探すには、1から12^2+13^2=313までを探せば良い。
確かにx=100,162,197,281を得る。
[補足]
剰余類Z[i]/(12+13i)Z[i] が Z/313Zに同型であることによる。
「i=-25を代入する」という操作が左から右への全単射を与える。

# もう1つ、ガウス素数かつ有理素数でこの条件式を満たす素数p=47を確かめてみる。
f(x)がpで割り切れるxが存在するかどうかは、{a+bi|a,bは0から46}を全探索すれば良い。
確かにx=23+13i, 27+37i, 33+36i, 46+28i を得る。

--
・さらに！
http://www1.kcn.ne.jp/~mkamei/math/130319_elliptic_function.pdf
27ページに書いてある記述によると
s^16+52s^12-26s^8-12s^4+1の分解体をLとすると、Gal(L/Q(i))がZ[i]/5Z[i]に同型である。
他にもいろいろ読んでいると、そういうことか、と（ある程度）理解した。

・sn(5u)の分子をf(s)とおいたときのf(s)=0の解の構造を説明する。
f(s)を再掲すると s* (s^8-2s^4+5)* (s^16+52s^12-26s^8-12s^4+1) である。

関数sn(u)は、レムニスケートの周長と関わる実定数wをつかって、
零点集合が格子点{mw+inw|m,n∈Z}となるような周期的な関数である。
より正確には、sn(u+w)=sn(u+wi)=-su(u) という関係で半周期的である。

それでf(s)=0の25個の解は、{sn(aw/5+ibw/5)|a,bは-2から2までの整数}で表せる。
そのうち a=b=0が因子sに相当し、
a+biが1±2iの倍数となるような8組が(s^8-2s^4+5)の零点を与え
残りが (s^16+52s^12-26s^8-12s^4+1) の零点である。
また、sn(iu)=i*sn(u), sn(-u)=-sn(u)等の性質から、
a+bi, -b+ai, -a-bi, b-aiの4つ組に対応する解は4乗した結果が一致する関係にある。

そこで、F(s)=s^16+52s^12-26s^8-12s^4+1=0の解の1つをαとすると
α=sn(u) となるuによって16個の解はαを使って次のように表される。
sn(u)=α,
sn(2u)=2α*sqrt(1-α^4)/(α^4+1)
sn((1+i)u) = (1+i)*α/sqrt(1-α^4)
sn((2+i)u) =  2(1+i)*α*sqrt(1-α^4)*(1+α^4) / (α^4-2α^2-1)(α^4+2α^2-1)
それらに±iあるいは-1を掛けたものを合わせてことで解の個数が16個になる。

このままではsqrt(1-α^4)が有理式じゃない
sn(5u)=0と半対称性より例えばsn(2u)=sn(3u)が成り立つことから
sqrt(1-α^4)に等しいαの有理式(α^12+7α^8+3α^4-3)/(6α^8-12α^4-2)を得る。
(実際、右側の有理式を2乗したものから(1-α^4)を引けば確かにF(α)を因数にもつ。)
このようにして、解たちをすべてαの有理式で表せた。

そうすると、ガロア群の作用を明示することもできる。
F(s)/Q(i)のガロア群は、剰余類Z[i]/5Z[i]のうち既約剰余類がなす乗法群
{±1,±2,±i,±2i,±1±i,±2±2i} (複号任意)　に自然に同型であり、
そのkという元はα=sn(u) を sn(kα)に移すように作用するわけである。

そして部分群Aに対応する中間体が、Q(i)上の対応する合同群による類体に違いない。
f(x)=x^16+52x^3-26x^2-12x+1の最小分解体は、
部分群{±1,±i}に対応する中間体というわけだったのだ。

そういうことならF(s)の素因子は、5を除いてp≡1 (mod 5)と分布することが期待される。
ところが実際に調べると19や79などが出てくる。
ガウス素数では1+20iや1+40iの他に9+10i, 29+10i のような素因子が出現する。

ここでよく考えてみると、p=9+10iではp≡4 (mod 5)であるが、
p=-9-10iとみなせばp≡1 (mod 5)である。
複素数では「正」という方向は絶対的ではないのだ。

4次剰余の相互法則の記述でprimaryという呼称で見かけた「標準形」を使うと解決した。
a+bi, -b+ai, -a-bi, b-ai の中で、2+2iを法として1に合同なものが1つだけある。
それを「標準形」として採用するのである。
具体的には、x+yiと書いて(x,y)≡(1,0)または(3,2) (mod 4)となるものを選ぶのである。

F(s)の素因子を改めて標準形で記述すると、
-19, -79, -9-10i, 1+40i, 1+20i, -29-10i 等を得る。
これらは、確かにp≡1 (mod 5)を満たすように分布する。すごい。

すなわち：

[命題1のQ(i)版]
レムニスケート関数のκ倍角の式の分子F(s)による最小分解体をLとおく。
拡大L/Qのガロア群GはZ[i]/κZ[i]の既約剰余類がなす乗法群と同一視できる。
Gの部分群Aに（ガロアの基本定理の意味で）対応する中間体をMとする。このとき
Q(i)上でf(x)の最小分解体がMとなるような多項式f(x)のガウス素因数の集合は、
標準形において、有限個の例外を除いてκZ[i]+d型素数(d∈A)全体である。

# さっきの(1+4i)倍角のf(x)についても
F(s)=f(s^4)=s^16+(12-20i)s^12+(-10+28i)s^8+(-20-12i)s^4+(1+4i) の素因数を調べると
小さいものでは10+7i, 11+6i, 4+15i, 5+16i が得られ、
標準形にすると、7-10i, 11+6i, -15+4i, 5+16i であり、
1を引いた 6-10i, 10+6i, -16+4i, 4+16i たちが(1+4i)の倍数となっている。
すなわちF(s)の素因子はp≡1 (mod 1+4i)と分布する。

--
・さらに！さらに！

f(x)=x^4+(12-20i)x^3+(-10+28i)x^2+(-20-12i)x+(1+4i)
の最小分解体は、h(x)=x^4-(1+4i) の最小分解体と一致することに気がついた。

これを本当に確認できた時は飛び上がってしまった。
実際にf(x)=0の解をαとすると
β={(3-5i)α^3+(-63-123i)α^2+(65+81i)α+(-29+71i)}/64 がβ^4 = 1+4i を満たす。
（これを得るには[2]で紹介したアルゴリズムでh(x)をQ(α)係数で因数分解した）
ちなみに逆に解けば α=(-1-2i)β^3+(3i)β^2+(1-4i)β+(-3+5i)

ガウス素数pについて以下の同値を得る。
x^4≡(1+4i) (mod p) となるxが存在
⇔ h(x)≡0 (mod p) となるxが存在
⇔ f(y)≡0 (mod p) となるyが存在[補足1]
⇔ p≡±1,±i (mod 1+4i) [先に紹介した事実]
⇔ p≡q^4 (mod 1+4i) となるqが存在 [補足2]

この結果は4次剰余の相互法則である！

[補足1]
上記のαとβの関係式と[命題4-1]による。
h(x)≡0 に対してy≡{(3-5i)x^3+(-63-123i)x^2+(65+81i)x+(-29+71i)}/64がf(y)≡0を、
f(y)≡0 に対してx≡(-1-2i)y^3+(3i)y^2+(1-4i)y+(-3+5i) が h(x)≡0 を満たす。

[補足2]
剰余類　Z[i]/(1+4i)Z[i]　の構造は　Z/17Z　と同型である。
「iに4を代入する」という操作が全単射を与える。従って上記の同値は、
「p≡±1,±4 (mod 17) ⇔ p≡q^4 (mod 17) となるqが存在」と有理整数に翻訳される。

---
・より一般に(a+bi)角に対応する類体から4次の中間体をとれば
x^4-α(αはa+bi, -b+ai, -a-bi, b-aiのどれか) の最小分解体と一致して、
同様の議論で4次剰余の相互法則を得る仕組みがあると予想される。
以下で2つの例を紹介する。
一般の場合にαが4つのうちどれになるのかの説明は、見つけられていない。

以下ではpは標準形のガウス素数とする。

・(1+2i)倍角の式
sn((1+2i)u) = s*(s^4-(1+2i))/((1+2i)s^4-1) からF(s)=s^4-(1+2i) を得る。
x^4≡1+2i (mod p)となるxが存在
⇔ F(x)≡0 (mod p) となるxが存在
⇔ p≡1 (mod 1+2i)
（⇔ p≡q^4 (mod 1+2i)となるqが存在）

# 2^4≡1+2i (mod p=15-2i) に対して実際p=1+(2-6i)(1+2i)
# p=1+(10+6i)(1+2i)=-1+26i に対して実際例えば110^4≡1+2i (mod p)

・3倍角からはF(s)=s^8+6s^4-3である。
次数4の中間体は、ガロア群をZ[i]/3Z[i]と同一視したときの部分群{1,-1}に対応する。
f(x)=x^4+6x^2-3の最小分解体がそれを与える。
そしてそれは実はx^4+3の最小分解体と一致する。
これを具体的な関係として確認するのは、やはりやりがいがある課題であった：
f(x)=0の解をαとしてβ=(α^3+5α)(1+i)/4 とおくとβ^4+3=0 という関係を得た。
そういうわけで、
x^4≡-3 (mod p)となるxが存在
⇔ f(y)≡0 (mod p)となるyが存在
⇔ p≡±1 (mod 3)
（⇔ p≡q^4 (mod 3)となるqが存在）

# 4^4≡-3 (mod -1+6i) に対して実際-1+6i≡-1 (mod 3)
# p=-7+12i に対して実際例えば13^4≡-3 (mod p)
# p=-3+8i に対しては実際 x^4≡-3 (mod p)となるxは存在しない

--
終わり