§18.一変数関数の定積分と原始関数

---

注意すべき事項は特にないと思う。
微積分学の基本定理は、有界な関数に限定して問題(18.1),(18.2)で示すことになる。
広義の原始関数は問題(18.3)で問題にされる。
変数変換(置換積分)の公式は(18.4)で示すことになる。
部分積分は問題にされていない。

---

(18.1)fは[a,b]上有界、積分可能。以下を示せ。
(1)関数F(x)=∫_a^xf(y)dy は[a,b]上一様連続である。

任意の正数εに対して|x-z|＜δならば|F(x)-F(z)|＜εとなるδを主張する。
|F(x)-F(z)|は|∫xzf(y)dy|に等しい。そこで、sup|f|([a,b])=Mとおく。
（fが有界なので|f|も有界であり上限を持つことが保証される。）
すると|F(x)-F(z)|≦M|x-z|であるから、ε/Mより小さい正数は良いδになる。

(2)c∈[a,b], fはxで連続とする。t<0でg(t)をg(t)=sup{|f(x)-f(c)|;x∈[a,b]かつ|x-c|<t}で定める。
　x∈[a,b]かつx≠cのとき |∫_c^xf(y)dy /(x-c) - f(c)|≦g(|x-c|)が成り立つ。
　これより、d/dx ∫_a^xf(y)dy|_x=c=f(c)が導かれる。

(前半)|∫cxf(y)dy /(x-c) - f(c)|=|∫cx(f(y)-f(c))dy /(x-c)|
≦∫cx|f(y)-f(c)|dy /|x-c| ≦∫cxg(|y-c|)dy /|x-c| ＝g(|x-c|)
(後半)limx→c(F(x)-F(c)) /(x-c)＝∫cxf(y)dy /(x-c)
limx→cg(|x-c|)は[(1)により]0であるから、前半の不等式より、
limx→c|∫cxf(y)dy /(x-c)-f(c)|=0
すなわちlimx→c(F(x)-F(c)) /(x-c)＝f(c)が言えたので結論を得た。

---

(18.2)f,Fは[a,b]上有界、F(x)は[a,b]上連続で(a,b)上でf(x)の原始関数である。以下を示せ。
(1)[a,b]の分割�凾ﾉ対してs(��;f)≦F(b)-F(a)≦S(��;f)

小区間Ji=[xi-1,xi]に注目する。平均値の定理を使って、ciが存在して、
F(xi)-F(xi-1)=f(ci)(xi-xi-1)とできる。
inff(Ji)≦f(ci)≦supf(Ji)であるから、
これに小区間の幅(xi-xi-1)をかけてiについて合計すれば求める不等式を得る。

(2)fは[a,b]上積分可能とする。このとき∫_a^bf(x)dx=F(b)-F(a)

|�處→0を(1)に適用すればはさみうちの原理から得る。

---

(18.3)Iは区間、F,GはI上連続。 　CはIの部分集合で、任意の[a,b]⊂Iに対してC∩[a,b]は有限集合。以下を示せ。
(1)F,GはI上でCの元を除いて微分可能でF'(x)=G'(x)とする。F(x)-G(x)はI上で定数値関数である。

h(x)=F(x)-G(x)とおく。任意のa,b∈Iに対してh(a)=h(b)を示せば十分。
C∩[a,b]は有限集合であるからそれらにa,bを追加した集合を小さいものから並べて
x0=a,x1,...,xn=bと書く。h(xi)=h(xi-1)を示せばよい。
h'(x)=F'(x)-G'(x)は常に0であるから、h(xi)≠h(xi-1)とすると、
[F,Gは連続よりhも連続、また区間(xi,xi-1)でF,G,従ってhは微分可能なので]
平均値の定理を使えてh'(x)≠0となるxがその区間に存在することになって矛盾する。

(2)fは[a,b]⊂Iで有界かつ積分可能とする。さらに、Cの元を除いてF'(x)=f(x)とする。
　　∫_a^bf(x)dx=F(b)-F(a)が成り立つ。

(1)と同じようにxiをとる。問題(18.2)より∫xi-1xi f(x)dx=F(xi)-F(xi-1)なので合計すればよい。

---

(18.4)fは区間I上の連続関数、φは区間[α,β]上の関数で次の条件を満たすとする。
・φ([α,β])⊂I, φ(α)=a かつφ(β)=b
・φは[α,β]上微分可能
・φ'は[α,β]上積分可能
このとき、∫_a^bf(x)dx=∫_α^βf(φ(t))φ'(t)dt が成り立つ

微積分学の基本定理を使う。すなわち(18.1),(18.2)が有界という条件なしに成り立つことを使う。
I上の関数F(x)を∫axf(y)dyによって定めると拡張(18.1)より、
　F(x)はI上で微分可能であり、によりF'(x)=f(x)が成り立つ。
F(φ(t))は上の２つの条件から[α,β]上微分可能であり（合成関数の微分法）
　F'(φ(t))=F'(φ(t))φ'(t)=f(φ(t))φ'(t)
また、3番目の条件と、"連続関数は積分可能"と、(17.12),(17.15)を使うと、
　f(φ(t))φ'(t)が積分可能であることが分かる。
従って拡張(18.2)によって、
　∫abf(x)dx=F(b)-F(a)
　∫αβf(φ(t))φ'(t)dt=F(φ(β))-F(φ(α))=F(b)-F(a)
が言えるので、両者が等しいことが示された。

---

[以下定義域は書いてなければ自然な定義域で、Cは積分定数。]
(18.5)f(x)の原始関数F(x)を求めよ。
(1)f(x)=sinx/1+cos²x
cosx=cと置換する。F(x)=-Arctan(cosx)+C
(2)f(x)=e^x/(e^x+1)²
e^x+1=yと置換する。F(x)=-1/(e^x+1)+C
(3)f(x)=logx/x I=(0,∞)
logx=y, F(x)=(logx)²/2+C
(4)f(x)=1/xlogx I=(1,∞)
logx=y, F(x)=log(logx)+C
(5)f(x)=Arctanx/(1+x²)
Arctanx=y, F(x)=(Arctanx)²/2+C
(6)f(x)=x³√1-x²
1-x²=y, f(x)dx=(y-1)√ydy, F(x)=1/5 (1-x²)^5/2 - 1/3 (1-x²)^3/2
途中正しくはf(x)dx=1/2 (1-y)√ydy

---

(18.6)f(x)の原始関数F(x)を求めよ。
(1)f(x)=1/(x²-1)² 　(2)f(x)=x/(x²-2x+2) 　(3)f(x)=1/(x³-1)
初回の通り。 [(1) 　(2) 　(3)]

---

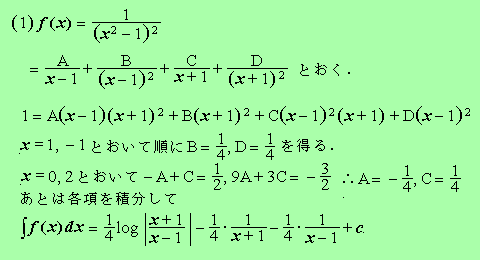
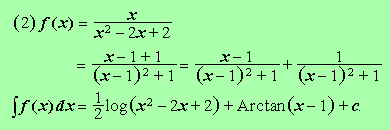
(18.7)同じく初回の通り。 (18.7)

---

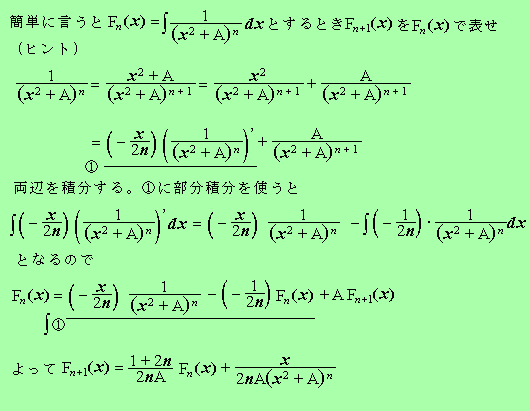
(18.8)f(x)の原始関数F(x)を求めよ。
(1)f(x)=1/cosx　(2)f(x)=sinx/(1+sinx) 　(3)f(x)=1/(a²cos²-b²sin²x)
(1)は講義の練習問題、(2),(3)は初回にあった。 [(1) 　(2) 　(3)]

---

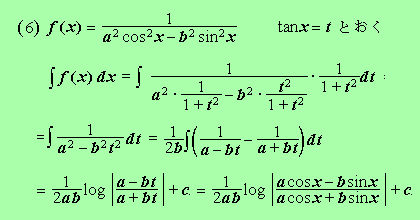
(18.9)f(x)の原始関数F(x)を求めよ。
(1)f(x)=e^-x/(e^2x+1)
これも初回。(1)
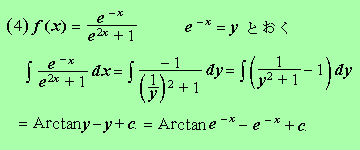
(2)f(x)=(ae^x+be^-x) / (e^x-e^x-)
...分子を(a+b)(e^x+e^x-)/2 + (a-b)(e^x-e^x-)/2 と変形するのが早い。
第一項は分母を丸ごと置換できて、答えはa+b/2 log|e^x-e^x-| + a-b/2 x +C
あるいは例えばa/2 log|e^2x-1| + b/2 log|1-e^-2x|+Cのように書くこともできる。

---

(18.10)A≠0とする。
(1)f(x)=1/√(x²+A)の原始関数F(x)を求めよ。
...マニュアル通りに√(x²+A)-x=tと置く。
[x=(t²-A)/2t, dx/dt=(t²+A)/2t², t-x=(t²+A)/2t]
∫f(x)dx=...=∫1/t dt=log|t|+C=log|√(x²+A)-x|+C

(2)f_n(x)=xⁿ/√(x²+A)の原始関数をF_n(x)と書く。自然な漸化式を求めよ。
...(ヒントの等式)f_n+2(x)=xⁿ⁺¹d/dx√(x²+A)=d/dx{xⁿ⁺¹√(x²+A)}-(n+1)xⁿ√(x²+A)
それを両辺積分する。最後の項はxⁿ√(x²+A)=xⁿ(x²+A)/√(x²+A)=f_n+2(x)+Af_n(x)
F_n+2(x)=xⁿ⁺¹√(x²+A)-(n+1){F_n+2(x)+AF_n(x)}
整理してF_n+2(x)={xⁿ⁺¹√(x²+A)-A(n+1)F_n(x)}/(n+2)となった。

---

(18.11)(a,b)≠(0,0)とする。
(1)f(x)=xe^axcosbxの原始関数F(x)を求めよ。

G'(x)=eaxcosbxとおくとF(x)=xG(x)-∫G(x)dx
G(x)を適当に求めると{beaxsinbx+aeaxcosbx}/(a2+b2)
（考え方はeaxsinbx と eaxcosbx を微分して比べるのが早いかな）
F(x)=x{beaxsinbx+aeaxcosbx}/(a2+b2)-{2abeaxsinbx+(a2-b2)eaxcosbx}/(a2+b2)2

(2)α≠0とする。f_n(x)=xⁿe^αxの原始関数をF_n(x)を表す。自然な漸化式を求めよ。

Fn+1=1/α xn+1eαx-∫(n+1)/α xneαxdx
=1/α xn+1eαx-(n+1)/α Fn(x)

(3)α+1≠0とする。g_n(x)=x^α(logx)ⁿの原始関数をG_n(x)と表す。自然な漸化式を求めよ。

Fn+1=1/(α+1) xα+1(logx)n+1-∫(n+1)/(α+1) xα(logx)ndx
=1/(α+1) xα+1(logx)n+1-(n+1)/(α+1) Fn(x)

---

(18.12)Iは区間、fはIで連続、a∈I。I上の関数列F_n (n≧0)を次のように定める。
　　F₀(x)=f(x), F_n+1(x)=∫_a^xF_n(t)dt
(1)F_n+1(x) を x^k∫_a^xt^n-kf(t)dt (0≦k≦n) の線形結合で表せ。

[余剰項の積分表示を関数Fn+1に対して用いる。]
Fn+1(x)のk次導関数がFn+1-k(x)であることにより、
Fn+1(x)=Σ0≦k≦n1/k! Fn+1-k(a) (x-a)k + Rn+1(x)
余剰項を積分表示するとRn+1(x)=1/n! ∫axF0(t)(x-t)ndt
ところで漸化式から、n＞0に対してFn(a)=0であることが分かるから、
Fn+1(x)=1/n! ∫axF0(t)(x-t)ndt=1/n! ∫axf(t)(x-t)ndt
=Σ0≦k≦n(-1)n-knCk/n! xk∫axtn-kf(t)dt

(2) (1)の結果を用いて、(イ)(ロ)(ハ)の不定積分を求めよ。
(イ)∫₁^xlogtdt

(1)でf(x)=1/x, a=1とすれば∫1xf(t)dt=logxであるから、
F1+1(x)=-∫1xdt+x∫1x1/t dt
=-(x-1)+x(logx-log1)=xlogx-x+1を得る。

(ロ)∫₀^xlog(1+t²)dt

f(x)=2x/1+x2,a=0とすればよい。
F1+1(x)=-∫0x2t2/(1+t2)dt+x∫0x2t/(1+t2)dt
=∫0x2{1/(1+t2)-1}dt + xlog(1+x2)
=2Arctanx+xlog(1+x2)-2x

(ハ)∫₀^xArctantdt

f(x)=1/1+x2,a=0。
F1+1(x)=-∫0xt/(1+t2)dt+x∫0x1/(1+t2)dt
=-1/2 log(1+x2)+xArctanx

（このような２次原始関数を求める場合はx'f(x)と見て部分積分するのと似ている）

---

---

戻る