４

§18.一変数関数の定積分と原始関数(続き)

気合が必要。より簡単に変形できるかもしれないし間違っているかもしれない。

(18.13)積分せよ。
$\\\mbox{(1)}f(x)=\frac{x^2+3x+4}{x^2+6x+8}=1-\frac{3x+4}{(x+2)(x+4)} =1-\frac{1}{x+2}+\frac{4}{x+4}\\ \int f(x)dx=x-\log|\frac{x+4}{x+2}|+A\\ \\\mbox{(2)}f(x)=\frac{x+1}{x^3+x^2-6x}= -\frac{\frac{1}{6}}{x}-\frac{\frac{2}{15}}{x+3}+\frac{\frac{3}{10}}{x-2}\\ \int f(x)dx=\frac{3}{10}\log|x-2|-\frac{1}{6}\log|x|-\frac{2}{15}\log|x+3|+A =\log|\frac{(x-2)^9}{x^5(x+3)^4}|+A\\ \\\mbox{(3)}f(x)=\frac{x^2}{x^4-1}=\frac{\frac{1}{4}}{x-1}-\frac{\frac{1}{4}}{x+1} +\frac{\frac{1}{2}}{x^2+1}\\ \int f(x)dx=\frac{1}{4}\log|\frac{x-1}{x+1}|+\frac{1}{2}\mbox{Arctan}x\\ \\\mbox{(4)}f(x)=\frac{1}{x^4+1} =\frac{\frac{1}{2\sqrt2}x+\frac{1}{2}}{x^2+\sqrt2x+1} +\frac{-\frac{1}{2\sqrt2}x+\frac{1}{2}}{x^2-\sqrt2x+1}\\ =\frac{\frac{1}{4\sqrt2}(2x+\sqrt2)+\frac{1}{4}}{x^2+\sqrt2x+1} -\frac{\frac{1}{4\sqrt2}(2x-\sqrt2)+\frac{1}{4}}{x^2-\sqrt2x+1}\\ \int f(x)dx=\log\frac{x^2+\sqrt2x+1}{x^2-\sqrt2x+1}\\ +\frac{1}{2\sqrt2}\mbox{Arctan}(\sqrt2x+1) +\frac{1}{2\sqrt2}\mbox{Arctan}(\sqrt2x-1)$

(18.14)積分せよ。
$\\\mbox{(1)}f(x)=\frac{1}{x^n(1-ax)}= \frac{q_0}{1-ax}+\frac{q_1}{x}++\frac{q_2}{x^2}+\cdots+\frac{q_2}{x^n}$
分母を払って $x=\frac{1}{a}$ とおくと $q_0=a^n$ を得る。
あとは $x$ の最高次から係数を比較して $q_i=a^{n-i}$ を次々と得る。
$\int f(x)dx=a^{n-1}\log|\frac{x}{1-ax}|-\sum_{k=1}^{n-1}\frac{a^{n-1-k}}{kx^k}+A$
$\\\mbox{(2)}f(x)=\frac{x^5}{(1+x^2)^3}$
$1+x^2=y$ とおくと $2x=dy/dx$
$\int f(x)dx=\int \frac{(y-1)^2}{2y^3}dy=\frac{1}{2}\log y+\frac{1}{y}-\frac{1}{4y^2}+A \\=\frac{1}{2}\log(1+x^2)+\frac{3-x^3}{4(1+x^2)}+A\\ \\\mbox{(3)}f(x)=\frac{x^4}{(1+x^2)^3}$
$x=\tan\theta$ とおくと $\frac{1}{1+x^2}=d\theta/dx$
$\int f(x)dx=\int\frac{\tan^4\theta}{(1+\tan^2\theta)^2}d\theta =\int\sin^4\theta d\theta=\cdots\\ =-\frac{1}{4}\sin^3\theta\cos\theta-\frac{3}{8}\sin\theta\cos\theta-\frac{3}{8}\theta+A\\ =-\frac{(5x^2+3)x}{8(1+x^2)^2}-\frac{3}{8}\mbox{Arctan}x+A\\$
$\\\mbox{(4)}f(x)=\frac{1}{x^3(1+x^2)^3}$
$\frac{1}{1+x^2}=y$ とおく。 $\int f(x)dx=\int\frac{y^3}{2(y-1)^2}dy$
$y-1=z$ とおく。 $\int\frac{y^3}{2(y-1)^2}dy=\int\frac{z^3+3z^2+3z+1}{2z^2}dz$
$\\=z^2+\frac{3}{2}z+\frac{3}{2}\log|z|-\frac{1}{2z}+A\\ =\frac{x^4}{(1+x^2)^2}-\frac{3x^2}{1+x^2}+\frac{1+x^2}{2x^2}+\frac{3}{2}\log\frac{x^2}{1+x^2}+A\\ =\frac{1+3x^2}{2x^2(1+x^2)^2}+\frac{3}{2}\log\frac{x^2}{1+x^2}+A\\$

(18.15)積分せよ。 $0<|a|<1, \theta_0=\mbox{Arcsin}a$
$\\\mbox{(1)}f(x)=\frac{a}{a-\sin x}\;\;I=[-\pi-\theta_0,\theta_0]\mbox{ or }[\theta_0,\pi-\theta_0]$
$k$ を整数として $(2k-1)\pi<x<(2k+1)\pi$ の範囲で $\tan\frac{x}{2}=t$ と置換積分する。
$\int f(x)dx=\int \frac{a}{a-\frac{2t}{1+t^2}}\frac{2}{1+t^2}dt=\int\frac{2dt}{(t+1/a)^2-(1/a^2-1)}\\ =\frac{1}{\sqrt{1/a^2-1}}\int\left(\frac{1}{(t-1/a)-\sqrt{1/a^2-1}}-\frac{1}{(t+1/a)+\sqrt{1/a^2-1}}\right)dt\\ =\frac{a}{\sqrt{1-a^2}}\log\biggr|\frac{t-1/a-\sqrt{1/a^2-1}}{t-1/a+\sqrt{1/a^2-1}}\biggr|+A\\ =\frac{a}{\sqrt{1-a^2}}\log\biggr|\frac{a\sin(x/2)-(1+\sqrt{1-a^2})\cos(x/2)}{a\sin(x/2)-(1-\sqrt{1-a^2})\cos(x/2)}\biggr|+A$
これは、logの中身の分子または分母が0でない限り連続であるが、
実はそうなるのはsinx=aであるときに限ることが分かるので良いF(x)となる。
a=1/2, A=0の時のグラフを参考に示す。[赤:f(x), 青:F(x)]

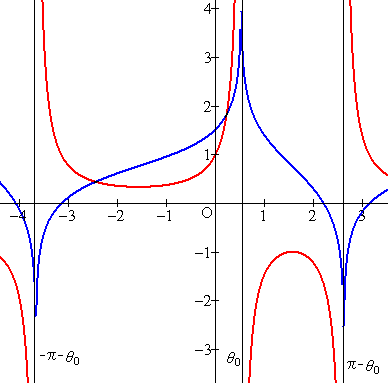
$\\\mbox(2)f(x)=\frac{1-a^2}{1-2a\cos x+a^2}\;\;I=[-\infty,+\infty]$
(1)と同様に $k$ を整数として $(2k-1)\pi<x<(2k+1)\pi$ の範囲で $\tan\frac{x}{2}=t$ と置換積分する。
$\\\int f(x)dx=\int\frac{1-a^2}{1-2a\frac{1-t^2}{1+t^2}+a^2}\frac{2}{1+t^2}dt\\ =\int\frac{2(1-a^2)}{(1+a)^2t^2+(1-a)^2}dt\\ =2\int\frac{\frac{1-a}{1+a}}{t^2+\left(\frac{1-a}{1+a}\right)^2}dt\\ =2\mbox{Arctan}\left(\frac{1+a}{1-a}}\tan\frac{x}{2}\right)+A$
これをF(x)とし、a=1/2, A=0としてグラフを書くと、下のようである[赤:f(x), 青:F(x)]

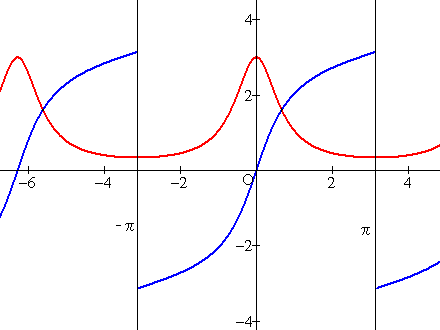
例えばx→π-0でのF(x)の極限を考えるとtan(x/2)→+∞だからArctan(*)→π/2でF(x)→π
同様にx→π+0でのF(x)の極限を考えるとtan(x/2)→-∞だからArctan(*)→-π/2でF(x)→-π
従ってF(x)を以下のように定めればF(x)は[-∞,+∞]で連続となるので求めるものとなる:
$F(x)=\biggr\{\begin{array}{ll} 2\mbox{Arctan}(\frac{1-a}{1+a}\tan\frac{x}{2})+2k\pi+A&(\;(2k-1)\pi<x<(2k+1)\pi\;)\\ (2k+1)\pi+A&(\;x=(2k+1)\pi\;)\end{array}$

(18.16)(a,b)≠(0,0)である。
$\\F_1(x)=x,\;F_2(x)=\log|a\cos x+b\sin x+c|,F_3(x)=\int\frac{1}{a\cos x+b\sin x+c}dx$
とする。
$\\\mbox{(1)}f(x)=\frac{a'\cos x+b'\sin x+c'}{a\cos x+b\sin x+c}$ の原始関数は
$1,F_1(x),F_2(x),F_3(x)$ の線形結合で表せることを示せ。
$F_i'(x)=f_i(x)$ と書く。 $f(x)=\sum_ip_if_i(x)$ と仮定する。それらは、
$\biggr\{\begin{array}{ccccc}ap_1&+&bp_2&=&a'\\bp_1&-&ap_2&=&b'\\cp_1&+&p_3&=&c'\end{array}$
を満たせばよい。具体的に、
$p_1=\frac{aa'+bb'}{a^2+b^2},\;p_2=\frac{ba'-ab'}{a^2+b^2},\;p_3=c'-cp_1$
と求められ、これらによって得られる $\sum_ip_iF_i(x)$ はf(x)の原始関数となる。
$\\\mbox{(2)}\int\frac{\cos x}{a\cos x+b\sin x}dx$ を求めよ。
前問に係数たちを代入する。
$\\p_1=\frac{a}{a^2+b^2},\;p_2=\frac{b}{a^2+b^2},\;p_3=0\\ \int g(x)dx=\frac{ax+b\log|a\cos x+b\sin x|}{a^2+b^2}+A$

(18.17)k,m,nは整数。 $I=(k\frac{\pi}{2},(k+1)\frac{\pi}{2})$ とする。
関数 $\sin^mx\cos\nx$ のI上での原始関数を $F_{m,n}(x)$ と表す。
この時、定数差を除いて、(1),(2)の等式が成り立つことを部分積分等を用いて導け
$\\\mbox{(1)}(m+n)F_{m,n}(x)=\sin^{m+1}x\cos^{n-1}+(n-1)F_{m,n-2}(x)\\ \mbox{(2)}(m+n)F_{m,n}(x)=-\sin^{m-1}x\cos^{n+1}+(m-1)F_{m-2,n}(x)$
m≠-1の時、部分積分を使って
$(m+1)\int\sin^mx\cos\nxdx=\sin^{m+1}x\cos^{n+1}x+\int(n-1)\sin^{m+2}x\cos\{n-2}xdx$
しかしながら、m=-1を代入してもこの式は成り立つことが分かるので一般に、 $F_{m,n}(x)=\sin^{m+1}x\cos^{n+1}x+(n-1)(F_{m,n-2}(x)-F_{m,n}(x))$
$(sin^2x=1-\cos^2x)\\$ を使った。整理して求める式を得る。(2)も同様だろう。

(18.18) $I_{m,n}=\int_0^{\pi/2}\sin^mx\cos^nxdx\;(m,n=0,1,2,\cdots)$ と定める。
$\\\mbox{(1)}I_{0,0}=\frac{\pi}{2},\;I_{0,1}=I_{1,0}=1,\;I_{1,1}=[-\frac{1}{4}\cos 2x]_0^{\pi/2}=\frac{\pi}{4}$
$\\\mbox{(2)}n\geq2$
$(m+n)I_{m,n}=[\sin^{m+1}x\cos^{n-1}x]_0^{\pi/2}+(n-1)I_{m,n-2}=(n-1)I_{m,n-2}$
従って、 $I_{m,n}=\frac{n-1}{m+n}I_{m,n-2}$ を得る。
$\\\mbox{(3)}I_{m,n}=\biggr\{\begin{array}{ll} \frac{n-1}{m+n}\frac{(n-2)-1}{m+(n-2)}\cdots\frac{1}{m+2}I_{m,0}(x)&(n=0,2,4,\cdots)\\ \frac{n-1}{m+n}\frac{(n-2)-1}{m+(n-2)}\cdots\frac{2}{m+3}I_{m,1}(x)&(n=1,3,5,\cdots) \end{array}$
mについても同様なので、よく考えれば、!!を使って次のように書ける。
$I_{m,n}=\frac{(m-1)!!(n-1)!!}{(m+n)!!}I_{m\%2,n\%2}$
[m%2,n%2はそれぞれm,nを2で割ったあまりを意味する。]

(18.19)a>0, nは整数, I=(-a,0)あるいは(0,a)
$f_n(x)=\frac{x^n}{\sqrt{a^2-x^2}}$ のI上での原始関数を $F_n(x)$ と表す
(1)関数 $F_{-1}(x),F_0(x)$ を求めよ。
(n=-1)√を丸ごとyとおく。
$\int\frac{1}{x\sqrt{a^2-x^2}}dx=\int\frac{1}{a^2-y^2}dy\\ =\frac{1}{2a}\int\left(\frac{1}{a-y}-\frac{1}{a+y}\right)dy\\ =\frac{1}{2a}\log\biggr|\frac{a-\sqrt{a^2-x^2}}{a+\sqrt{a^2-x^2}}\biggr|+A\\$
(n=0)Arcsinの導関数を思い出す。
$\int\frac{1}{\sqrt{a^2-x^2}}dx=\mbox{Arcsin}x+A$
(2),(3)n≧0及びn＜0の時に対して自然な漸化式を得よ。
ヒントの等式:
$f_n(x)=-x^{n-1}\frac{d}{dx}\sqrt{a^2-x^2}=-\frac{d}{dx}(x^{n-1}\sqrt{a^2-x^2}) +(n-1)x^{n-2}\sqrt{a^2-x^2}$ ここで、 $x^{n-2}\sqrt{a^2-x^2}=\frac{a^2x^{n-2}}{a^2-x^2}-\frac{x^n}{a^2-x^2}=a^2f_{n-2}(x)-f_n(x)$
最終項にこれを代入して両辺を積分して整理する。
$\\F_{n+2}(x)=-\frac{1}{n+2}x^{n+1}\sqrt{a^2-x^2}+\frac{n+1}{n+2}a^2F_n(x)\\ F_{n-2}(x)=\frac{1}{n-1}x^{n-1}\sqrt{a^2-x^2}+\frac{n}{n-1}F_n{}$

(18.20)a<b。積分せよ。
$\\\mbox{(1)}\int\sqrt\frac{b-x}{x-a}dx$
√を丸ごとtとおく。逆に解いて、
$x=\frac{b+at^2}{1+t^2},\;\frac{dx}{dt}=-\frac{2(b-a)t}{(1+t^2)^2}\\ \int tdx=-\int\frac{2(b-a)t^2}{1+t^2}dt\;\;[t=\tan\theta]\\ =-2(b-a)\int\frac{\tan^2\theta}{(1+\tan^2\theta)^2}d\theta =-2(b-a)\int\sin^2\theta\cos^2\theta d\theta=\cdots\\ =(b-a)\left(\frac{1}{2}\sin\theta\cos^3\theta-\frac{1}{4}\sin\theta\cos\theta-\frac{1}{4}\theta\right)+A\\ =(b-a)\left(\frac{1}{2}\cdot\frac{t}{(1+t^2)^2}-\frac{1}{4}\cdot\frac{t}{1+t^2}-\frac{1}{4}\mbox{Arctan}t\right)+A\\ =\frac{1}{4}\left(\frac{1-t^2}{(1+t^2)^2}t+\mbox{Arctan}t\right)+A=\cdots\\ =\frac{2x-a-b}{4(b-a)}\sqrt{(x-a)(b-x)}+\mbox{Arctan}\sqrt{\frac{x-a}{b-x}}+A$

$\\\mbox{(2)}\int\frac{x}{\sqrt{(x-a)(b-x)}}dx =\int\frac{x}{b-x}tdx\;\;[t=\sqrt{\frac{b-x}{x-a}}]\\ =\int\frac{b+at^2}{1+t^2}\biggr/\bigr(b-\frac{b+at^2}{1+t^2}\bigr) \cdot t\cdot-\frac{2(b-a)t}{(1+t^2)^2}dt\\ =-2\int\frac{b+at^2}{(1+t^2)^2}dt =-2\int(a\sin^2\theta+b\cos^2\theta)d\theta\\ =\frac{a+b}{2}\sin 2\theta-(b-a)\theta+A\\ =(b+a)\frac{t}{1+t^2}-(b-a)\mbox{Arctan}t+A\\ =\frac{b+a}{b-a}\sqrt{(x-a)(b-x)}-(b-a)\mbox{Arctan}\sqrt{\frac{b-x}{x-a}}+A$

$\\\mbox{(3)}\int\frac{1}{1-\sqrt{1-x^2}}dx=\int\frac{1+\sqrt{1-x^2}}{x}dx\\$
[第二項で√を丸ごとtとおく]
$=\cdots=\log|x|-\int\frac{t^2}{1-t^2}dt\\ =\log|x|+\frac{1}{2}\log\frac{1-t}{1+t}+t+A\\ =\log|x|+\log\bigr|\frac{1-\sqrt{1-x^2}}{x}\bigr|+\sqrt(1-x^2)+A\\ =\log(1-\sqrt{1-x^2})-\sqrt{1-x^2}+A$

$\\\mbox{(4)}\int\frac{1}{(1+x^2)\sqrt{1-x^2}}\;\;[\sqrt{\frac{1+x}{1-x}}=t]\\ =\int\frac{1}{\frac{2t^2}{1+t^2}\cdot\frac{2(1+t^4)}{(1+t^2)^2}}\cdot t\cdot\frac{4t}{(1+t^2)^2}dt\\ =\int\frac{1+t^2}{1+t^4}dt =\int\left(\frac{1/2}{1+\sqrt2+t^2}+\frac{1/2}{1-\sqrt2+t^2}\right)dt\\ =\frac{1}{\sqrt2}\left(\mbox{Arctan}(\sqrt2\sqrt{\frac{1+x}{1-x}}+1) +\mbox{Arctan}(\sqrt2\sqrt{\frac{1+x}{1-x}}-1)\right)+A$

(18.21)a<b。積分せよ。
$\\\mbox{(1)}\int\sqrt\frac{x-b}{x-a}dx\;\;[t=\sqrt\frac{x-b}{x-a}]\\ =\int t\cdot\frac{2(b-a)t}{(t^2-1)^2}dt\\ =\frac{b-a}{2}\int\left(\frac{1}{t-1}-\frac{1}{t+1}+\frac{1}{(t-1)^2}+\frac{1}{(t+1)^2}\right)dx\\ =\frac{b-a}{2}\left(\log\biggr|\frac{t-1}{t+1}\biggr|-\frac{1}{t-1}-\frac{1}{t+1}\right)+A\\ =\log\biggr|\frac{\sqrt{x-b}-\sqrt{x-a}}{\sqrt{x-b}+\sqrt{x-a}}\biggr|+\frac{\sqrt{(x-a)(x-b)}}{2}+A$

$\\\mbox{(2)}\int\frac{1}{x\sqrt{x^2-x-a}}dx\;\;[t=\sqrt{x^2-x+1}-x]\\ =\int\frac{1}{\frac{1-t^2}{1+2t}\cdot\frac{t^2+t+1}{1+2t}}\cdot\frac{-2(t^2+t+1)}{(1+2t)^2}dt\\ =\int\frac{2}{t^2-1}dt=\log\biggr|\frac{t-1}{t+1}\biggr|+A\\ =\log\biggr|\frac{\sqrt{x^2-x+1}-x-1}{\sqrt{x^2-x+1}-x+1}\biggr|+A$

$\\\mbox{(3)}\int\frac{1}{x+\sqrt{x^2+x+1}}dx\;\;[t=x+\sqrt{x^2+x+1}]\\ =\int\frac{1}{t}\cdot\frac{2(t^2+t+1)}{(1+2t)^2}dt =\int\left(\frac{2}{t}-\frac{3}{1+2t}-\frac{3}{(1+2t)^2}\right)dt\\ =2\log|t|-\frac{3}{2}\log(1+2t)+\frac{3}{2(1+2t)}+A\\ =2\log|x+\sqrt{x^2+x+1}|-\frac{3}{2}\log(1+2x+2\sqrt{x^2+x+1})\\ +\frac{3}{2(1+2x+2\sqrt{x^2+x+1})}+A\\$

$\\\mbox{(4)}\int\frac{1}{1+\sqrt{x^2-1}}dx\;\;\mbox[t=x+\sqrt{x^2-1}]\\ \mbox{[}x=\frac{t^2+1}{2t},\;\frac{dx}{dt}=\frac{1-1/t^2}{2}]\\ =\int\frac{1}{1+t-x}\cdot\frac{1-1/t^2}{2}dt\\ =\int\frac{t^2-1}{(t^2+2t-1)t}dt =\int\left(\frac{1}{t}+\frac{1/\sqrt2}{t+1+\sqrt2}-\frac{1/\sqrt2}{t+1-\sqrt2}\right)dt\\ =\log|t|+\frac{1}{\sqrt2}\frac{t+1+\sqrt2}{t+1-\sqrt2}+A\\ =\log|x+\sqrt{x^2-1}|+\frac{1}{\sqrt2}\log\biggr|\frac{x+\sqrt{x^2-1}+a+\sqrt2}{x+\sqrt{x^2-1}+a-\sqrt2}\biggr|+A\\$
第二項のlogの中身の分母分子に適当に同じものをかけた変形を２つ示しておく:
$\\\log\biggr|\frac{x+\sqrt{x^2-1}+1+\sqrt2}{x+\sqrt{x^2-1}+1-\sqrt2}\biggr| =\log\biggr|\frac{x+\sqrt2\sqrt{x^2-1}}{x-\sqrt2}\biggr| =\log\biggr|\frac{\sqrt{x^2-1}-\sqrt2x-1}{1+\sqrt{x^2-1}}\biggr|$

(18.22)a,b,α,βは実数、(a,b)≠(0,0)≠(α,β)とする。
$\\\mbox{(1)}\frac{d}{dx}(\alpha_{n+1}e^{ax}\cos bx+\beta_{n+1}e^{ax}\sin bx)\\ =(a\alpha_{n+1}+b\beta_{n+1})e^{ax}\cos bx+(-b\alpha_{n+1}+a\beta_{n+1})e^{ax}\sin bx$
$\alpha_{n}e^{ax}\cos bx+\beta_{n}e^{ax}\sin bx$ と比較して逆に解けば、
$\left(\begin{array}{c}\alpha_{n+1}\\\beta_{n+1}\end{array}\right)= \frac{1}{a^2+b^2}\left(\begin{array}{cc}a&b\\-b&a\end{array}\right) \left(\begin{array}{c}\alpha_{n}\\\beta_{n}\end{array}\right)$
$\\\mbox{(2)}G_n(x)=\alpha_{n}e^{ax}\cos bx+\beta_{n}e^{ax}\sin bx$ とする。
設定より, $\frac{d}{dx}G_{i+1}(x)=G_i(x)$ である。
$\\\int\frac{x^n}{n!}G_0(x)dx=\frac{x^n}{n!}-\int\frac{x^{n-1}}{(n-1)!}G_1(x)dx$
のように部分積分を繰り返せば、最終的に、
$=\sum_{k=0}^n\frac{(-1)^kx^{n-k}}{(n-k)!}G_{k+1}(x)+A$

(18.23)前問の形に変形して積分せよ。α≠0。
$\\\mbox{(1)}\int\sin(\log x)dx=\int\sin y e^y dy\;\;[x=e^y]\\ =-\frac{1}{2}e^y\cos y+\frac{1}{2}e^y\sin\y+A\\ =-\frac{1}{2}x\cos(\log x)+\frac{1}{2}\sin(\log x) +A\\ \mbox{(2)}\int\cos\sqrt{x}dx=\int\cos y\cdot 2ydy\;\;[\sqrt{x}=y]\\ =2y\sin y+2\cos y+A=2\sqrt{x}\sin\sqrt{x}+2\cos\sqrt{x}+A\\$
$\\\mbox{(3)}\int e^{\alpha\sqrt{x}}dx=\int e^{\alpha y}\cdot 2ydy\;\;[\sqrt{x}=y]\\ =\frac{2}{\alpha}ye^{\alpha y}-\frac{2}{\alpha^2}e^{\alpha y}+A\\ =\frac{2\sqrt{x}}{\alpha}e^{\alpha\sqrt{x}}-\frac{2}{\alpha^2}e^{\alpha\sqrt{x}}+A\\ \mbox{(4)}\int e^{\sqrt[3]{x}}dx=\int e^y\cdot 3y^2dy\;\;[\sqrt[3]{x}=y]\\ =(3y^2-6y+6)e^y+A=3e^{\sqrt[3]{x}}(\sqrt[3]{x^2}-2\sqrt[3]{x}+2)+A\\$
$\\\mbox{(5)}\int x(\mbox{Arcsin}x)^2 dx=\int\siny\cdot y\cdot\cos ydy\;\;[\mbox{Arcsin}x=y]\\ =\int\frac{y^2}{2}\sin 2ydy =-\frac{1}{4}\cos 2y+\frac{1}{4}\sin 2y+\frac{1}{8}\cos 2y+A=\cdots\\ \mbox{[}\cos y=\sqrt{1-x^2},\;\sin 2y=2x\sqrt{1-x^2},\;\cos 2y=1-x^2]\\ =\frac{1}{4}(2x^2-1)(\mbox{Arcsin}x)^2+\frac{1}{2}x\sqrt{1-x^2}\mbox{Arcsin}x-\frac{1}{4}x^2+A$

(18.24)積分せよ。α≠0。
$\\\mbox{(1)}\int x^3e^{\alpha x^2}dx =\int\frac{1}{2}ye^{\alpha y}dy\;\;[x^2=y]\\ =\frac{1}{2a}ye^{\alpha y}-\frac{1}{2\alpha^2}e^{ay}+A\\ =\frac{1}{2a}x^2e^{\alpha x^2}-\frac{1}{2\alpha^2}e^{\alpha x^2}+A\\ \mbox{(2)}\int\sin x\log(\sin x)dx\\ =-\cos x\log(\sin x)-\int\left(-\cos x\frac{\cos x}{\sin x}\right)dx\\$
第二項は分母分子にsinxをかけてc=cosxと置換すれば、
$\int\cos x\frac{\cos x}{\sin x}dx=\int\frac{-c^2}{1-c^2}dc\\ =\int\left(1-\frac{1}{1-c^2}\right)dc=c+\frac{1}{2}\log\frac{1-c}{1+c}+A$
と積分されるのでこれを元の式に代入して次のようになる。
$\cos x+\frac{1}{2}\log\frac{1-\cos x}{1+\cos x}-\cos x\log(\sin x)+A$
例によって第二項は半角公式を使ってtanで書くこともできる。
$\\\mbox{(3)}\int\frac{\log(1+x^2)}{x^2}dx\\ =-\frac{1}{x}\log(1+x^2)-\int\left(-\frac{1}{x}\cdot\frac{2x}{1+x^2}\right)dx\\ =-\frac{1}{x}\log(1+x^2)+2\mbox{Arctan}x+A$
$\\\mbox{(4)}\int x^2\mbox{Arctan}xdx\\ =\frac{1}{3}\mbox{Arctan}x-\int\frac{1}{3}x^3\frac{1}{1+x^2}dx\;\;[y=1+x^2]\\ =\frac{1}{3}\mbox{Arctan}x-\frac{1}{6}\int\frac{y-1}{y}dy\\ =\frac{1}{3}\mbox{Arctan}x-\frac{1}{6}x^2+\frac{1}{6}\log(1+x^2)+A$
$\\\mbox{(5)}\int\frac{1}{\sqrt{1+x}}\mbox{Arccsin}xdx\\ =2\sqrt{1+x}\mbox{Arccsin}x-\int 2\sqrt{1+x}\frac{1}{\sqrt{1-x^2}}dx\\ =2\sqrt{1+x}\mbox{Arccsin}x-4\sqrt{1-x}+A\\$

(18.25)積分せよ。a＞0。
$\\\mbox{(1)}\int\frac{\sqrt{1+x}}{x}dx=\int\frac{y}{y^2-1}\cdot2ydy\;\;[y=\sqrt{1+x}]\\ =\int\left(2+\frac{2}{y^2-1}\right)dy=2y+\log\frac{y-1}{y+1}+A\\ =2\sqrt{1+x}+\log\frac{\sqrt{1+x}-1}{\sqrt{1+x}+1}+A\\ \mbox{(2)}\int\frac{1}{\sqrt{x}(1+\sqrt[3]{x}}dx=\int\frac{1}{y^3(1+y^2)}\cdot 6y^5dy\;\;[y=\sqrt[6]{x}]\\ =\int\left(6-\frac{6}{1+y^2}\right)dy=6y-6\mbox{Arctan}y+A\\ =6\sqrt[6]{x}-6\mbox{Arctan}\sqrt[6]{x}+A\\$
$\\\mbox{(3)}\int\sqrt{1+e^x}=\int\frac{\sqrt{1+y}}{y}dy\;\;[y=e^x]$
[(1)と同じ] $=2\sqrt{1+e^2}+\log\frac{\sqrt{1+e^x}-1}{\sqrt{1+e^x}+1}+A$
$\\\mbox{(4)}\int\log(1+\sqrt{x})dx\\ =x\log(1+\sqrt{x})-\int x\cdot\frac{1}{1+\sqrt{x}}\cdot\frac{1}{2\sqrt{x}}dx$
第二項はy=√xと置換積分すれば、
(第二項) $=\int\frac{y^2}{1+y}dy=\int\left(\frac{1}{1+y}-1+y\right)dy$
$=\log(1+y)-y+\frac{1}{2}y^2$ となるのでこれを代入して次のようになる。
$(x-1)\log(1+\sqrt{x})+\sqrt{x}-\frac{1}{2}x+A$
$\\\mbox{(5)}\int\frac{x}{\sqrt{x^4-4}}dx=\int\frac{dy}{2\sqrt{y^2-1}}\;\;[y=x^2/2]\\ =\frac{1}{2}\log(y+\sqrt{y^2-1})+A=\frac{1}{2}\log(x^2+\sqrt{x^4-1})+A$
$\\\mbox{(6)}\int\mbox{Arcsin}\sqrt{\frac{x}{x+a}}dx\;\;[y=\sqrt{\frac{x}{x+a}}]\\ \mbox{[}x=\frac{ay^2}{1-y^2},\;\frac{dx}{dy}=\frac{2ay}{(1-y^2)^2}]\\ =\int\mbox{Arcsin}y\cdot\frac{2ay}{(1-y^2)^2}\\ =\mbox{Arcsin}y\cdot\frac{a}{1-y^2}-\int\frac{1}{\sqrt{1-y^2}}\cdot\frac{a}{1-y^2}dy$
第二項はθ=Arcsinyと置換すれば、
$\int\frac{a}{\cos^2\theta}d\thta=a\tan\theta+A=\frac{ay}{\sqrt{1-y^2}}$
これを先の式に代入すれば、次のようになる。
$\\\frac{a}{1-y^2}\mbox{Arcsin}y-\frac{ay}{\sqrt{1-y^2}}+A\\ =(x+a)\mbox{Arcsin}\sqrt{\frac{x}{x+a}}-\sqrt{ax}+A\\$

(18.26)定積分せよ。a,b＞0。
$\\\mbox{(1)}\int_0^1x\sqrt{1-x}dx=\int_1^0(1-y)\sqrt{y}(-dy)\;\;[y=1-x]\\ =\left[\frac{2}{3}y\sqrt{y}-\frac{2}{5}y^2\sqrt{y}\right]_0^1=\frac{4}{15}$
$\\\mbox{(2)}\int_0^1\mbox{Arcsin}xdx=\int_0^{\pi/2}\!y\cos ydy\;\;[y=\mbox{Arcsin}x]\\ =[y\sin y]_0^{\pi/2}-\int_0^{\pi/2}\!\sin ydy=\frac{\pi}{2}-1$
$\\\mbox{(3)}\int_0^1\mbox{Arctan}\sqrt{x}dx=\int_0^{\pi/4}\!y\frac{dx}{dy}dy\;\;[y=\mbox{Arctan}\sqrt{x}]\\ =[yx]_0^{\pi/4}-\int_0^{\pi/4}\!xdy=\frac{\pi}{4}-\int_0^{\pi/4}\!\tan^2ydy\\ =\frac{\pi}{4}-\int_0^{\pi/4}\!t^2\left(\frac{1}{\cos^2y}-1\right)dy\\ =\frac{\pi}{4}-[\tan y-y]_0^{\pi/4}=\frac{\pi}{2}-1$
$\\\mbox{(4)}\int_0^{2\pi}\!\frac{1}{a^2\cos^2x+b^2\sin^2x}dx$
とりあえず積分区間を無視してt=tanxが定義される区間で不定積分する。
$\\\int\frac{1}{a^2\cos^2x+b^2\sin^2x}dx\\ =\int\frac{1}{a^2\frac{1}{1+t^2}+b\frac{t^2}{1+t^2}}\cdot\frac{1}{1+t^2}dt\\ =\int\frac{1}{a^2+b^2t^2}dt=\frac{1}{ab}\mbox{Arctan}\frac{bt}{a}+A=F(t)\\$
後は元の積分区間をπ/2,3π/2で分割してそれぞれ求めて合計する:
$\\\mbox{[}F(t)]^{\infty}_0+[F(t)]_{-\infty}^{\infty}+[F(t)]_{-\infty}^0$
あるいは対称性に注目して0からπ/2までの定積分を4倍する:
$4[F(t)]^{\infty}_0=4(\frac{1}{ab}\frac{\pi}{2}-0)=\frac{2\pi}{ab}$
$\\\mbox{(5)}\int_0^{\pi/2}\!\frac{1}{1+\sin x+\cos x}dx\;\;[t=tan\frac{x}{2}]\\ =\int^1_0\frac{1}{1+\frac{2t}{1+t^2}+\frac{1-t^2}{1+t^2}}\frac{2}{1+t^2}dt =\int^1_0\frac{1}{1+t}dt=[\log(1+t)]^1_0=\log 2\\$
$\\\mbox{(6)}\int_0^{\pi}\!\frac{\sin x\cos x}{\sin^4x+\cos^4x}dx$
0からπ/2までの定積分とπ/2からπまでの定積分が打ち消し合って0になる。
[例えば後者の積分でπ-x=yと置換すれば前者の符号を変えたものに等しいと分かる]

(18.27)a<b, α<β, gは[α, β]上で非負, 有界, 積分可能。
$G(t)=a+\int^t_\alpha g(s)ds$ と定め、G(β)=bであるとする。
fは[a,b]上の有界実数値関数。
fが[a,b]上積分可能であるならば、f(G(t))g(t)も[α,β]上積分可能であって、
$\int_a^bf(x)dx=\int_{\alpha}^\beta f(G(t))g(t)dt$
が成り立つことを示せ。

加法的区間関数の性質を用いる方法に従う。
a≦c＜d≦bであるc,dに対して、Φ₁,Φ₂を、
$\Phi_1([c,d])=\underline\int_\xi^\eta(f\circ G)g,\; \Phi_2([c,d])=\overline\int_\xi^\eta(f\circ G)g$
と定める。ただしξ,ηはG(ξ)=c,G(η)=dを満たす[α,β]の元。
[ $\vartheta([a,b])$ (つまり[a,b]に含まれる閉区間全体)から実数への写像]
まず、上の定義がξ,ηによらないことを確かめる:
　ξのみ確かめれば十分。Gはその定義とg≧0により広義単調増加である。
　従ってG(ξ)=cとなるξがただ1つでないとき、その集合は区間であり、
　その区間ではgは0である。従ってどのξを採用しても上の定積分の値は等しい。
次に、これらの写像は加法的区間関数であって、次の条件(*)を満たすことを導く:
(*) $^\forall I\in\vartheta([a,b]);\;\inf f(I)\;|I|\leq \Phi(I)\leq\sup f(I)\;|I|$
[Iは[a,b]に含まれる区間だが、積分区間は[α,β]に含まれる区間である]
　Φ₁だけ考えればΦ₂も同様だろう。
　まずΦ₁([c,d])+Φ₁([d,e])=Φ₁([c,e])を確かめる。
　これはG(ξ)=c,G(η₁)=G(η₂)=d,G(λ)=eとなるξ,η,λを使って、
　 $\underline\int_\xi^{\eta_1}(f\circ G)g+\underline\int^\lambda_{\eta_2}(f\circ G)g =\underline\int_\xi^\lambda(f\circ G)g$ と書かれる。
　先の考察によりη₁,η₂の間でg=0なので等式が示される。
　次に、Gが単調増加なので $G([\xi,\eta])=[c,d]$ であること、及び、
　 $|[c,d]|=d-c=G(\eta)-G(\xi)＝\int_\xi^\eta g$ に注意すると、
　 $\Phi_1([c,d])=\underline\int_\xi^\eta(f\circ G)g\left(\begin{array}{l} \geq\underline\int_\xi^\eta\inf(f\circ G)([\xi,\eta])\;g=\inf f([c,d])|[c,d]|\\ \leq\underline\int_\xi^\eta\sup(f\circ G)([\xi,\eta])\;g=\sup f([c,d])|[c,d]|\end{array}\right)$
さて、Φ₁、Φ₂が(*)を満たす加法的区間関数であることが示された。
"fが[a,b]上積分可能である必要十分条件は、(*)を満たす加法的区間関数Φが一意的に存在することである"
らしいので、これでΦ₁＝Φ₂、従ってf(G(t))g(t)が積分可能であることが示された。

2009/11/7
2010/12/17 数式がいくつかおかしかったので修正

戻る