練習問題15の問題用紙
2/10 問題12.3訂正
残り
問題12.1
被積分関数はxについて積分できない。
そこで、yについて先に積分するのが有効である。
領域0≦y≦√π/2, x≦y≦√π/2 を
領域0≦x≦√π/2, 0≦y≦x と書き換える。
先にyの積分をすると下の積分となってこれは計算できる。
∫xcos(x^2)dx=[sinx^2/2]=1/2.
問題12.2
被積分関数の積分及び領域は、極座標で扱うのが有効そうだ。
そのとき、dxdy=rdrdθとなる。[微小面積はrに比例して]
従って積分は∬r^2drdθとなる。
(1)領域は半円であり、0≦r≦1,-π/2≦θ≦π/2と書ける。
従って∫dθ∫r^2dr=π/3.
(2)x=rcosθを使ってr>0に注意して領域を書き換える。
0≦rcosθ≦r^4≦1
0≦cosθ, cosθ≦r^3, r≦1
-π/2≦θ≦π/2, (cosθ)^1/3≦r≦1
∫[r^3/3]dθ=∫(1-cosθ)/3 dθ=(π-2)/3.
(3)これは(1)と(2)を合わせた領域である。
従って2つの領域の積分値を合計して2(π-1)/3.
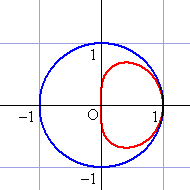
参考にx=x^2+y^2のグラフを画像の赤線で示した。
赤と青の間の領域が(3)の領域に相当する。
問題12.3
重積分で座標変換する時に書き換える場所は3つある。
1.被積分関数は √(1-r^2)
2.積分領域は 0≦r≦1, 0≦θ≦π, 0≦φ≦2π
3.dxdydzのところ。これを忘れないようにする。
偏微分したものを並べたヤコビ行列の行列式を計算すると得られる。
...このような球面座標ではdxdydz=r^2sinθdrdθdφとなる。
積分は∫r^2√(1-r^2)dr ∫sinθdθ ∫dφとなる
rについての積分は適当に置換積分するしかなさそう。
π/8っぽい。後は順に2,2πであるので、合わせてπ^2/2.
π/16でした。従って答えはπ^2/4でした。
問題13.1
(1)Qを(cosθ,sinθ)とおくと、Sは扇形の面積でS=θ/2だから、
θ=2Sであり、Qの座標は(cos2S,sin2S)と書ける。
(2)極座標を使うと煩雑になる。そのかわりにQの座標を、
(x,√x^2-1)あるいは(√y^2+1,y)のようにおくと、
∫√y^2+1 dyのような積分ができれば大変ではない。
S=log(x+y)/2のようなものを得るはずである。逆に解くと、
x=(e^2S-e^-2S)/2, y=(e^2S-e^-2S)/2.
答えの形の通り、双曲線関数を使うのは有効である。
[x=rcoshθ=r(e^θ-e^-θ)/2, y=rsinhθ=r(e^θ-e^-θ)/2]
双曲線はr=1で表される。Qがθの位置の面積Sを計算する。
領域は0≦r≦1, 0≦θ≦θ, またdxdy=rdrdθ,
S=∬rdrdθ=∫1/2dθ=θ/2, θ=2Sであり, Q:(cosh2S,sinh2S)
問題13.2
例によって曲線を示しておく。
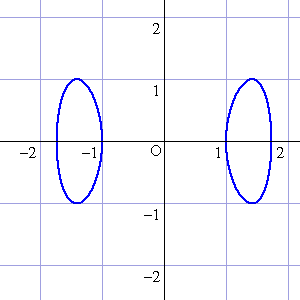
回転体の体積を求める方法はとりあえず3つくらいある。
1.軸に垂直な円盤の面積を、回転軸の方向に積分する
2.円筒の表面積を、回転軸に離れる向きに積分する
3.重心の位置と断面積を計算して、 某定理を使う
今回は1と2の両方が有効のように見える。
[1の方法]
この方法ではy=yでの断面に注目する。つまり方程式をxについて解く。
x=±√(2±√1-y^2)となる。
断面は5円玉状で、外側の半径が√(2+√1-y^2)、内側が√(2-√1-y^2)、
従ってその面積を計算すると...2π√1-y^2となる。
これをyについて-1から1まで積分すると求める体積π^2を得る。
(この積分範囲はyについて解いた式から把握することができる)
[2の方法]
こちらでは方程式をyについて解く。y=±√{1-(x^2-2)^2}となる。
円筒は半径がxで(従って円周は2πx)、長さが2√{1-(x^2-2)^2}、
従って表面積は4πx√{1-(x^2-2)^2}となる。
これをxについて1から√3まで積分すると求める体積を得る。
(この積分範囲もyについて解いた式から把握することができる)
この積分はx^2-2=kのように置換積分すると1の方法のと同じ式になる。
問題13.3
xy平面上のx^2+y^2≦b^2の領域で、球の高さ√a^2-x^2-y^2を重積分する。
計算は極座標を使うのが良いだろう。
∬√(a^2-r^2) rdrdθ [0≦r≦b, 0≦θ≦2π]
=2π[-1/3 (a^2-r^2)^(3/2)]
=2π/3 {a^3 - (a^2-b^2)^(3/2)}
これがxy平面よりも上の部分の体積に相当するので、2倍する。
4π/3 {a^3 - (a^2-b^2)^(3/2)}
[a=bの時に球の体積に一致する]
問題13.4
重心を求めるには、"位置ベクトル"(座標)を重積分して面積で割る。
(いくつか質点があったときの重心の式を思い出して)
それに従って計算する。領域は0≦x≦1, x^2≦y≦x と書かれる。
∬(x,y)dxdy
=∫([xy],[y^2/2])dx
=∫(x(x-x^2),(x^2-x^4)/2)dx
=(1/3-1/4,(1/3-1/5)/2)
=(1/12,1/15)
これを忘れずに領域の面積で割る。
[∬dxdy=∫(x-x^2)dx=1/6]
求める重心は(1/2,2/5)である。
問題13.5
tからdtの変位で点が動く長さを計算して積分すればよい。
すなわち∫√{(dx/dt)^2+(dy/dt)^2}dtを計算すればよい。
∫√(4t^2+9t^4)dt
=∫|t|√(4+9t^2)dt
(0≦t≦1の部分を計算して2倍することにする)
=2*[1/27 (4+9t^2)^(3/2)]
=2(13√13-8)/27.
問題15.1
(1) 1/1+x=1-x+x^2-x^3+...を項別積分する
(2) 1/1+x^2=1-x^2+x^4-...を項別積分する
問題15.2
f(x)=(1+x)^αをそれに適用すればいいと思う(a=0)
|x|<1 に注意して、"残りの部分"が0に収束することを確かめる。
問題15.3
F(x,y,t)というものをよく見ると、これは、
t=0のときf(a,b), t=1のときf(x,y)である。
そこで、Fをtについて微分すると、
∂F(x,y,t)/∂t=(x-a)∂f(ry)/∂x+(y-b)∂f(ry)/∂y
これをtについて0から1まで定積分すれば、
f(x,y)-f(a,b)=(x-a)∫∂f(ry)/∂xdt+(y-b)∫∂f(ry)/∂y
ということは、[f(ry)をちゃんと書いて]
g(x,y)=∫∂f(a+(x-a)t,b+(y-b)t)/∂x dt
h(x,y)=∫∂f(a+(x-a)t,b+(y-b)t)/∂y dt
とすればよい。連続関数のはず。
問題15.4
(1)∫(1-t^2)^(n/2)dt=[t(1-t^2)^(n/2)]-∫t{(1-t^2)^(n/2)}'dt
と部分積分をする。あとはt=1-(1-t)のようにみなして..
I[n]=n(I[n-2]-I[n]) すなわち I[n]=n/n+1 I[n-2]
(2)相似を利用する、すなわちV[k](r)=V[k](1)*r^kを使う。
V[n](1)=∫V[n-1](√1-r^2)dr
=V[n-1](1)*∫{√(1-r^2)}^(n-1)dr
=V[n-1](1)I[n-1]
(3)V[1](1)=2,V[2](1)=πを種にしてI[k]をかければそうなりそう
2010/2/3