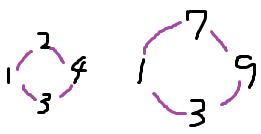合成数一般の時

法が合成数一般の時、原始根が存在する条件は以下の通りである。

原始根が存在する時：
　p＝2,4,奇素数,奇素数のべき乗,2*奇素数,2*(奇素数のべき乗)
原始根が存在しない時：
　p＝4以外の4の倍数,異なる奇素数で割り切れる数

・奇素数のべき乗については前節を参照。
・p=8の時は前節の例外であった。既約剰余類{1,3,5,7}について、
　3,5,7はいずれも2乗で1になるから巡回網羅することが不可能である。
・p=16,32,...の時も、8N+3型のべき乗は8N+7型になれないし、逆も真なので巡回不可能。

・pが互いに素な数P,Qの積の時は下記で考察する。

・p=15ではpと素なxは{1,2,4,7,8,11,13,14}の8個。
　5で割った余りaと3で割った余りbに注目すると次のようになる。

b; a:	1	2	3	4
1	1	7	13	4
2	11	2	8	14

xを5で割った余りがa, 3で割った余りがbとすると
x^kを5で割った余り≡a^k, 3で割った余り≡b^kとなる。
∵(5N+a)^k≡a^k (mod 5), (3N+b)^k≡b^k (mod 3)

従ってp=15のx^k図は、p=3の図(左上)とp=5の図(左下)を合体させたものである。

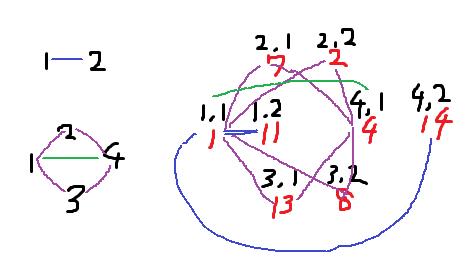
＃図より、11,4,14は2乗すると1になり、7,2,13,8は4乗すると1になる。
＃ということはx^kが8個の数字を巡回網羅するxは存在しない。
＃それもそのはず、5で割った余りは4乗で1になるし、3で割った余りは2乗で1になる。
　だから、15で割った余りは4乗ですでに1になってしまうはず。

P,Qを互いに素とする。(mod PQ)におけるx^kの値を考える。
x^kをPで割った余りはk=φ(P)で1になる。
x^kをQで割った余りはk=φ(Q)で1になる。
よってx^kをPQで割った余りはk=(φ(P)とφ(Q)の最小公倍数)で1になる。
・φ(P)とφ(Q)が共に偶数ならば、それらの最小公倍数は積φ(P)φ(Q)より小さくなる。
その場合PQと素な剰余類はφ(PQ)＝φ(P)φ(Q)個あるから巡回網羅できなくなる。
・実はp≧3のときφ(p)は偶数になることが確認できる。
　従って原始根を持つとしたらP,Qのどちらかが2である。
・逆に、Pが奇数で(mod P)が原始根を持つなら(mod 2P)も原始根を持つ。
　mod Pの原始根をaとして、Pで割ってa余る奇数をとれば良い。

＃例：p=10では次のようになる

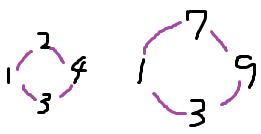
3と7はべき乗が4つの既約剰余類を巡回網羅、つまり原始根であることが分かる。