[1] きっかけ、楕円曲線の結合法則 [2] パスカルの円錐曲線試論との再会、射影幾何 [3] アポロニウスの円錐曲線論との出会い [4] 日曜数学会で話すつもりの内容 [5] 追記 [1][2]では脱線と称して、それぞれ 楕円曲線の3点の加法A+B+Cを放物線を使って認識する視点の説明 射影平面の、射影的な視点で捉える方法と、他の視点との関係の説明 を書きました。 どちらも「そういうことだったのか」と私がとても腑に落ちた内容です。
[1] 楕円曲線の加法演算の結合法則について考える機会がありました。 （素数大富豪オンラインでなぜか話題になりました。） 色々な視点があるのですが、初等的にはwikipediaにあるように、 「加法の結合律は、(3つの直線がなす)格子の中心点を楕円曲線が通るという事実と同値である。」 という視点が１つあって、これを説明するには、以前に https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14144947309 で出会った交点定理： 「2つのn次射影曲線(f=0,g=0)がn^2個の交点を持ち、 そのうちのnr個がr次曲線上に存在するならば、 残りのn(n-r)個の点は(n-r)次曲線上にある」 が使えます。 （fとして楕円曲線の方程式、gとして図の赤の3つの直線の方程式の積を適用すれば良い。 fとgのなす9個の交点のうち、6個は2直線＝2次曲線上に存在するので、 交点定理のn=3,r=2の場合により、残り3個の点は1次曲線＝直線上に存在する。）
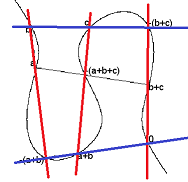この交点定理は、通常ベズーの定理を経由して証明されるようで
それについては次の現代的な資料を見つけました：
http://www.kurims.kyoto-u.ac.jp/~kenkyubu/kokai-koza/H30-mukai.pdf
一番最後に、ベズーの定理の証明が簡略にあります。高度な内容です。
# 脱線
思いついたもう1つの視点（因子類群の視点と深く関係する）を紹介します：
・A+B+C+D=0 ⇔ A,B,C,Dの4点で楕円曲線と交わる2次曲線が存在する
・A,B,Cのx座標はすべて異なるとする。
A,B,Cを通る放物線y=px^2+qx+rがただ1つ存在する。
それを y^2 = x^3+ax^2+bx+c と連立させると、4つの解が存在する。
それがA+B+C+D=0となるような点Dである
具体的には以下のようにして（特殊な場合を除いて）結合法則を説明することができました。
[考察]
以下の事実を示す：
（ただし単純のため、A,B,(A+B),C,Dのx座標が重複していない場合に限定する。）
「（古典的な意味での）(A+B),C,D が一直線上となるように設定する。
このとき、A,B,C,Dの4点で楕円曲線と交わる放物線が存在する。」
この事実が示せれば、A,B,Cを通る放物線は一意的であることと、、
例えば(B+C),A,Dが一直線上になるような点Dも同じ性質を満たすことから、
(A+B)+C と (B+C)+A が同じ点であることが納得される。
この事実も、また交点定理を使って示せるが、
交点定理を使わなくても、次にように地に足がついた視点で説明できた。
楕円曲線をy^2=x^3+ax^2+bx+cとおく。
A,B,Pを通る直線を y=p(x-t)+q, P',C,Dを通る直線を y=r(x-t)-q とおく。
ここで、PとP'はx座標が等しく、それがx=tであるとおいた。
すなわちこの点P'を古典的な意味でのA+Bと設定している。
F(x,y) = (p(x-t)+q-y)(r(x-t)-q-y) + (x^3+ax^2+bx+c-y^2) とおく。
ここで楕円曲線は、直線x=tとy=±qで交わることから、
(x^3+ax^2+bx+c-y^2) = (x-t)(xの2次式)-(y^2-q^2) とおける。
F(x,y)は (x-t)を因数にもち、F(x,y)=(x-t)*G(x,y)とおける。
次数の観察により、G(x,y)は (定数)*y + (xの2次式) の形と分かる。
点A,B,C,Dでは(x-t)は0にならないが、F(x,y)は0になるから、G(x,y)が0にならなくてはいけない。
すなわち放物線G(x,y)=0 はA,B,C,Dを通る。
# もう1つどうしても書かずにいられない（知らないともったいない）のは複素トーラスの視点です。
楕円曲線E上の(複素数)点は、ある複素トーラスC/Λ上の複素数と対応します。
(http://tsujimotter.hatenablog.com/entry/complex-multiplication-2)
楕円曲線E上の点A,Bに対応するC/Λの点をzA,zBとすると、
楕円曲線E上の点A+Bは、C/Λの点zA+zBに相当します。（通常の複素数の加法で誘導された演算）
[2] 上記Yahoo知恵袋質問で言及のあるパスカルの定理というのを思い出して周辺を調べると、 青空学園の「幾何学の精神」というページに再会しました： http://aozoragakuen.sakura.ne.jp/pascal/pascal.html このページはタイトルに負けない深い内容で、 パスカルの「円錐曲線試論」の翻訳・解説だけでなく、 改めて射影幾何を公理的に構成しようという試みも含んだ壮大なページです。 円錐曲線試論は、いくつかの定義、3つの命題、5つの系が書かれています。 1つ目の命題が、円の場合のパスカルの定理であり、 2つ目の命題が「射影」の手法に関わるもので、 3つ目の命題が、一般の円錐曲線の場合のパスカルの定理な内容です。 そしてその最後の段落が印象的すぎるので引用紹介します： 「以上の他にも多くの問題や定理，またそこから導かれる多くの結論を得ている． しかし私は経験も浅く能力も乏しいので，先学が検討の労をとって下さるまで， この先に進むことは控えたい．検討された後，続ける意義があると認められたなら， 神がことを運ぶ力を与えたまうかぎり，研究を推し進めるつもりである．」 ところで、「幾何学の精神」という言葉はパスカルの言葉でもあり、次のような文脈らしいです： 人間には2つの精神があって、どちらも大事である： ・日常生活の様々な事柄を微妙な心情の動きに基づいて情感的かつ繊細に感じ取り自らを高めていく「繊細の精神」 ・一切の事柄を定義し理論立てていく「幾何学的精神」 (参考：「パンセを読む」第一章の1ページ目) #脱線 射影平面は、いろんな方法で描写される。 ・平面に無限遠点を付け加えたもの（便宜的な視点） ・斉次座標：「3つの数の比」[x:y:z]（代数的な視点） ・任意の異なる2直線は1点で交わる（公理的な視点） ・ここでは射影される点を同一視するという視点を紹介したい。（射影的な視点・貼り合わせの視点） 上記の視点たちとの結びつきも説明する。 ・射影
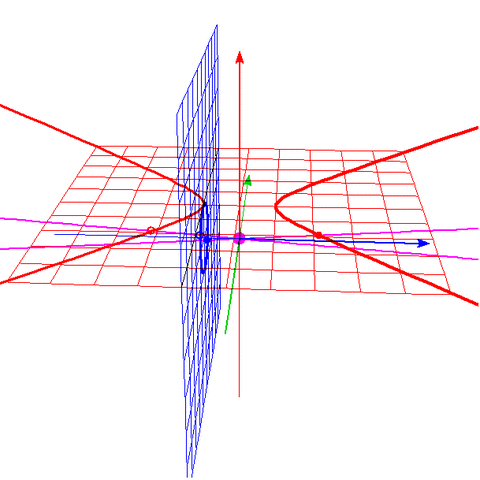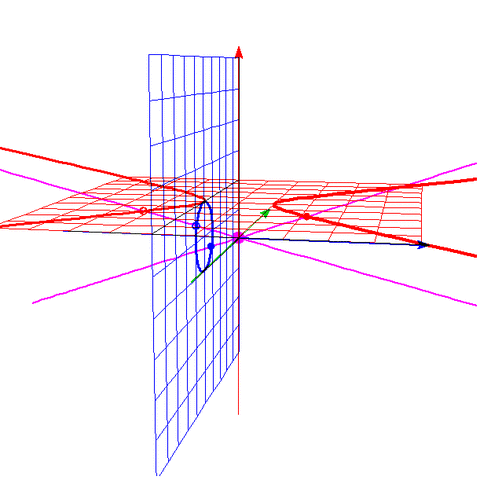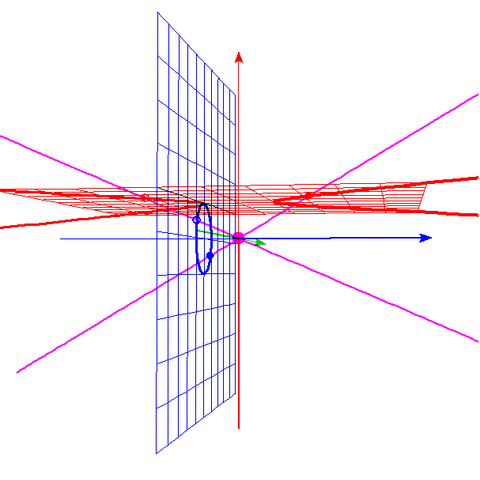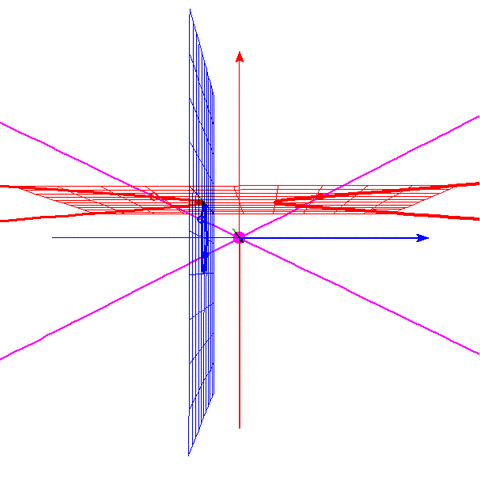これは3D-GRAPESで描いて ウェブツールでGIF動画に変換したものである。
青がx軸、緑がy軸、赤がz軸、赤の平面がz=1、青の平面がx=-1、紫が原点。
平面z=1上の赤い曲線（双曲線）上に点aをとる。
点aと原点を結ぶ紫の直線を描く。
それと青の平面との交点を点bとする。
この操作を、(原点による、赤い平面から青い平面への)「射影」と呼ぶ。
点aが赤い曲線（双曲線）上を動いていくと、点bが青い曲線（円）上を動く様子である。
・無限遠点
青い平面上の、z=0、つまり{(-1,y,0)}という直線上の点は、赤い平面に射影されない。
円周上の点では、2点(-1,±1,0)は、赤い平面上の点に対応しない。
これは、これらの点と原点を結ぶ直線が、赤い平面に平行になってしまうからである。
2つの漸近線を無限円に伸ばしていった方向の無限遠点として考えたいが、一旦保留する。
・射影的な視点
上記の射影を概念を活かした定義を考えた：
{(α,p)|αは原点を通らない平面、pはその平面上の点}という集合を、
射影で移りあう点を同値とみなした同値関係で割った集合が、射影平面である。
（この説明は、分からなくても気にしなくて良い。）
もう少し、平易な説明を試みる。
・射影平面は、その全体を、同時に「眺める」ことはできない。
・視点を固定して眺めると、それは通常の平面のような形をしている。（赤の平面）
・他の視点から眺めたときも、通常の平面のような形をしている。（青の平面）
・2つの視点から眺めたときの、同一性は、上記の射影で結びつける。
例えば赤の視点で眺めた時の点(1,0,1)は、青の視点で眺めた時の点(-1,0,-1)に対応する。
・ここで赤の視点では見えない点が存在する；赤の視点では射影平面の全体を眺められていない：
具体的には青の視点で(-1,y,0)に見える点は、赤の視点では見えない。
・全体を眺めるには少なくとも3つの視点を組み合わせる必要がある。
（問題：赤の視点でも青の視点でも見えない点はどのような点か？）
・こうして組み合わせた全体像が「射影平面」である
他の視点との関係
・よく考えると射影平面上の点は、「原点を通る(紫の)直線」と1対1に対応することが分かる。
この直線の方向ベクトルを取り出せば、斉次座標の視点に結びつく。
・赤の視点では見えない点は、原点を通る直線の言葉では、xy平面に含まれてしまうものに対応する。
これが、便宜的に、赤の平面の、該当する方向の無限遠点として捉えられる。
・赤の視点での平行線は、別の視点では、X字をなす。
Xの交点は赤の平面上では見えない点である。
これが、平行線が(便宜的な無限遠点で)交わる様子である。
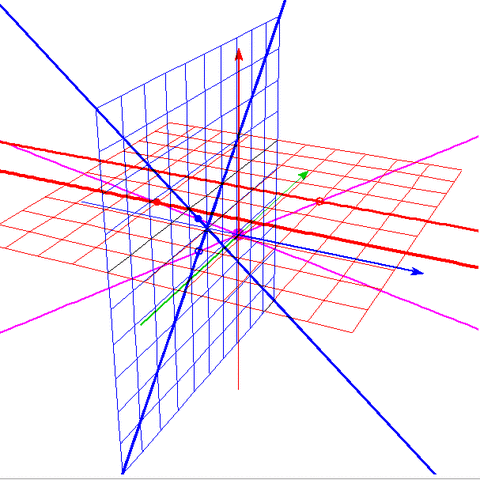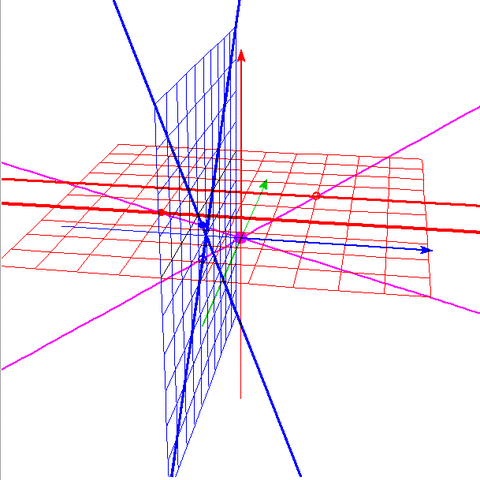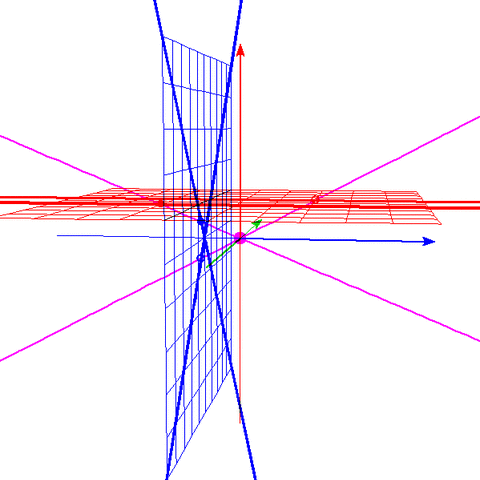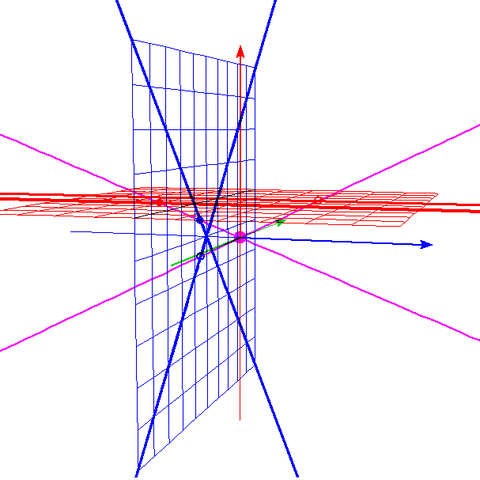・青の視点で円に見える曲線を、赤の視点で見ると双曲線に見えるという様子は、
ちょうど青の円と原点を結んだ円錐を、赤の平面で切断するのと同等である。
・すなわち、射影平面のうち、ある視点で円周上に見える点（射影曲線としての円錐曲線）を、
いろんな視点で見た結果が、（平面曲線としての）円錐曲線である、と言える。
・斉次座標を使った代数的な視点では、射影曲線としての円錐曲線は次のように描写される。
「x^2=y^2+z^2 を満たす (x,y,z)を方向ベクトルとするような原点から出発する直線の集まり」
例えばz=1とおく(非斉次化)と、z=1という平面への射影を考える赤の視点に帰着する。
[3] さて「幾何学の精神」を読んでいる中で、その「本文読解」というページに、 題材：アポロニウスの「円錐曲線論」（というウェブページ）の紹介がありました。 「訳とそのすべてに図を与える労作である」と紹介されています。 これが私のアポロニウスの「円錐曲線論」との出会いです。 ところがその図は、ほとんどJava appletを要求するものでした。 時代の変化により私の環境で閲覧することはできませんでした。 文字だけで解読しようと試みましたが、用語が独特で、解読は困難でした。 せっかくなのでGoogle検索すると ・同じウェブサイト内の数学史教育の授業テキスト ・それとは全く別な「アポロニウスの円錐曲線論」という内容のpdfファイル に出会いました。 このテキストを読むと用語の説明もいくらかあり、先のページの解読が少ししやすくなりました。 また、そのテキストが含まれる数学史トップへ戻ってみると、 古代数学的な話題がたくさんあります。いくつか適当に眺めましたが、なかなか興味深いです。 （ただし資料は授業テキスト的な形で公開されているので行間を埋めながら読む必要がありそうです。） 別のほうのpdfファイルには、円錐曲線の焦点に関する鮮やかな証明が紹介されています。 ただし、これが「アポロニウスの円錐曲線論」に記述されたものであることは確認できていないです。 （pdfのタイトルなどからおそらくそうだと推測しています。）
[4] 日曜数学会では： ・命題11を題材にして、雰囲気を伝えたい （その記述のまわりくどさを感じつつ、内容を解説する） ・解読のために必要な「直径」「縦線方向」という独特の用語の意味を紹介する （使用例として、命題20を軽く紹介する） ・pdfファイルの鮮やかな証明は、若干行間の補足があると良いと思うのでそれを説明したい つもりです。（今の所です。気が変わるかもしれません。）