2018年4月の疑問： https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14189711909 複素射影平面P^2上のd次非特異代数曲線Cをとりその補集合Xを考えると Xの基本群π_1(X)はZ/dZになるらしいです それって私の認識だと、ある閉曲線があって、 「閉曲線に沿って糸をd周通すとほどける」 ということだと思うのですが、イメージできないです・・ ---- これに対する1つの描写を見つけた。 ---- 3次曲線: X^3+Y^3=Z^3 を考える。 主にアフィンU : [x:y:1], x^3+y^3=1で考える。
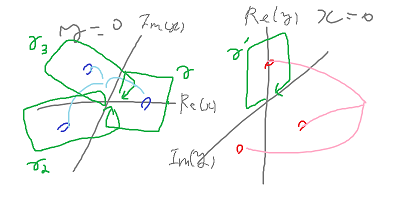断面y=0でのCの点(x,y)=(1,0)を囲むようなXのループγを考える。
(x,y)=(i,0), (2+i,0), (2-i,0), (-i,0)を正方形につないだ。
以下の4つの線分で記述される：
P1: (it,0) [t=-1..1]
P2: (t+i,0) [t=0..2]
P3: (2-it,0) [t=-1..1]
P4: (2-t-i,0) [t=0..2]
同様にxとyを入れ替えてできる断面x=0でのループγ'を考える。
以下の4つの線分で記述される：
R1: (0,it) [t=-1..1]
R2: (0,t+i) [t=0..2]
R3: (0,2-it) [t=-1..1]
R4: (0,2-t-i) [t=0..2]
γとγ'はホモトピー同値であることを確認した。[s=0..1]
Q1: (it(1-s),its) [t=-1..1]
Q2: ((t+i)(1-s),(t+i)s) [t=0..2]
Q3: ((2-it)(1-s),(2-it)s) [t=-1..1]
Q4: ((2-t-i)(1-s),(2-t-i)s) [t=0..2]
これが実際にXにおけるホモトピーであることのために、
s,tが実数の範囲ではCと交わらないことを確認した。
[x^3+y^3の実部=虚部=0とおくと3s^2-3s+1=0で実数解がない]
これらのx座標に(-1±i√3)/2を掛ければ、
(x,y)=((-1±i√3)/2,0)を囲むループγ_2,γ_3もγ'にホモトピー同値である。
[x^3は変わらないので、ホモトピーの確認の計算は同じ計算である。]
そこで、図のようにγ,γ_2,γ_3をつなげると、
3点(x,y)=(1,0),((-1±i√3)/2,0)を囲むループができて、
これは無限遠点[X:Y:Z]=[1:0:0]をCと交わらずに結べるから可縮である。
そういうわけで、γは基本群の元として、3γ=0を満たす。
（ただしXの基本群がZ/3Zであることを示すにはさらに、
基本群がγだけで生成され、γ≠0であることを示す必要がある。）
2020/10/24