3^n+13 = m^2 の場合を例に具体的に紹介する。これは https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13154454723 で出会い、この「証人探し法」を編み出すきっかけになった問題である(2016/1/9) [1] nが偶数の場合は3^(n/2)=xとおくと(x-m)(x+m)=-13として考察できて 素因数分解的考察からx=±7,m=±6を得るがx=3^(n/2)の形でないので不適 [2] nが奇数の場合を考える。x^2-3y^2=13 を考える。 次の数列が、yを網羅的に与える。 y[0]=1, y[1]=6, y[k+2]=4*y[k+1]-y[k] 一般項を記述すると y[k] = {(4+√3)(2+√3)^k-(4-√3)(2-√3)^k} / 2√3 状況を正確に説明すると：「任意の整数解(x,y)に対して y=y[k]またはy=-y[k] となる(負かもしれない)整数kが存在する」 今回の場合はy[0]=1, y[-2]=-9 がy[k]=±3^nの形を与える。 これら以外にないことを示すのが目標である。 [3] y[k]が3^qで割り切れるようなkは次のような挙動をする： y[k]は3で割り切れる ⇔ k≡1 (mod 3) y[k]は3^2 で割り切れる ⇔ k≡7 (mod 3^2) y[k]は3^3 で割り切れる ⇔ k≡7 (mod 3^3) y[k]は3^4 で割り切れる ⇔ k≡7 (mod 3^4) y[k]は3^5 で割り切れる ⇔ k≡7+2*3^4=169 (mod 3^5) y[k]は3^6 で割り切れる ⇔ k≡7+2*3^4+2*3^5=655 (mod 3^6)・・・ [4] とても唐突であるがp=56377が今回の問題に対する良い証人となる。 y[k]をpで割った余りは周期3^5を持つ。 k≡7+2*3^4 (mod 3^5) のとき、y[k]をpで割った余りは37330となる。 [3]と合わせると、次の状況である： 「y[k]が3^5で割り切れる時、それをpで割った余りは常に37330になる」 一方で、3の冪乗をpで割った余りは、56376個の既約剰余類のうち7047個だけを巡回する。 そしてめでたいことに、37330はその巡回に入っていない。 従って、y[k]が3^5で割り切れてかつy[k]が3の冪乗であるようなkは存在しない。 さらにめでたいことに、-37330≡19047もその巡回に入っていない。 従って、y[k]が3^5で割り切れてかつ-y[k]が3の冪乗であるようなkも存在しない。 あとはy=3,3^3,3^4のとき x^2-3y^2=13 となるxが整数でないことを確認すれば、 y=1,9が求めるものすべてであることが示された。 ＊現象を先に描写して、詳細を補足する形をとっている。 実際に現象を観察するためのヒントとしては、 上記の形の数列y[k]を適当な法pで割った余りが周期Nを持つことを確認するには、 y[0]≡y[N],y[1]≡y[N+1] (mod p) を計算機で確認すれば十分である。 なぜなら整数係数3項間漸化式の関係式があるからである
[2]に関する2次体の整数論について補足する。 x^2-3y^2=13 となるx,yの一般解を描写する。 Q(√3)の整数環と呼ばれるものに一致する集合 A={a+b√3|a,b∈Z} を考える。 Aの元を表すのにα,βなどを使うことにする。 (a+b√3)/(c+d√3)∈Aのとき、(a+b√3)は(c+d√3)で割り切れると呼ぶ 状況として、3N+1型素数pに対しては p=a^2-3b^2=(a+b√3)(a-b√3)となる背う数a,bが存在することから話を始める。 p=13 の場合は例えば 13=(4+√3)(4-√3) である。 ・まず次が成り立つ： [命題] a^2-3b^2が13で割り切れるならば、(a+b√3)は(4+√3)または(4-√3)で割り切れる これは、(4+√3)が素元であるということによる。つまり： α,β∈Aに対してαβが(4+√3)で割り切れるならばα,βのどちらかが(4+√3)で割り切れる これは、代数学の言葉を使えば次のように納得できる： 「(4+√3)で割った「余り」は13種類で素数だから、剰余環A/(4+√3)が必然的に整域（あるいは体）となるから」 そういうわけで(a+b√3)(a-b√3)が13で割り切れるならば (a+b√3),(a-b√3)のどちらかは(4+√3)で割り切れて、これから命題が従う。 そういうわけで、 a^2-3b^2=13ならば、(a+b√3)=(4+√3)α,(a-b√3)=(4-√3)β [α,β∈A] とおける αβ=1 である。逆にこのようなα,β∈Aが a^2-3b^2=13となるa,bを与える。 α,1/αがともにAに属するαを探すことになる。このようなαは「単数」と呼ばれる ・次に、単数に関する命題である： 「環Aの単数は、次の形ですべてである：α=±(2+√3)^k [kは整数]」 これは強い視点ではディリクレの単数定理と呼ばれる定理の帰結である。 ディリクレの単数定理まで訴えないで、しかしある程度一般的な視点で説明してみる。 α=a+b√3に対して、(x,y)=(a,b)を対応させる。 双曲線x^2-3y^2=1を描く。この上にある整数点が単数に対応する。 漸近線をなすベクトル(√3,-1)をX軸、ベクトル(√3,1)をY軸と設定しておく。 x,yが正の範囲でyが最小となるような整数点(x0,y0)をとる。（存在は前提とする） ε=(x0+y0√3)とおく。ε^k [k∈Z] は一連の整数点p[k]を定める。 具体的には、ε=2+√3, (2+√3)^2=7+4√3, (2+√3)^3=26+15√3,...に対応して p[0]=(1,0), p[1]=(2,1), p[2]=(7,4), p[3]=(26,15), ... という一連の整数点が並ぶ。 kを負にすれば、y座標が負の方向に伸びて行く。
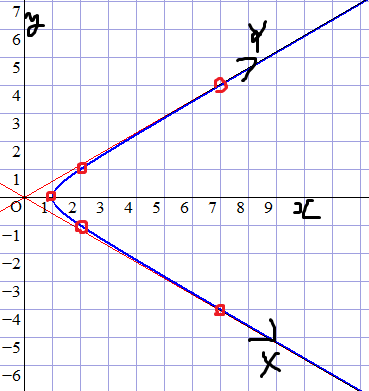ここで、α=a+b√3に対応する点に、ε=2+√3を掛けるという操作は、
X軸方向に1/(2+√3)倍、Y軸方向に(2+√3)倍、という縮小＋引き延ばし操作に相当する。
つまり、曲線x^2-3y^2=1上のp[k-1]とp[k]の間にある点(x,y)に相当するAの元x+y√3に対して、
(x+y√3)(2+√3)=x'+y'√3 に相当する点(x',y')を考えると
同じ曲線のp[k]とp[k+1]の間に存在する、という振舞いがあるのだ。
（そしてx,yが整数ならx',y'も整数である）
（同様に、(x+y√3)/(2+√3)=(x+y√3)(2-√3)=x"+y"√3 をとれば、
点(x",y")はp[k-2]とp[k-1]の間に存在する整数点となる）
そういうわけで、一連のp[k]以外の整数点が存在したと仮定すると、
(2+√3)を整数解掛けることにより、p[0]とp[1]の間に整数点が存在することを要求できる。
それはεの設定にあるyの最小性に矛盾するから、一連のp[k]以外には整数点は存在しないことが言えた。
・今挙げた2つの命題により、
x^2-3y^2=13の形の解は、x+y√3 = ±(2+√3)^n * (4±√3) の形ですべて尽くせる。
複号の選び方によって4つの系列があるが、(x,y)の符号の組み合わせの違いに相当するから
符号を無視すれば1つの系列を考えれば十分である。
そうして、x+y√3 = (2+√3)^k * (4+√3) で得られるyがy[k]と定義した数列であった。
[3]に関する補足 このような挙動はもちろん実際に計算機で調べれば得ることができるが、 背景には局所体の指数対数準同型が関連が深いと思っている。 より初等的な言葉だと、「指数持ち上げの定理」が深く関係する y[k] = {(4+√3)(2+√3)^k-(4-√3)(2-√3)^k} / 2√3 が 3で割り切れる回数に興味がある。 = [{(2+√3)/(2-√3)}^k - (4-√3)/(4+√3)] * (3と互いに素な部分) / √3 の形で考察する。 2次体の整数環で書かれると複雑な状況に見えるかもしれない まずは普通の整数環の言葉で同様のことを考えると仕組みが見えやすいと思う ・例えば y[k] = 7^k-13 が3で割り切れる回数 の挙動について 7^kを3で割った余りは常に1 7^kを9で割った余りは3種類の3N+1型余り(1,4,7)を巡回する 7^kを27で割った余りは9種類の3N+1型余りを巡回する 7^kを81で割った余りは27種類の3N+1型余りを巡回する ... 7^k-13は常に3で割り切れる 7^k-13が9で割り切れる ⇔ k≡2 (mod 3) 7^k-13が27で割り切れる ⇔ k≡5 (mod 9) 7^k-13が81で割り切れる ⇔ k≡14 (mod 27) 7^k-13が243で割り切れる ⇔ k≡？ (mod 81)・・・ と続き、 この？には14,14+27,14+54の3つのどれか1つだけが適するはずである。 それで良いのであるが実はp進logという概念が直接的計算方法を与えて興味深いので紹介する： https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11158473256 2次体の整数環でも同様の現象が成り立つのである。 正確には注意点がいくつかあるが、細かくなるので省略するのである。 ・y[k] = [{(2+√3)/(2-√3)}^k - (4-√3)/(4+√3)] * (3と互いに素な部分) / √3 の形で具体的にp進logの効果を紹介したい。 （「現象の紹介」が主な目的であり、記述は根拠がなく正確でない） f(x):=x-x^2/2+x^3/3-x^4/4+x^5/5-x^6/6+x^7/7-x^8/8+x^9/9-x^10/10+x^11/11-x^12/12 とおく。 これがlog(1+x)の「近似」である。 xが√3で割り切れる時、x^13/13以降の項は3で6回割り切れるという意味で log(1+x)≡f(x) (mod 3^6) f(-3±√3)=(±1518609842√3-2630313648)/385 f(3±√3)=-(±949093396*sqrt(3)+1643877966)/385 形式的に y[k]≡0 を k≡log{(4-√3)/(4+√3)} / log{(2+√3)/(2-√3)} と解いて log{(4-√3)/(4+√3)} ≡ f(3-√3)-f(3+√3) (mod 3^6) log{(2+√3)/(2-√3)} ≡ f(-3-√3)-f(-3+√3) (mod 3^6) で「近似」すると k≡-474546698√3/759304921√3≡655 (mod 3^6) ＊分数の合同式は自然な方法による拡張である ＊正確には√3の約分で(mod 3^5*√3) と退化するが整数の合同式なので3^6の精度が言える この結果は[3]で見た y[k]≡0 (mod 3^6) ⇔ k≡655 (mod 3^6) という結果と合っている。 この辺りが上記の[3]で示したような周期的な挙動をする背景であると思う。 しかし実際な周期的な挙動自体は計算機による探索で得れば良いように思う。
[4]の補足 この手法の一番鍵となり、一番難しい所である。 良い証人を探してくる必要がある。 私は例えばy[k]をpで割った余りが周期3^4を持つようなpを候補として、他の条件を満たすか調べる だめだったら周期3^5で探してみる・・ というふうにして具体的に探していった。 y[k]をpで割った余りが周期3^4=81を持つような法pを挙げる方法について： 直接的には (2+√3)^81 - 1 の約数を挙げれば良い： (2+√3)^81=A+B√3 とおいたときのA-1とBの公約数を探すのである。 現代のコンピュータを使えば有難いことに直接計算でも十分現実的な範囲である。 一方で実はちょっと変法があって、単にBの約数をとれば、 3^4より少し大きくなるが、周期4*3^4を持つような法を得ることができる。 周期が3^4より少し長くても、複数の剰余類が条件を満たすことを確認すれば良いのである 後の例にはそのような例が登場する。（5^n±19=m^2という例） 次の段階に、p=56377に対して 「3の冪乗をpで割った余りが56376個の既約剰余類のうち7047個だけを巡回し、 ±37330はその巡回から外れている」という内容の得かたを紹介する。 ・巡回の長さの求め方 フェルマーの小定理で 3^56376≡1 (mod p) である。 56376=2^3*3^5*29 と素因数分解して 3^(56376/2)≡1, 3^(56376/4)≡1, 3^(56376/8)≡1 3^(56376/3)≠1, 3^(56376/29)≠1 (mod p) と確認すれば、56376/8=7047が3^a≡1 (mod p)となる最小のaだと確定する。 ・他の剰余類が巡回から外れていることの確認 ある剰余類xがその巡回に含まれるかどうかはx^7047≡1 (mod p)となるかどうかで判定できる。 もし x≡3^a ならば x^7047≡(3^a)^7047≡(3^7047)^a≡1^a≡1 (mod p) である。 （【pを素数とする。(Z/pZ)* は巡回群である】という性質により、逆も成り立つ。） 先の例では 37330^7047≡34331 (mod p) なので、37330は巡回に含まれていないと判定できる。 （これは「オイラーの規準」と呼ばれる考え方の一般化である。）
他の具体例 ・（本家の）Ramanujan-Nagell方程式 2^n-7 = m^2 x^2-2y^2=-7 で y=±2^nとなる解を探すことに帰着する。 y[n]= {(1+2√2)(3+2√2)^n-(1-2√2)(3-2√2)^n} / 2√2 で尽くされる。 漸化式はy[k]=6y[k-1]-y[k-2] y[0]=2,y[1]=8,y[-1]=4,y[-3]=128 が既知の解。 y[k]をpで割った余りは周期2^12を持つ y[k]は2^2で割り切れる ⇔ k≡1 (mod 2) y[k]は2^3 で割り切れる ⇔ k≡1 (mod 2^2) ・・・ y[k]が2^12で割り切れる ⇔ k≡957 (mod 2^11) という挙動がある フェルマー素数 p=2^16+1=65537 が証人の役割を果たしてくれる。 k≡957 (mod 2^11) のとき y[k]をpで割った余りは 7697または -7697 となる。 2の冪乗をpで割った余りは65536個のうち32個の剰余類だけを巡回する。 ところが±7697はこの32個の剰余類の巡回に含まれていないから問題が解決する。 ・3^n+22=m^2 x^2-3y^2=-22 で y=±3^n となる解を探すことに帰着。 y[n] = {(5+√3)(2+√3)^n - (5-√3)(2-√3)^n}/2√3 y[2]=27が小さい解。 y[k]は3^3 で割り切れる ⇔ k≡2 (mod 3^3) y[k]は3^4 で割り切れる ⇔ k≡29 (mod 3^4) y[k]は3^5 で割り切れる ⇔ k≡29 (mod 3^5) 少し試行錯誤の痕跡を明かすと、まずy[k]が3^4の周期を持つpを探してp=6317を試した。 (3^3で解が存在するので証人は3^4以上の範囲で探す必要がある) ところが3の冪乗を6317で割った余りは6316個の既約剰余類を全部網羅するので不適 次に3^5の周期を持つpを探すと最初の例と同じ56377に出会った。これが良い証人となった。 52122^7047≡43330≠±1 (mod p) なので問題が解決する。 （[4]の補足のところに書いた判定法を参照。他の例でもこの判定法をつかっている。） ・5^n±19=m^2 x^2-5y^2=±19 の解として考える x+y√5 = ±(1±2√5)*(2+√5)^k の形で全てである。 今回はkの偶奇によって(x^2-5y^2)の符号が切り替わる仕組みになっている。 従って数列 y[k]= {(1+2√5)*(2+√5)^k - (1-2√5)*(2-√5)^k} / 2√5 で考えれば問題の両方の複号をまとめて扱っていることになる。y[1]=5が小さな解。 y[k]≡0 (mod 25) ⇔ k≡21 (mod 25) という挙動がある。 p=3001が良い証人だと判明した。 y[k]をpで割った余りは100を周期に持つ。 なのでy[k]が25で割り切れる時のk、すなわち k≡21,46,72,96 (mod 100) のときのy[k]をpで割った余りを検討することになる。 これは 250, 863, 2751, 2138 の4種類である。 一方で5の冪乗をpで割った余りは250種類を巡回する めでたいことに上記4種類ともこの巡回から外れているので問題が解決する ※ちなみに巡回の周期が偶数のときは、-1が巡回に含まれているので、 Xが巡回から外れていれば-Xも連動的に巡回から外れていることが分かる ・13^n±12=m^2 x^2-13y^2=±12 として考察。 y[k] = [ {(3+√13)/2}^k * (4+√13) - {(3-√13)/2}^k * (4-√13) ] / √13 先と同様にkの偶奇によって問題の符号が切り替わる関係である。 y[-4] = -13, y[-2]=-1, y[-1]=1 が小さいkで見つかる解。 y[k]が169で割り切れる ⇔ k≡22 (mod 169) の挙動がある。 これに対して、p=1803569が良い証人となる。(そこに至る前には677と2029を試して不適だった) y[k]をpで割った余りは169*2を周期に持つ。 y[22]とy[169+22]をpで割った余りは1403063,1319137である。 一方で、13の冪をpで割った余りは1803569個のうち450892個の剰余類を巡回する。 ±1403063,±1319137は巡回から外れている。解決。 これは 5^x+12=13^z の整数解に対する別解となる https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12122462392 （そこにあるようにxが偶数だと判明するので） ・48*10^n-39=m^2 https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14159354364 [これにより各桁が6な三角数は6, 66, 666に限ることを主張することができる] 係数がついているのでnが偶数の場合でも初等的に解決しない。 しかしnの偶奇それぞれについて証人探し法をすることになる。 (a) |x^2-3y^2|=39 (b) |x^2-30y^2|=39 の整数解でyが4*(10の冪)になるものを探すことに帰着。 (a)ではp=89が良い証人となる。 10の冪乗は88の既約剰余類のうち半分の44個を巡回する。 y[k]が25で割り切れるような時y[k]をpで割った余りは6通りあるがすべて巡回から外れている。 (b)ではp=14401が良い証人だった。 10の冪乗は14400の既約剰余類のうち3600個を巡回する。 y[k]が25で割り切れる時、y[k]をpで割った余りは12648で、巡回から外れている。 ・3^n-2=m^2 これはもっと古い時期2014/9/9に私的数学塾に投稿された（HN「空舟」は私です） http://www004.upp.so-net.ne.jp/s_honma/relax/number28.html この数値においては、「証人探し法」と少し違うやり方で証明できた。 そこのa[0]=a[1]=1、 a[k+2]=4*a[k+1]-a[k] が上記のy[k]の役割に相当する。 a[k]が3で割り切れる ⇔ k≡2 (mod 3) a[k]が3^2で割り切れる ⇔ k≡2+3 (mod 3^2) a[k]が3^3で割り切れる ⇔ k≡2+3+3^2 (mod 3^3) a[k]が3^4で割り切れる ⇔ k≡2+3+3^2+3^3 (mod 3^4) ・・・ 右側の条件は、自然に読みとれる規則がずっと続くことが判明するのである。 これによりリンク先の大小の考察で（証人探しを要さずに）問題が解決できる。 ＊どうしてこの数値ではより規則的になるのか 途中で使う方程式 x^2-3y^2=2 の1つの解は x+y√3 = 1-√3 であり これは素イデアル(2)の分解とみなせるのであるが、 (2)はQ(√3)/Qにおいて「分岐」するのである。 つまり (1+√3) と (1-√3) は同一の単項イデアルを与えるのである 実際 (1+√3)/(1-√3) = -(2+√3) は単数である。 a[k] = {(2+√3)^k * (1-√3) - (2-√3)^k * (1+√3)} / 2√3 = [{(2+√3)/(2-√3)}^k - (1+√3)/(1-√3)} * (3と互いに素な部分) / √3 = [{(2+√3)^(2k) - (2+√3) } * (3と互いに素な部分) / √3 形式的に a[k]≡0 ⇔ k≡1/2 であり p進数的に考察すれば分数は「循環展開」されて1/2 = 2+3+3^2+3^3+... である。 あるいは 2+3+3^2+...+3^(k-1) = (3^k+1)/2 ≡1/2 (mod 3^k) と見ても良いかもしれない。 この考察も私のオリジナルのつもりである。 最初に紹介した方法に同様の方法を試みたが数値が違い展開が規則的にならず、 そこで「証人」を探すという方法を思いついた、というのが当時の思考経緯であったように思う。 ・2^n+17=m^2 https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11180552061
[追記 2020/1/26] ツイッターで問題を見かけて、久しぶりにこの方法を適用してみようと思った。 今までの例と比べて、y^2に2という係数がついているが、多少工夫すれば問題がなかった。 今回は2次体の計算や「証人」の探索にはPARI/GPを使った。 ・7^m+1 = 2y^2 の整数解 https://twitter.com/shino_skycrew/status/1220885027489140736 [a] mが偶数の時：x^2+1 = 2y^2 の整数解で、xが7の冪なものを探索する。 [b] mが奇数の時：x^2+7 = 14y^2 の整数解で、xが7の冪なものを探索する。 m=0,1,2が整数解として見つかるが、それ以外にないことの証明である。 ---- [a] まずは2次体の整数論を使って一般解を書く： x^2-2y^2=-1 x+y√2 は単数(1+√2)の奇数冪である。 すなわち A=1+√2, B=1-√2 とおいて x[k]=(A^k+B^k)/2 (kは奇数)が一般解である。 x=1,7のときは、y^2=1,4であり既知の整数解を与える。 x[k]が7で2回以上割り切れるときを考える。 （x[k]を7^2で割ったあまりの周期的な挙動を調べると） x[k]が7^2の倍数の時、k≡21 (mod 42)であることが分かる。 ところが（x[k]を239で割ったあまりの周期的な挙動を調べると） このようなkでは、x[k]は239の倍数にもなることが分かる。 従ってx[k]は7の冪でない。 ---- [b] x^2-14y^2=-7 であるから、 x+y√2は、特殊解(7±2√14)に単数(15+4√14)の冪を掛けたものである。 [(7)を分解した(7+2√14)等がこの2次体で単項素イデアルとかいう仕組みである] すなわち、A=15+4√14, B=15-4√14 とおくと、 x[k]={(7+2√14)*A^k+(7-2√14)*B^k}/2 (kは整数)が一般解である。 k=0の x=7が1つの既知の解である。 x=49のときは、y^2=344となるので整数解を与えない。 xが7^3で割り切れるときについて、 A^49-B^49 の素因数の1つ p=113781078769 が「良い証人」となった。 （x[k]を7^3で割ったあまりの周期的な挙動を調べると） x[k]が7^3で割り切れるとき、k≡24 (mod 49)であることが分かる。 次に、（x[k]をpで割ったあまりの周期的な挙動を調べると） このようなkでは、x[k]をpで割ったあまりは33468890633、80312188136の2種類しかとらないことが分かる。 （例えばk=24のときを試しに確認すると x[k]=1991349783473544754690984427824030087 は 7^3で割り切れて、 これをpで割ったあまりは33468890633である。） ところで（7の冪をpで割ったあまりの周期的な挙動を調べると） q = (p-1)/4 = 28445269692 に対して、7^q≡1 (mod p) となることが分かる。 （従ってx[k]が7の冪だとしたらx^q≡1 (mod p)となるはずである。） ところが、 33468890633^q≡-1 (mod p) 80312188136^q≡-1 (mod p) であるから、上記のkに対するx[k]は7の冪でないことが言えた。 すなわち、x[k]が7^3で割り切れるとき、x[k]は7の冪でない。