自明なもの： X=-Y, Z=-W X=-Z, Y=-W X=-W, Y=-Z 自明でない例： (X,Y,Z,W) = (3,4,5,-6) (X,Y,Z,W) = (1,12,-9,-10) [タクシー数] [1] 既知の点を1つ使って、平面や直線の交点を何回かとることで、パラメータ表示を得た。（詳細は後で） X = (735a4-357a3+203a2-43a+6)b2+(-441a4+350a3-172a2-6a-3)b-196a4+245a3-129a2+15a+9 Y = (441a4+105a3-129a2+35a-4)b2+(-147a4-42a3-172a2+50a-9)b+294a4-301a3+203a2-51a+15 Z = (588a4-399a3+31a2+7a-3)b2+(441a4-350a3+172a2+6a+3)b-245a4+259a3-189a2+57a-18 W = -(882a4-399a3+189a2-37a+5)b2-(-147a4-42a3-172a2+50a-9)b-147a4+49a3+31a2-57a+12 ・検索して見当たるパラメータ表示よりだいぶ煩雑であるが、幾何的解釈が興味深いと思う。 ・検索して見当たるパラメータ表示をこの視点で解釈できるかどうかは分かっていない。 ・逆に、任意の(X,Y,Z,W)を与えられたときに、それを与えるa,bを計算で(2種類)得られることを見る。 （有限個あると思われる特殊な場合の個別検討は省略した・・） ・[Vakil]のThe Rising Seaの11.3.14でP^nの滑らかなn次多様体がuniruledであるという事実を読んだのがきっかけである [2] 追記(5/14)：一旦複素範囲を経由して、もっと良いものを見つけた。構成には[1]と違って自明でない点を使わない。（詳細は後で） X = (u^4+v^4-2*u*v^3+3*u^2*v^2-2*u^3*v+u-2*v) Y = -(u^4+v^4-2*u*v^3+3*u^2*v^2-2*u^3*v+u+v) Z = v^3+u^3+1 W = 2*v^3-3*u*v^2+3*u^2*v-u^3-1 逆にX^3+Y^3+Z^3+W^3=0を満たす比[X:Y:Z:W]は上記の式で u = (X*Z+Y*W-Y*Z) / (Z*Z-Z*W+W*W) v = (X*W-Y*Z) / (Z*Z-Z*W+W*W) とおくことによって得られる。 例えば[X:Y:Z:W]=[3:4:5:6] を得られるのは (u,v)=(-29/91,-38/91)のときで、 実際[X:Y:Z:W]=[342/637:456/637:570/637:-684/637]=[3:4:5:-6] となる。 [3] 追記(8/12) https://twitter.com/potetoichiro/status/1293200580614041600 791^3+812^3=1010^3-1 というのを見かけた。 [2]の式でu=-v とおけばZ=1となり、X^3+Y^3=Z^3±1の自然数解の系列(の1つ)を得る： (9u^4-3u)^3 + (9*u^3-1)^3 = (9u^4)^3 - 1 (9u^4)^3 + (9*u^3+1)^3 = (9u^4+3u)^3 + 1 n=1,2,3,4とおくと： 6^3+8^3=9^3-1, 138^3+71^3=144^3-1, 720^3+242^3=729^3-1, 2292^3+575^3=2304^3-1 9^3+10^3=12^3+1, 144^3+73^3=150^3+1, 729^3+244^3=738^3+1, 2304^3+577^3=2316^3+1 しかし、791^3+812^3=1010^3-1はこの系列では出てこない。 逆算すべてのX,Y,Z,W並べ替えで試したが、u,vが整数になるものはなく、 一番分母が小さくなるのは、X=-1010,Y=791,Z=1,W=812としたときのu=-71/73,v=91/73だった。 整数解を網羅したデータ： https://oeis.org/A050787 https://oeis.org/A050791
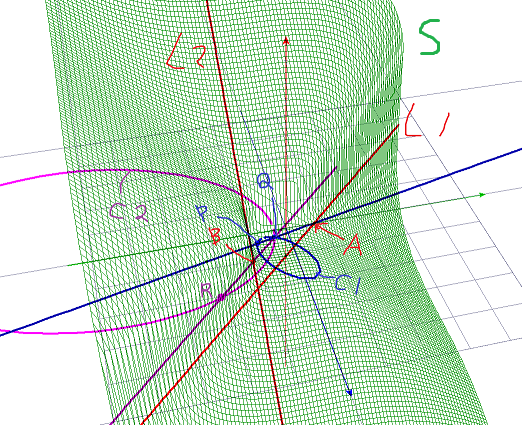
[1]を得た計算 イメージしやすいように、非斉次座標で、3次曲面S: x3+y3+z3+1 = 0 上の点として考える。 この曲面は（実な範囲で）3本の直線を含んでいる。（ちなみにこの3本の直線は同一平面x+y+z+1=0上にある） L1: x=-y, z=-1 L2: x=-z, y=-1 L3: y=-z, x=-1 既知の点を1つ使う。点P:(x,y,z)=(px,py,pz), 例えば(-3/6,-4/6,-5/6)とする。 L1上の点A(a,-a,-1)とPを結ぶ直線は、Sともう1点Qで交わる： 式は平面 (x+y)/(px+py) = (z+1)/(pz+1) 上の直線 (x-a)/(px-a) = (y+a)/(py+a) [L1とPを通る平面と曲面Sの交わりは、直線Sと2次曲線C1をなす。P,Q∈C1⊂S] Qの座標を計算すると以下のようになる： x = -(28a2-11a-3)/(42a2-7a+5) y = -(21a2+11a-4)/(42a2-7a+5) z = -(35a2-7a+6)/(42a2-7a+5) これを、点Q=(qx,qy,qz)とおく。次に、 L2上の点B(b,-b,1)と点Qを結ぶ直線は、Sともう1点Rで交わる： 式は平面 (x+z)/(qx+qz) = (y+1)/(qy+1) 上の直線 (x-b)/(qx-b) = (z+b)/(qz+b) [L2とQを通る平面と曲面Sの交わりは、直線L2と2次曲線C2をなす。Q,R∈C2⊂S] Rの座標を計算すると以下のようになる： x = -((735a4-357a3+203a2-43a+6)b2+(-441a4+350a3-172a2-6a-3)b-196a4+245a3-129a2+15a+9)/((882a4-399a3+189a2-37a+5)b2+(-147a4-42a3-172a2+50a-9)b+147a4-49a3-31a2+57a-12) y = -((441a4+105a3-129a2+35a-4)b2+(-147a4-42a3-172a2+50a-9)b+294a4-301a3+203a2-51a+15)/((882a4-399a3+189a2-37a+5)b2+(-147a4-42a3-172a2+50a-9)b+147a4-49a3-31a2+57a-12) z = -((588a4-399a3+31a2+7a-3)b2+(441a4-350a3+172a2+6a+3)b-245a4+259a3-189a2+57a-18)/((882a4-399a3+189a2-37a+5)b2+(-147a4-42a3-172a2+50a-9)b+147a4-49a3-31a2+57a-12) これが冒頭に紹介したものである。
逆に曲面S上の点 R:(rx,ry,rz) が与えられたとき：
RとL2を通る平面と、PとL1を通る平面の交点を計算する。
平面 (x+z)/(rx+rz) = (y+1)/(ry+1) と
平面 (x+y)/(px+py) = (z+1)/(pz+1) を連立させて、点Q:(qx,qy,qz)を得る。
(3つの候補を得る。そのうち1つはL1とL2の交点(1,-1,-1)であり残り2つが適する)
それから、
QとPを通る直線とL1の交点を求めてaを復元する。
QとRを通る直線とL2の交点を求めてbを復元する。
試しに R=(12,-9,-10)とする。Qを計算すると：
Q: (4/5,3/5,-6/5)
Q: (14/17,7/17,-20/17)
(a-qx)/(px-qx) = (-a-qy)/(py-qy) から a を得て
(b-qx)/(rx-qx) = (-b-qz)/(rz-qz) から b を得る
上記の2つのQからはそれぞれ (a,b)=(1/11,8/3), (1/7,5/2)を得る。
実際上記の長い式にこれらを代入すると目的の点Rを得た。
[メモ] 3D-GRAPES (無料ソフト) に打ち込んだ数式 点P: (-3/6,-4/6,-5/6) 曲面Q: (s,t,Sign(-1-s^3-t^3)(abs(-1-s^3-t^3))^(1/3) ) 直線R: (a,-a,-1) 直線S (s, (s-a)/(Px-a)(Py+a)-a, (s-a)/(Px-a)(Pz+1)-1 ) 曲線T: (-(28a^2-11a-3)/(42a^2-7a+5),-(21a^2+11a-4)/(42a^2-7a+5),-(35a^2-7a+6)/(42a^2-7a+5) ) 直線V:(b,-1,-b) 直線U:(s, (s-b)/(Tx-b)(Ty+1)-1, (s-b)/(Tx-b)(Tz+b)-b ) 曲線A:(-((735a^4-357a^3+203a^2-43a+6)b^2+(-441a^4+350a^3-172a^2-6a-3)b-196a^4+245a^3-129a^2+15a+9)/((882a^4-399a^3+189a^2-37a+5)b^2+(-147a^4-42a^3-172a^2+50a-9)b+147a^4-49a^3-31a^2+57a-12), -((441a^4+105a^3-129a^2+35a-4)b^2+(-147a^4-42a^3-172a^2+50a-9)b+294a^4-301a^3+203a^2-51a+15)/((882a^4-399a^3+189a^2-37a+5)b^2+(-147a^4-42a^3-172a^2+50a-9)b+147a^4-49a^3-31a^2+57a-12), -((588a^4-399a^3+31a^2+7a-3)b^2+(441a^4-350a^3+172a^2+6a+3)b-245a^4+259a^3-189a^2+57a-18)/((882a^4-399a^3+189a^2-37a+5)b^2+(-147a^4-42a^3-172a^2+50a-9)b+147a^4-49a^3-31a^2+57a-12) ) 2020/05/13
[追記]：[2]を得た計算 曲面Sは、複素数範囲では、27本の直線を含む。 そのうちねじれの位置にある2本を利用すると、より簡単な数式で済んだ。 α=(-1+√-3)/2, β=(-1-√-3)/2 とおく。ねじれの位置にある2つの直線上の点： 直線L1 : z=-α, x=-αy 上の点P1 (-uα-vβ,u+vα,-α) 直線L2 : z=-β, x=-βy 上の点P2 (-uβ-uα,u+vβ,-β) をとる。点P1,P2を通る直線と曲面Sとの交点をとれば、3番目の点を得る。 u,vが実数のときP1,P2が複素共役で、3番目の点は実数となる仕組みである。 実際に計算すると：（x^3+y^3+z^3+1=0 と以下を連立させる： L1とP2を通る平面: (z+α)/(-β+α) = (x+αy)/(-β+α)(u+vα), L2とP1を通る平面: (z+β)/(-α+β) = (x+βy)/(-α+β)(u+vβ)） x = (v4-2uv3+3u^2v^2+(-2u3-2)v+u4+u)/(2v3-3uv^2+3u^2v-u3-1) y = -(v4-2uv3+3u^2v^2+(1-2u3)v+u4+u)/(2v3-3uv^2+3u^2v-u3-1) z = (v3+u3+1)/(2v3-3uv^2+3u^2v-u3-1) を得る。 逆にL1上にもL2上にもない点R: (X,Y,Z,1) ∈S は、 RとL1を通る平面と、L2の交点のy座標が u+vβ となるような実数u,vによって復元できる。 計算すると： (z+α)/(Z+α) = (x+αy)/(X+αY), z=-β, x=-βy を連立して u = (Y+XZ-YZ)/(1-Z+Z2) v = (X-YZ)/(1-Z+Z2) を得る。 具体的には例えば(X,Y,Z,1)=(-3/6,-4/6,-5/6,1)とした場合は、u=-29/91,v=-38/91で復元する。 2020/05/14