1.1 x^kの周期と原始根

10^kを7で割ったあまりは周期6で、3,2,6,4,5,1と循環する。
10^kを13で割った余りも周期6で、10,9,12,3,4,1と循環する。
これは10進法において、1/7や1/13の最短循環節が長さ＝6に反映される。
d.1 スクリプトでちょっと遊べると思う。

この節では次の2つのことを主張する。

☆主張１☆
　xのk乗をpで割った余りは、遅くともk=φ(p)の時、1になる。(フェルマーの小定理)
　すなわちφ(p)は(最短周期ではないかもしれないが)必ず周期になる。
　「最短周期はφ(p)の約数でなければならない」と言いかえることもできる。

☆主張２☆
　pが素数のとき、xをうまく選べばk＝φ(p)＝p-1の時初めてx^k≡1(mod p)になる。
　すなわちあるxについて、x^kの値は、p-1が最短周期となる。
＃このようなxをmod pにおける「原始根」とか呼ぶ。
＃そのとき、x^kはp-1個の全部の剰余類を巡回網羅する。

系：pが素数で、kがφ(p)の約数とする。x^k≡1となるxはk個ある。
（∵p=7では、原始根のべき乗列 3,2,6,4,5,1のうち2,4,6番目が3乗して1になる。
　同様にして、一般には原始根のべき乗列のφ(p)/kの倍数番目がk乗して1になる。)

[主張１の説明]
群論のラグランジュの定理の議論による。
・例えば、x^kを7で割ったあまりを考える。xは1,2,3,4,5,6のどれかである。
　xを掛けて言って今まで同じものが現れたら反復するから周期は6以内である。

・これだけでは周期が6の約数とは分からない。仮にxを4回掛けたら元に戻るとする。
　すなわちx≠1,x^2≠1,x^3≠1,x^4≡1 (mod 7)と仮定する。
　x,x^2,x^3,x^4≡1 は異なる4つの数である。よってここに使われない数が2つある。
　それをcとする。cx,cx^2,cx^3,cx^4≡c も同様に4つの異なる数となる。
　これは先の4つの数と全部ばらばらのはずである。しかし8種類もないから矛盾。
（例えばx^2≡cx^3とすると両辺にxを掛けてx^3≡c,これはcの定義に矛盾）

・xをn回掛けたら元に戻るその周期nが6の約数でなければ同様のことが起きる

[主張２の説明]
・a.1 合同式の性質と2.1 円分多項式を使うと分かりやすいと思う。
　p=7を例に見る。フェルマーの小定理より、x^6-1≡0 (mod 7)は解を６個持つ。
　x^6-1＝Φ[1](x)*Φ[2](x)*Φ[3](x)*Φ[6](x)に注意する。
　Φk(x)≡0はφ(k)次式で、高々φ(k)個の解しか持たない。
（∵6＝φ(1)+φ(2)+φ(3)+φ(6)。一般に、Y＝Σφ(y) [yはYの約数] である。）
　ということはフル活用しないといけない。
　つまり6の約数dに対してΦ[d](x)≡0はφ(d)個の解を持つ。
　しかも異なるdでは解は重複しない。
　Φ[6](x)≡0の解はx^6≡1を満たし、Φ1,Φ2,Φ3の時の解ではないからx^2≠1,x^3≠1

p=7とp=13で具体的に様子を見よう。

・p=7の時、x≡3とx≡5が「うまく選べば...」の要件を満たす原始根でる。
　x=3としたときにx^kのとる値を時計回りに並べると次のようになる。

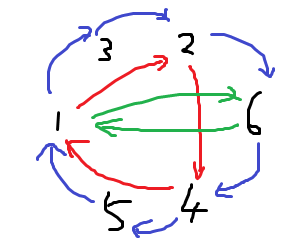
このような図において1を0番目と数えることにすると
k番目の数≡3^kであるから指数法則により以下のようになる。
・k番目の数×j番目の数≡(k+j)番目の数
・k番目の数のj乗≡(k×j)番目の数となる。

ということは、
k番目の数がm乗して初めて1になる ⇔ kをm倍すると初めて6の倍数になる
...と言いかえることができる。いくつかの数字について図と見比べられたい。
＃10^kの様子は、3^kの様子と同じである。確かに6乗で初めて1になる。
(注) (3+7)^k≡3^k (mod 7)が成り立つからである。

また、次も成り立つ。
m乗するとk番目の数になる数がある ⇔ kはmの倍数である
＃m=2の場合は、2≡3^2≡4^2, 4≡2^2≡5^2, 1≡1^2≡6^2 (mod 7)である。
　奇数番目に並んでいる3,6,5については≡( )^2と書けない。

・p=13では2,6,7,11が原始根になる。a=2,a=6の図解を示した。残りは逆回りで得る。

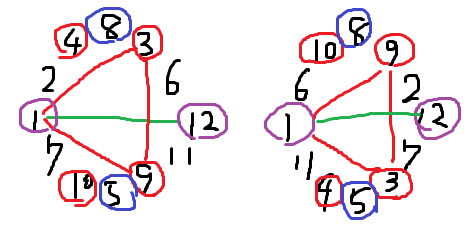
数字の並び順は違うが、dの倍数番目にある数字はどちらの図でもdの倍数番目にある。
＃1,3,9は4N番目にあるから3乗すると1になる。
　また、4乗してこれらの数字になる数字がある。
＃1,8,12,5は3N番目にあるから4乗すると1になる。
　また、3乗してこれらの数字になる数字がある。等...

このように、この図を書けばx^kの様子は分かったと言っていいだろう。

☆7の原始根による列132645...は見覚えがあるかもしれない。
＃6桁の数abcdefが7で割り切れる ⇔ f+3e+2d+6c+4b+5aが7で割り切れる
∵10^kを7で割った余り＝3^kを7で割った余り＝132645...
＃1/7=0.142857... の142857の大小の順番は132645と一致する。
∵なぜなら1桁ずつ繰り上がらせると
　10/7=1.426571...
　100/7=14.265714...
　で小数部分の分子が先と同様に1,3,2,6,4,5の順になるから。