 �u�C�f�[���̌��t�ł̃A���e�B���ʑ��v���L�q���邱�Ƃ��A
�ޑ̘_���̗̂��������Ȃ�[�߂��B
���̃m�[�g�̑O���͂��̂�����̐��������݂�B
������ɐV���������ł����i��������Ȃ��j�̂́A
���̂�������@�Ɏ��ȉ~�Ȑ��ւ́A���r���e�C�g���_�̌��т����ł���B
���������Ӗ��ŁA1�O�̃m�[�g��2�O�̃m�[�g�̓��e�����т���Ƃ����Ӗ����������邩������Ȃ��B
�������S�̓I�ɕ����Ȃ��珑���Ă��邱�Ƃł���̂Ő����͏\���łȂ��B�i�����̂悤�ɁE�E�j
�u�C�f�[���̌��t�ł̃A���e�B���ʑ��v���L�q���邱�Ƃ��A
�ޑ̘_���̗̂��������Ȃ�[�߂��B
���̃m�[�g�̑O���͂��̂�����̐��������݂�B
������ɐV���������ł����i��������Ȃ��j�̂́A
���̂�������@�Ɏ��ȉ~�Ȑ��ւ́A���r���e�C�g���_�̌��т����ł���B
���������Ӗ��ŁA1�O�̃m�[�g��2�O�̃m�[�g�̓��e�����т���Ƃ����Ӗ����������邩������Ȃ��B
�������S�̓I�ɕ����Ȃ��珑���Ă��邱�Ƃł���̂Ő����͏\���łȂ��B�i�����̂悤�ɁE�E�j
���C�f�[���̌��t�ł̃A���e�B���ʑ��� K�̃C�f�[���Q��A_K*�ƕ\�L����B (���)�A���e�B���ʑ��ƂƂ́AA_K*����G^ab�ւ̏����^�ʑ��ŁA �iG^ab�Ƃ�K�̍ő�A�[�x���g��K^ab/K�̃K���A�Q�j �u�Ίp�ʑ�K*��A_K*�̑��̘A�������v���j�Ƃ���悤�Ȃ��̂ł���B �����K=Q�̏ꍇ�ƁAK�����̂̂Ƃ��ɓ��ɋ���������B ker(��)=�u�Ίp�ʑ�K*��A_K*�̑��̘A�������v�� K=Q�̂Ƃ��͗L���f�_�����ׂē����������f�_�����Ȍ�{(a,a,a,...,r)|r>0} K�����̂̂Ƃ��͗L���f�_�����ׂē����������f�_�͔C�� �Ƃ��������Q�ł���B ����ɗL�����A�[�x���g��L/K�ɑ��āA �m�����ʑ��̑��ƁAA_K/ker(��)�`G^ab�̕����Q���Ή�����Ƃ������������邪 �L�q�ɕK�v�Ȓ�`�������̂ŏڂ����q�ׂȂ� ------- �A���e�B���ʑ��Ƃ́A�Ǐ��A���e�B���ʑ��̐ςƂ��ċL�q���邱�Ƃ��ł���B ���ꂼ��̋Ǐ���K_p�̏�@�QK_p*�ɑ��� �Ǐ��A���e�B���ʑ���_p'�FK_p*��G_p^ab �����݂���B �iG_p^ab��K_p�̍ő�A�[�x���g��K_p^ab/K_p�̃K���A�Q�j ������K_p��K�̊g��̂ł��邩��AK^ab_p��K^ab�̊g��ł���A�]���Ďˉe G_p^ab �� G^ab ������B ��_p'�Ƃ��̎ˉe���������邱�ƂŁA��_p�FK_p��G^ab �邱�Ƃ��ł���B A_K*�̌�x�ɑ��āAx��p������x_p�Ƃ����� ���ׂĂ̑f�_p�ɑ����_p(x_p) �̐ςƂ��ă�:A_K*��G^ab ���L�q���邱�Ƃ��ł���B ��̓I�ȋL�q�����������ǂ��B ------- ��K=Q�̏ꍇ�̋�̓I�ȃA���e�B���ʑ��� �f��p�ɑ��ă�_p:K_p��G^ab �͎��̂悤�ɋL�q�����(p�͐��ɑI��) Q�̍ő�A�[�x���g��Q^ab��1�̙p���Ő��������Ƃ�������������A �]����G^ab�̌����L�q����ɂ́A1�̙p���ւ̍�p���L�q����Ηǂ��B �Ep���L���f�_�̂Ƃ��Ax_p=u_p*p^k�ƕ��������(u_p��K_p�̒P���Ap�̔{���łȂ�p�i����) ��_p(x_p)�́F p�Ƒf��n�ɑ���1��n�捪���A����p^k��Ɏʂ��A1��p�p�捪���A����u_p^-1��Ɏʂ��E�E�@ �e�C�g���Q�ƌĂ��T�O���g���Ă���B �Ⴆ�� p=7, u_p=3+7+2*7^2+6*7^3+7^4+.. �Ƃ���7�i���̍�p�� 1��7�捪������5��Ɏʂ� (3^-1��5 (mod 7) �Ȃ̂� u_p^-1��5 (mod 7)) 1��49�捪������5��Ɏʂ��i(3+7)^-1��5 (mod 49)�j 1��343�捪�͂���54��Ɏʂ� ((3+7+2*7^2)^1��5 (mod 343)) �Ƃ�����ɒ�܂�̂ł���B �����͗����I�ł��邱�Ƃ��w�E���Ă����B (w��1��49�捪�Az��1��343�捪�Ƃ���ƁA w�̎ʂ���2�s�ڂ���� w^5 �ł��� ��� w=z^7 ���g����z��z^54�Ɏʂ邱�Ƃ��o�R����� w=z^7�� z^(54*7) �Ɏʂ邱�ƂɂȂ邪 ����͊m����w^5 �Ɠ������ʂɂȂ�A�Ƃ����Ӗ��ŗ����I�ƌĂB) �E(��)�����f�_�ł́A���̑��͍P���ʑ��A���̑��͕��f�����ʑ�(1��n�捪������-1��Ɉڂ�)�E�E�A ����G�c�ȕW��́u�f�������͕s����g��ɍ�p���A�P�������͕���g��ɍ�p����v ����̓��r���e�C�g���_�ɂ���ċ�̓I�ɍ\�����邱�Ƃ��ł��āA����ɂ��Ă͏ڂ����͌�Ő�������B �����ꂪ�A���e�B���ʑ��̐��������Ă��邱�Ƃ��m�F����B �u���ׂĂ̐������ɗL�����{�����Ƃ��ɑ����ς��Ȃ��v�Ƃ�������������B �Ⴆ���ׂĂ̐�����3�{����ƁA ��_3(3)�́A�Ⴆ��1��5�捪��3��Ɏʂ����A��_5(3)���A�����ł������悤�ɍ�p���� �i���������s����u_p��^-1�����Ă���j �i���V�ɂ���Ă͔��̂ق���^-1�����闬�V������炵���j �܂��Ⴆ���ׂĂ̐�����-1�{����ƁA ��_3(-1)�́A1��3�p�捪��-1��Ɏʂ����A�����f�_�̍�p�������ł������B ����U������m�F���Ă��܂�����A���ׂĂ̐������P���ƂȂ��Ă���悤�ȃC�f�[���������l����Ηǂ��B ���Ȃ킿 ��]�Q A_K*/ker(��) �̑�\���Ƃ��āA �i�܂�A���ׂĂ̐����ɓ����L�������|����Ƃ�������ƁA�����������ɐ��̐����|����Ƃ�������ɂ���āj �uA_K*�̌��ł��ׂĂ̐������P���Ŏ������f�_��1�Ȃ��́v���Ƃ邱�Ƃ��ł��邱�Ƃɒ��ڂ���B ���̕����W���i�����Q�ł�����j���i��W���I�ȋL�@�ł��邪�jU_K*�ƕ\�L���Ă݂�B �A���e�B���ʑ��ɂ��AU_K*��G^ab�Ɠ��^�ł���B �Ƃ���U�����ꂽ���^�ʑ� U_K*��G^ab �� ��_U �Ɩ��t���Ă������Ƃɂ���B ------ ���C�f�A���ŋL�q�����ꍇ�Ƃ̔�r�� �����ԑO�ɗޑ̘_�u�`��ǂ�ł������A�C�f�A���ɂ��A���e�B���ʑ��̕����������������Ƃ��������F http://searial.web.fc2.com/aerile_re/artinhasse.txt �ȑO�������������̗�����̃C�f�[���ɂ��A���e�B���ʑ��ʼn��߂��Ă݂�B [��1]��L=Q(i)�ւ̍�p���l�������̂ł���B ���̂悤�ȂƂ��u�L�����g��ɑ���A���e�B���ʑ��v���l���Ă���ƈӎ�����ƍ������ɂ����Ǝv���B �܂� G^ab ���� Gal(L/Q) �ւ̎ˉe������̂� �Ƃ��邢�� ��_U �Ƃ��̎ˉe���������邱�Ƃ� ��[L/K] �FA_K* �� Gal(L/Q) ��_U[L/K] : U_K* �� Gal(L/Q) ���l���邱�Ƃ��ł��Ă����͑S�˂ł���B Gal(L/Q)�͈ʐ�2�̌Q������A��[L/K]���_U[L/K]�̊j�́A�w��2�̕����Q�ł���B Gal(L/Q)�̒P�ʌ��łȂ��ق��Ɏʂ��L�ɔ��ɍ�p�����鐬���́A ��_2(�P��) ��2�ȊO�̑f��p�ɂ�� ��_p(p) �����ł���B i��1��4�捪�ł��邱�ƂƏ�L�̃A���e�B���ʑ��̋L�q���g�����ƂŁA ker(��_U[L/K])�́A�up=2������4N+1�v�Ƃ��������Q�ł��邱�Ƃ�������ł��낤�B(N��Z_2) ���Ȃ݂� ker(��[L/K]) �̋L�q�͏�����₱������ p=2�������A(1+4N)*2^Z���ǂ����E�E�@ p=4N+3������ p�̎w�����������ǂ����E�E�A �������f�_�����́A�����ǂ����E�E�B ���l���āA�@�A�B�̂����������^�ł���悤�ȁAA_K*�̎w��2�̕����Q�ł���B [��2]��1�̌��n13�捪�Ăɂ���=��+��^5+��^8+��^12�ɂ�钆�ԑ�Q(��)���l�������̂ł���B ���l�ɂ��āACl_K�̕����Q�Ɉڂ��čl�����p=13���������ɂȂ�B p=13������(1,5,8,12)�ł���悤�ȕ����Q���A�A���e�B���ʑ���ʂ���Q(��)/Q���Œ肷��G�̕����Q�Ɉڂ�B �C�f�A���I�A���e�B���ʑ��̑�(L/K|p)�́A p����������p�ȃC�f�[���̌��́A�C�f�[���I�A���e�B���ʑ��̑��Ɖ��߂��邱�Ƃ��ł���B �i�����p=13����������1/p�ȃC�f�[���̌��̍s����Ɠ����ł���j �C�f�A���I��I_m/H_m��Gal(L/K)�Ɠ��^�ɂȂ�Ƃ����咣�́A (p=13������(1,5,8,12)�ȕ����Q) �� (L���Œ肷��G�̕����Q) �Ɉڂ邱�Ƃ���U������� �C�f�[���ތQ/(p=13������(1,5,8,12)�ȕ����Q) �� Gal(L/K) = G^ab/(L���Œ肷��G�̕����Q) �̓��^�ɑΉ����� [��4] Q(��-1,��-5)/Q(��-5) �ł͔�P���C�f�A���������B ���̂��ƂɃC�f�[���̂ق��őΉ����錻�ۂ́AQ�̏ꍇ�͉\�ł���������F �u���ׂĂ̐����ɓ����L�����{���邱�Ƃł��ׂĂ̐�����P���ɂ���v �Ƃ������삪�ł��Ȃ��A�Ƃ������ۂ��Ή�����B �Ⴆ��(2,1+��-5)����������2�A�Ƃ����C�f�[���̌��ɑ��āA ���ׂĂ̐������L�����{���Ă��ׂĂ̐�����P���ɂł��Ȃ��B �i�Ⴆ��1/2�{���Ă݂�ƁA���̐����͒P���ɂł��邪�A�����(2,1-��-5)�������P���łȂ��Ȃ�j �u���ׂĂ̐������L�����{���Ă��ׂĂ̐�����P���ɂł��镔���Q�v�́A A_K*�̎w��2�̕����Q���Ȃ��Ă��� ����̃A���e�B���ʑ��̑��ɂ��G^ab�̎w��2�̕����Q�ɑΉ�����g��̂��q���x���g�ޑ� �Ƃ����ł���B ================= ���������̑f�����W���Ƃ̊W�E���ݖ@���� p�p�����_�̒��ԑ�L/K���l����B L/K�̐������̒�`������f(x)���l����B f(x)�̑f�����W���́AL/K�ŕ���f�_��@�Ƃ���@���ŋL�q�����B f(x)=x^2-5 �̏ꍇ�͕���f�_��p=5�݂̂ł���Af(x)�̑f�����W����q�߁}1(mod 5) f(x)=x^2-3 �̏ꍇ�͕���f�_��p=2,3�ł���Af(x)�̑f�����W����q�߁}1(mod 12) f(x)=x^2+x+2 �̏ꍇ�͕���f�_��p=7,���ł���Af(x)�̑f�����W����q��1,2,4 (mod 7)����q��0 ����q��0���K�v�ɂȂ邩�ǂ������A�������f�_�����Ă��邩�ǂ����f���Ă���Ƃ���ł���B�B ���̂悤�ɂ��āA�L�����g��L/K�ɑ����p���l���鎞�ɂ́A ����f�_��@�Ƃ���@���ŁA�f�C�f�A���̕����̗l�q���L�q�����A�Ƃ������ۂ��N����B �i1��p�p�捪�ɂ��g��ł̕���f�_��p�Ɓ��݂̂ł���A ���̒��ԑ̂ɂ��Ă͎��Ȓ��ԑ̂̏ꍇ�͕���f�_��p�̂݁A ���łȂ����ԑ̂̏ꍇ�͕���f�_��p�Ɓ��ł���B�j ����́A�A���e�B���ʑ��̐������g���Ď��̂悤�ɉ��߂ł���B �Ⴆ��p=13���ǂ��������邩�́Ap=13�ɑ���t���x�j�E�X�ʑ���m��Ηǂ��F ���̈ʐ��́A��]�̂̊g�原���ɓ������B����p�����S��������ꍇp�̃t���x�j�E�X�͍P���ʑ��ł���B �����p�����݂̂�p�ő��̐�����1�Ƃ����C�f�[���̌��́A�A���e�B���ʑ��̍s������l���邱�ƂɂȂ�B �A���e�B���ʑ��̐�������Ap�����݂̂�1�ŁA���̐�����1/p�Ƃ����C�f�[���̌��Ɠ����K���A�Q�̌����߂�B ���̐����ł�1/p�͒P��������AL/K�ɑ��Ď����I�ɍ�p����̂́A����f�_�����ł���B ���������킯�ŕ���f�_�ł̗l�q�ł̋L�q�ɋA�����邱�Ƃ��ł���Ƃ����킯�ł���B �ihttp://searial.web.fc2.com/aerile_re/qruitai.html�@�́����ݖ@���Ƃ̊W���̏��ł����������B�j ��������ƁA���ݖ@���Ƃ́A ���Ă���f�_ �� �P������ �ɑ���Ǐ��A���e�B���ʑ�(�����_�̒u���ʑ�)�ƁA ���Ă��Ȃ��f�_ �� ��P������ �ɑ���Ǐ��A���e�B���ʑ�(�t���x�j�E�X�ʑ�)�̊W�ł���B �Ƃ����ӂ��ɗ������邱�Ƃ��ł���B
��������@���g�������̂̋�̓I�ȃA���e�B���ʑ��� K=Q(��-7)�̏ꍇ���ɂ���B ����́A�ȉ~�Ȑ��̐����ł͕W��2,3�͓��ʈ��������̂Ŕ�������������ł���A Q(��-1)��2������̂Ŕ����邵�AQ(��-5)�͐������P���C�f�A������łȂ��̂Ŕ����錋�ʂł���B K�̐�����O��������@�Ɏ��ȉ~�Ȑ���1�FE;y^2+xy=x^3-x^2-2x-1���g���B K^ab��E�̃������_(����O)�Ő��������Ƃ�������������A G^ab�̌����L�q����ɂ́A�����ւ̍�p���L�q����Ηǂ��B K=Q�̂Ƃ��Ɠ��l�ɁAx_p=u_p*��^k�ƕ�������(u_p��K_p�̒P���A�͑f��)�l����̂ł��邪�A �����ŁA�̕����̑I�ѕ��ɑI���̗]�n������A���ꂪ��Ԃ�₱������ǂł������B �}�̂�����-7��@�Ƃ���1,2,4�ɍ����ȕ���{��}�Ƃ��Ē�߂Ă�����y�W���`�z�ƌĂԂ��Ƃɂ���B ���̗R���͌�ōl�@���A��Ɍ��_�ƂȂ�A���e�B���ʑ����L�q���Ă����F�@�A�Ƃ��Ȃ蓯�l�ł���B �Ep=(��)��7�ƌ݂��ɑf�ȂƂ��̕W���`{��}���g���āAx_p=u_p*{��}^k�ƕ������āA p�Ƒf�ȃ��ɑ��郿�����_��{��}^k �{�_�Ɏʂ��Ap�p�����_��u_p^-1�{�_�Ɏʂ��B �Ep=(��-7) �̂Ƃ� x_p=u_7*(��-7)^k�ƕ������āA u_7��1,2,4 (mod ��-7)�Ȃ��=1�A�����łȂ����=-1�Ƃ����B 7�Ƒf�ȃ��ɑ��郿�����_����(��-7)^k�{�_�Ɏʂ��A7�{�_����u_7^-1�{�_�Ɏʂ��B ���A���e�B���ʑ��̐����������Ƃ̊m�F ���ׂĂ̐�����3�{����B3�̕W���`��-3�ł��邱�Ƃɒ��ӂ���B 3�����_�́Ap=(3)������-1�{�_�Ap=(��-7)�����ōĂ�-1�{�_�őł��������B 5�����_�́Ap=(3)������-3�{�_�Ap=(5)������3^-1�{�_�Ap=(��-7)������-1�{�_�őł����������B 7�����_�́Ap=(3)������-3�{�_�Ap=(��-7)������-1*3^-1�{�_�őł����������B �܂��A���ׂĂ̐�����-7�{����ꍇ�B 3�����_�́Ap=(3)������-7^-1�{�_�Ap=(��-7)������-7�{�_�őł����������B ��p�����_�ɂ��g��ŕ���f�_��p,(��-7)�ł���B p�����_��x,y���W�Ő��������g���L�Ap�����_��x���W�����Ő��������g���M�Ƃ����B ����M���A�~���̂̎��̍ő�������̖̂������ʂ����B ���Ȃ킿M/K�ł�(��-7)�͕s����ŁAL/K�ł�(��-7)������Ƃ�������������B [(x,y)��-1�{�_��x���Œ肷�邱�Ƃɒ��ӂ���B �܂�M�́A-1�{�_���Ƃ�ʐ�2�̌���Gal(L/K)�Ő�������镔���Q�ɑΉ����钆�ԑ̂ł���B] ���ǂ�����Ă��̃A���e�B���ʑ���m�邱�Ƃ��ł��邩�B ���ۂɂ́A���̍����͎��ɂ͂܂��ؖ��ł��Ȃ����A �����T�����A�A�[�I�ɋK�������߂čs�����_������������B �������܂łɔF���ł����A�W����T�O�̑S�̑���������x�����B
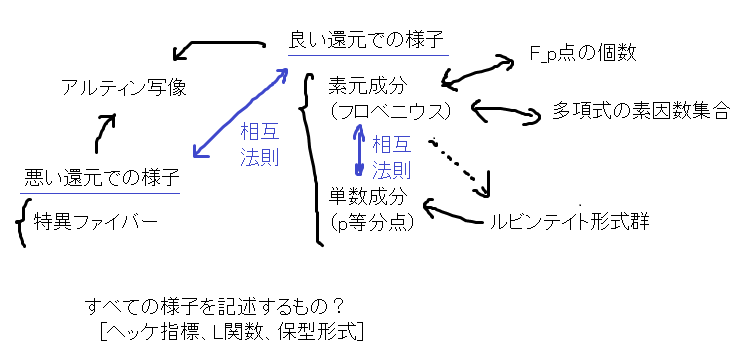
 ���̑S�̑��ɂ���āA�F�������Ȃ萮�����ꂽ�B����ɉ�������Ő����𑱂���B
=================
���t���x�j�E�X�̃g���[�X��
�L�����g�� L/K �ɑ��āA����f�_��p=(��)�A���Ȃ��f�_��q=(��)�Ƃ���
��_p(�P������)�ƁA��_q(�f������)���AL/K�ɑ��Ĕ��ɍ�p���A
�ǂ��炩��������A���e�B���ʑ��̐����ɂ������Е���������̂ł������i���ݖ@���j
p=(��)��(��-7)�ł͂Ȃ��f�_�Ƃ���Bp�Ƒf��n���Ƃ�A(x,y)��n�����_�Ƃ���B
��������ƁAx,y��K���p�ŕs����Ȋg��̂̌��Ƃ����ƂȂ�BP��p�̃m�����Ƃ���B
���̂Ƃ�(x^P,y^P)�́Amod p��(x,y)�́}�Δ{�_�̂ǂ��炩�ɍ����ƂȂ�B�Ƃ�������������B
�i�����ɂȂ�ق�����L�Ły�W���`�z�ƌĂ��ق��ɑΉ����Ă���j
�i�s���� �� �����Ԃ�mod p�ō����łȂ� �� �����������ɂȂ邱�Ƃ͂Ȃ��j
�ǂ���ɍ����ɂȂ邩���L�q����̂��A�u(P���)�t���x�j�E�X�̃g���[�X�v�ł���B
�f�[�^�x�[�X�ł� http://www.lmfdb.org/EllipticCurve/Q/49/a/4
�̃y�[�W�ɂ��� Modular form �� q^p �̌W������������B
(http://www.lmfdb.org/ModularForm/GL2/Q/holomorphic/49/2/a/a/)
�Ⴆ��q^23�̌W����8�ŁAq^37�̌W����-6�ł��邱�Ƃ́A
-4�}��-7��3�}2��-7�͕W���`�ł͂Ȃ��A4�}��-7��-3�}2��-7���W���`�ł��邱�ƂɑΉ�����B
��Љ���悤�Ɂ}�̂����Amod ��-7��@�Ƃ��ĕ�����]�ɂȂ�ق����I���̂ł������E�E��
�ǂ����Ă����Ȃ�̂��ɂ��Ă悭�[���̂��������͂܂��������Ă��Ȃ����A
�t���x�j�E�X�̃g���[�X�ƌ��т��T���I�Ȏ��_�����܂ł�3�F�������B
[1] F_p�_�̌�
[2] �������̑f�����W��
[3] ���r���e�C�g�`���Q
�����͒T���I�Ȃ��̂ŁA�t���x�j�E�X�̃g���[�X��m����@�Ƃ��Ẳ�㈐��͎����Ă��Ȃ��Ǝv���B
���ɉ�㈓I�ɂȂ蓾�邩������Ȃ����_�̌��͂��������邪�A�܂�����������Ă��Ȃ��B
[4] ���كt�@�C�o�[
[5] �w�b�P�w�W�AL���A��1(N)��new cusp form
===========
[1] �̓��t�V�F�b�c�̐Ռ����ɂ����̂ł���B
(E��F_p^k��̓_�̌�) = 1-tr(A^k)+p^k �����藧�̂ł������B
�Ȃ̂ŗL���̏�̓_�̌��𐔂��邱�ƂŁA�ʂɃg���[�X�邱�Ƃ��ł���B
===========
[2] �������̑f�����W�����g�������_
����͑O��̃m�[�g�ōl�@�������̂ł���B
3�����_��y���W�̒�`��������F(y)�Ƃ���B
F(y)=27*y^8+27*y^7-378*y^6+441*y^5-126*y^4+441*y^3-378*y^2+174*y-463
F(y)��3�ȊO�̑f����(Q(��-7)�̐����ŕ�������)�ׂ�ƁA
���̑f�����́A�W���`{��}��3A+1�^�ɂȂ���̂Ɍ�����B
�����Ȃ邱�Ƃ͗ޑ̘_�ɂ���Ċ��҂ł�����̂��Ǝv���Ă���B
���ۂɑf�������������ׂ�A�W���`���ǂ���߂���̋L�q�����藧���𐄑��ł���B
�Ⴆ��F(y)�̑f�����ɂ� 4+3��-7 �� 5-6��-3 �������B
������ 3A+1 �^ �Ƃ݂Ȃ����߂ɂ́A�����́y�W���`�z��
�O�҂�4+3��-7�A��҂� -5+6��-3 �̂ق��łȂ��Ă͂Ȃ�Ȃ��B
�������������̑f�����Œ��ׂ邱�ƂŁA�K���𐄑����Ă������Ƃ��ł���B
���̌��ʂ́A(mod ��-7)�ŕ�����]�ɂȂ�ق�(1,2,4�ɍ���)���W���`�Ƃ������ʂł������B
����́A�ȉ~�Ȑ��i�̓��^�ށj�Ɉˑ�����B
����������@�����ȉ~�Ȑ��ł��A���^�łȂ�����(twist�ƌĂ��)���Ƃ�ƁA
������L�q���鎞�̕W���`�̒�ߕ����ς��B
����́A3�����̐�������g��̂��������Ȃ�����ł���B
========
��isogeny�ɂ��Ⴂ�̗l�q�̗�i�Čf�j��
���̘b����l�@���Ĉ�ԍŏ��Ɏ�������̗�́AZ[��-2]��������@�Ɏ��ȉ~�Ȑ�y^2=x^3-30*x-56���g�����B
���̑ȉ~�Ȑ��ɑΉ�����y�W���`�z�͕��G������(w=��-2�Ƃ����Ă���)�F
q�߁}1 (mod 3) �Ȃ�� {q}��1,3, -1�}w,-3+2w (mod 4w)
q�߁}w (mod 3) �Ȃ�� {q}��-1,-3, 1�}w,3+2w (mod 4w)
�����ŕW���`���߂�̂�w�̙p�Ŋ������]����g�����Ƃ͗\�z����邪3�Ŋ������]����g���̂��ӊO�������B
�O��̃m�[�g�ł�isogeny�ɂ��Ⴂ�Ƃ��Đ����������e��������x�������Ă����B
database�ɂ��Ƃ��̑ȉ~�Ȑ�E:y^2=x^3-30*x-56�̓����2304=2^8*3^2�ł���A
����������@�����ʂ̑ȉ~�Ȑ�E':y^2 = x^3+x^2-3x+1�̓����256=2^8�ł���B
E'�ɕt������W���`��mod 4w�������g���ċL�q�����B
�ihttp://searial.web.fc2.com/aerile_re/qheihou.html ��isogeny a�Ə��������́j
E��E'�́AK(��-3)�㓯�^�ł���B
��̓I�ɂ�E��E'��y��(y*��-3)�ɕς��������� -3*y^2=x^3+x^2-3x+1 �Œ�܂�ȉ~�Ȑ��Ɠ��^�ł���B
�i���ۂ��̎��� x=(X+1)/3,y=Y/9�Ƃ�����E�̎���j
-3��mod (��)�ŕ�����]�̂Ƃ� E,E'�̕W���`�Ɠ�����
-3��mod (��)�ŕ������]�̂Ƃ� E,E'�̕W���`�͕������t
�Ƃ����W�ƂȂ�
================
[3] �`���Q�i���r���e�C�g���_�j
�i���̉��߂������Ă��āA��������������e�����m�łȂ���������Ȃ��j
���Ǐ��A���e�B���ʑ��̕W����Čf����
�u�f�������͕s����g��ɍ�p���A�P�������͕���g��ɍ�p����v
��^k�͕s����g��ɑ��ăt���x�j�E�X�ʑ��Ƃ��ċL�q�ł����̂ł������B
���r���e�C�g���_�́u�P�������͕���g��ɍ�p����v�̕������L�q������̂ł���B
�p����F(X,Y)���`���Q�ł�������͎��̂悤�Ȃ��̂ŁF
�EF(X,Y) = X+Y+(2���ȏ�̍�)
�EF(X,F(Y,Z)) = F(F(X,Y),Z)
�EF(X,i(X)) = 0 �ƂȂ� i(X)�����݂���
�EF(X,Y)=F(Y,X)
�`���Q (�Ⴆ�� F(X,Y)=X+Y+XY ) �ɑ��āua�{�������vf_a���`���邱�Ƃ��ł���F
����� f_a(X) = aX+(X��2���ȏ�̍�) �ƂȂ�悤��f_a�ŁA
F(f_a(X),f_a(Y)) = f_a(F(X,Y)) �����悤�Ȃ��̂Ƃ��ėB�ꌈ�܂�B
��L�̗�ł� f_a(X) = (1+X)^a-1 �ł���B
�����Ńm����p�����f�C�f�A��(��)�ɑ���
f_��(X) �� X^p (mod ��) �������ɁA���̌`���Q��(�ɂ��)���r���e�C�g�`���Q�ł���Ƃ����B
�i���ׂĂ̌`���Q�����r���e�C�g�`���Q�ɂȂ蓾��킯�ł͂Ȃ��Ɨ������Ă���B
�Ⴆ��F(X,Y)�Ƃ��Ēʏ�̉��@ X+Y ���Ƃ����ꍇ�̓��r���e�C�g�`���Q�ɂȂ�Ȃ��Ǝv���B�j
F(X,Y)��(�ɂ��)���r���e�C�g�`���Q�ł������Ƃ���ƁA
����ɂ���ċǏ��A���e�B���ʑ��̒P���������L�q���邱�Ƃ��ł���Ƃ����̂����r���e�C�g���_�ł���F
f_��(X)�̍����A�u�i���r���e�C�g�I�jp�����_�v�ƌĂԂ��Ƃɂ���B
f_��^2(X)���̍��ɂ���āu�i���r���e�C�g�I�jp�p�����_�v���l���邱�Ƃ��ł���B
�i����炪����g��ł���B�j
���w�肳��Ă���̂ŁAx_p��K_p*�� u_p*��^k�ɕ�������܂��āA
�Ǐ��A���e�B���ʑ��̒P��������_p(u_p)��
�i���r���e�C�g�I�jp�p�����_�ɑ��āA�uu_p^-1�{�������v�Ƃ��č�p����
�ƋL�q���邱�Ƃ��ł���B
===========
����̓I�Ȍ`���Q��
Q_p�̗ޑ̘_�́A�`���Q F(X,Y)=X+Y+XY ���g���ċL�q���邱�Ƃ��ł���B
���r���e�C�g�Ip�p�����_�F(1+X)^(p^k)-1 �̍��́A�ʏ��1��p�p�捪�ɑΉ����A
�ua�{�������v (1+X)^a-1 �́Aa��ʑ��ɑΉ����邱�Ƃ���A
�ʏ��Q��̗ޑ̘_�̋L�q���Č������B
���̗̂ޑ̘_�́A�ȉ~�Ȑ��ɕt������`���Q�ŋL�q���邱�Ƃ��ł���B
���C�G���V���g���X�̕W���`����t=-x/y, s=-1/y �ƕϐ��ϊ������
�ʏ�̖������_���A���_s=t=0�Ɉڂ�As=t^3(1+at+bt^2+...) �ƙp�����W�J�����B
(t1,s1)��(t2,s2)�̑ȉ~�Ȑ��I�Șa��(t3,s3)�Ƃ�����
t3 = t1+t2+(t1,t2��2���ȏ�)�ƓW�J���邱�Ƃ��ł��Ă��ꂪ�`���Q�ƂȂ�B
http://homepages.warwick.ac.uk/~masiao/maths/lecturenotes/ellipticnotes.pdf
��Lecture 11 �Ȃǂɂ��������ڂ�������������B(�V���o�[�}���ł��ǂ����ǁE�E)
���̓W�J����̓I�Ɍv�Z����A
�Ⴆ��=2+��-7�ɑ���u2+��-7�{�������vf_��(X)�́A
f_��(X) = (2+��-7)X + (X��2���ȏ�̍�) ��
f_��(X) �� X^11 (mod (��)) �����������Ƃ��ē�����Ǝv���B
�������A���̓W�J�����ۂɓ��悤�Ƃ��鎎�݂́A�v�Z�@�̌��E�ɂ���ĒB���ł��Ȃ������B
�Ȃ̂ł���͂ނ��둼�̏���z������錋�ʂł���B
�����ł���A��L��Q�̏ꍇ�Ɠ����悤�ɂ��āA���̏�̗ޑ̘_���Č������Ǝv���B
���ۂɌv�Z�ł��Ă��Ȃ��Ƃ����S�c��͂��邯��ǁA
���̎��_�ɂ����
�u�Ǐ��A���e�B���ʑ����t���x�j�E�X�̃g���[�X�ɋA�������v
�Ƃ��������ɂ��āA�m���ȗ��_�I�ȍ���������ł���B
�i���������ꂪ7��@�Ƃ���K���ŋL�q�����Ƃ��������̊m���ȍ����͂܂������Ă��Ȃ��j
===============
[4] ���كt�@�C�o�[
�����Ɏg�����ȉ~�Ȑ��ł́A�K����7��@�Ƃ�����̂ł������B
�uisogeny�ɂ��Ⴂ�̗l�q�̗�v�Ō���悤�ɁA����͂��낢��ȃp�^�[�������蓾��B
�ǂ���瓱��Ƃ������̂��W���Ă���炵�����Ƃ�������B
����́A�����Ҍ��ubad reduction�v�ł���B
�Ⴆ��y^2=x^3-30*x-56 �� mod 3 �Ҍ������ y^2��x^3+1��(x+1)^3 �ł���A
����͊m����cusp�^�̓��ًȐ��ŁA�܂� p=3 �ň����Ҍ��������Ă���B
mod 2�Ҍ��ł́Ay^2=x^3 �Ȃ̂ŁA����������Ҍ��ł���B
���̑ȉ~�Ȑ��ł́A�����Ҍ������f�_�͂���2�����ł���B
�ʂ̗�Ay^2+xy=x^3-x^2-2x-1 �ł� p=7 �ł݈̂����Ҍ������B(�v�Z�͏ȗ�)
�f�[�^�x�[�X�T�C�g������ƁA�����Ҍ��ł̃t�@�C�o�[�̎�ނ������Ă���B
http://www.lmfdb.org/EllipticCurve/Q/2304/h/2
prime 2 �ł� Kodaira symbol �� III �Ə����Ă�����
prime 3 �ł� Kodaira symbol �� I_0* �Ə����Ă���B
�����Ҍ��ł̗l�q��������A�ǂ��Ҍ��ł̗l�q��������i���ݖ@���j
�ނ���A�����Ҍ��ł̗l�q���A�ǂ��Ҍ��ł̗l�q���x�z���Ă���Ƃ������_������B
���������̓��كt�@�C�o�[�Ƃ����T�O���Ȃ��Ȃ��悭�����炸�ɂ���B
��������ƗႦ�� https://arxiv.org/abs/0907.0298
�Ƃ������������肢�낢�돑���Ă��邯�ǂ܂��ǂ�������Ȃ��B
=========
[5] �w�b�P�w�W�AL���A�ی^�`��
�E�w�b�P�w�W�̂悤�ȃL�[���[�h�Œ��ׂ�ƁA�����L�q�����悤�ȋK�������y����Ă���Q&A�ɏo�����
https://math.stackexchange.com/questions/2532404/what-is-the-grossencharacter-of-this-cm-curve
�E�w�W������AL����ی^�`�������т��炵��
�E����(conductor)N�͓��كt�@�C�o�[�̗l�q�ƊW���鐔�ł���B
�@�Ή�����ی^�`���́A����N�ɑΉ����郡1(N)��new cusp form�ɂȂ�炵���B
�Ƃ����悤�Ȏ��������Ȃ�ƂȂ������������ǁA�����ǂ����т��Ă���̂��͂܂��ǂ�������Ȃ��B
========= 2019/4/5
���̑S�̑��ɂ���āA�F�������Ȃ萮�����ꂽ�B����ɉ�������Ő����𑱂���B
=================
���t���x�j�E�X�̃g���[�X��
�L�����g�� L/K �ɑ��āA����f�_��p=(��)�A���Ȃ��f�_��q=(��)�Ƃ���
��_p(�P������)�ƁA��_q(�f������)���AL/K�ɑ��Ĕ��ɍ�p���A
�ǂ��炩��������A���e�B���ʑ��̐����ɂ������Е���������̂ł������i���ݖ@���j
p=(��)��(��-7)�ł͂Ȃ��f�_�Ƃ���Bp�Ƒf��n���Ƃ�A(x,y)��n�����_�Ƃ���B
��������ƁAx,y��K���p�ŕs����Ȋg��̂̌��Ƃ����ƂȂ�BP��p�̃m�����Ƃ���B
���̂Ƃ�(x^P,y^P)�́Amod p��(x,y)�́}�Δ{�_�̂ǂ��炩�ɍ����ƂȂ�B�Ƃ�������������B
�i�����ɂȂ�ق�����L�Ły�W���`�z�ƌĂ��ق��ɑΉ����Ă���j
�i�s���� �� �����Ԃ�mod p�ō����łȂ� �� �����������ɂȂ邱�Ƃ͂Ȃ��j
�ǂ���ɍ����ɂȂ邩���L�q����̂��A�u(P���)�t���x�j�E�X�̃g���[�X�v�ł���B
�f�[�^�x�[�X�ł� http://www.lmfdb.org/EllipticCurve/Q/49/a/4
�̃y�[�W�ɂ��� Modular form �� q^p �̌W������������B
(http://www.lmfdb.org/ModularForm/GL2/Q/holomorphic/49/2/a/a/)
�Ⴆ��q^23�̌W����8�ŁAq^37�̌W����-6�ł��邱�Ƃ́A
-4�}��-7��3�}2��-7�͕W���`�ł͂Ȃ��A4�}��-7��-3�}2��-7���W���`�ł��邱�ƂɑΉ�����B
��Љ���悤�Ɂ}�̂����Amod ��-7��@�Ƃ��ĕ�����]�ɂȂ�ق����I���̂ł������E�E��
�ǂ����Ă����Ȃ�̂��ɂ��Ă悭�[���̂��������͂܂��������Ă��Ȃ����A
�t���x�j�E�X�̃g���[�X�ƌ��т��T���I�Ȏ��_�����܂ł�3�F�������B
[1] F_p�_�̌�
[2] �������̑f�����W��
[3] ���r���e�C�g�`���Q
�����͒T���I�Ȃ��̂ŁA�t���x�j�E�X�̃g���[�X��m����@�Ƃ��Ẳ�㈐��͎����Ă��Ȃ��Ǝv���B
���ɉ�㈓I�ɂȂ蓾�邩������Ȃ����_�̌��͂��������邪�A�܂�����������Ă��Ȃ��B
[4] ���كt�@�C�o�[
[5] �w�b�P�w�W�AL���A��1(N)��new cusp form
===========
[1] �̓��t�V�F�b�c�̐Ռ����ɂ����̂ł���B
(E��F_p^k��̓_�̌�) = 1-tr(A^k)+p^k �����藧�̂ł������B
�Ȃ̂ŗL���̏�̓_�̌��𐔂��邱�ƂŁA�ʂɃg���[�X�邱�Ƃ��ł���B
===========
[2] �������̑f�����W�����g�������_
����͑O��̃m�[�g�ōl�@�������̂ł���B
3�����_��y���W�̒�`��������F(y)�Ƃ���B
F(y)=27*y^8+27*y^7-378*y^6+441*y^5-126*y^4+441*y^3-378*y^2+174*y-463
F(y)��3�ȊO�̑f����(Q(��-7)�̐����ŕ�������)�ׂ�ƁA
���̑f�����́A�W���`{��}��3A+1�^�ɂȂ���̂Ɍ�����B
�����Ȃ邱�Ƃ͗ޑ̘_�ɂ���Ċ��҂ł�����̂��Ǝv���Ă���B
���ۂɑf�������������ׂ�A�W���`���ǂ���߂���̋L�q�����藧���𐄑��ł���B
�Ⴆ��F(y)�̑f�����ɂ� 4+3��-7 �� 5-6��-3 �������B
������ 3A+1 �^ �Ƃ݂Ȃ����߂ɂ́A�����́y�W���`�z��
�O�҂�4+3��-7�A��҂� -5+6��-3 �̂ق��łȂ��Ă͂Ȃ�Ȃ��B
�������������̑f�����Œ��ׂ邱�ƂŁA�K���𐄑����Ă������Ƃ��ł���B
���̌��ʂ́A(mod ��-7)�ŕ�����]�ɂȂ�ق�(1,2,4�ɍ���)���W���`�Ƃ������ʂł������B
����́A�ȉ~�Ȑ��i�̓��^�ށj�Ɉˑ�����B
����������@�����ȉ~�Ȑ��ł��A���^�łȂ�����(twist�ƌĂ��)���Ƃ�ƁA
������L�q���鎞�̕W���`�̒�ߕ����ς��B
����́A3�����̐�������g��̂��������Ȃ�����ł���B
========
��isogeny�ɂ��Ⴂ�̗l�q�̗�i�Čf�j��
���̘b����l�@���Ĉ�ԍŏ��Ɏ�������̗�́AZ[��-2]��������@�Ɏ��ȉ~�Ȑ�y^2=x^3-30*x-56���g�����B
���̑ȉ~�Ȑ��ɑΉ�����y�W���`�z�͕��G������(w=��-2�Ƃ����Ă���)�F
q�߁}1 (mod 3) �Ȃ�� {q}��1,3, -1�}w,-3+2w (mod 4w)
q�߁}w (mod 3) �Ȃ�� {q}��-1,-3, 1�}w,3+2w (mod 4w)
�����ŕW���`���߂�̂�w�̙p�Ŋ������]����g�����Ƃ͗\�z����邪3�Ŋ������]����g���̂��ӊO�������B
�O��̃m�[�g�ł�isogeny�ɂ��Ⴂ�Ƃ��Đ����������e��������x�������Ă����B
database�ɂ��Ƃ��̑ȉ~�Ȑ�E:y^2=x^3-30*x-56�̓����2304=2^8*3^2�ł���A
����������@�����ʂ̑ȉ~�Ȑ�E':y^2 = x^3+x^2-3x+1�̓����256=2^8�ł���B
E'�ɕt������W���`��mod 4w�������g���ċL�q�����B
�ihttp://searial.web.fc2.com/aerile_re/qheihou.html ��isogeny a�Ə��������́j
E��E'�́AK(��-3)�㓯�^�ł���B
��̓I�ɂ�E��E'��y��(y*��-3)�ɕς��������� -3*y^2=x^3+x^2-3x+1 �Œ�܂�ȉ~�Ȑ��Ɠ��^�ł���B
�i���ۂ��̎��� x=(X+1)/3,y=Y/9�Ƃ�����E�̎���j
-3��mod (��)�ŕ�����]�̂Ƃ� E,E'�̕W���`�Ɠ�����
-3��mod (��)�ŕ������]�̂Ƃ� E,E'�̕W���`�͕������t
�Ƃ����W�ƂȂ�
================
[3] �`���Q�i���r���e�C�g���_�j
�i���̉��߂������Ă��āA��������������e�����m�łȂ���������Ȃ��j
���Ǐ��A���e�B���ʑ��̕W����Čf����
�u�f�������͕s����g��ɍ�p���A�P�������͕���g��ɍ�p����v
��^k�͕s����g��ɑ��ăt���x�j�E�X�ʑ��Ƃ��ċL�q�ł����̂ł������B
���r���e�C�g���_�́u�P�������͕���g��ɍ�p����v�̕������L�q������̂ł���B
�p����F(X,Y)���`���Q�ł�������͎��̂悤�Ȃ��̂ŁF
�EF(X,Y) = X+Y+(2���ȏ�̍�)
�EF(X,F(Y,Z)) = F(F(X,Y),Z)
�EF(X,i(X)) = 0 �ƂȂ� i(X)�����݂���
�EF(X,Y)=F(Y,X)
�`���Q (�Ⴆ�� F(X,Y)=X+Y+XY ) �ɑ��āua�{�������vf_a���`���邱�Ƃ��ł���F
����� f_a(X) = aX+(X��2���ȏ�̍�) �ƂȂ�悤��f_a�ŁA
F(f_a(X),f_a(Y)) = f_a(F(X,Y)) �����悤�Ȃ��̂Ƃ��ėB�ꌈ�܂�B
��L�̗�ł� f_a(X) = (1+X)^a-1 �ł���B
�����Ńm����p�����f�C�f�A��(��)�ɑ���
f_��(X) �� X^p (mod ��) �������ɁA���̌`���Q��(�ɂ��)���r���e�C�g�`���Q�ł���Ƃ����B
�i���ׂĂ̌`���Q�����r���e�C�g�`���Q�ɂȂ蓾��킯�ł͂Ȃ��Ɨ������Ă���B
�Ⴆ��F(X,Y)�Ƃ��Ēʏ�̉��@ X+Y ���Ƃ����ꍇ�̓��r���e�C�g�`���Q�ɂȂ�Ȃ��Ǝv���B�j
F(X,Y)��(�ɂ��)���r���e�C�g�`���Q�ł������Ƃ���ƁA
����ɂ���ċǏ��A���e�B���ʑ��̒P���������L�q���邱�Ƃ��ł���Ƃ����̂����r���e�C�g���_�ł���F
f_��(X)�̍����A�u�i���r���e�C�g�I�jp�����_�v�ƌĂԂ��Ƃɂ���B
f_��^2(X)���̍��ɂ���āu�i���r���e�C�g�I�jp�p�����_�v���l���邱�Ƃ��ł���B
�i����炪����g��ł���B�j
���w�肳��Ă���̂ŁAx_p��K_p*�� u_p*��^k�ɕ�������܂��āA
�Ǐ��A���e�B���ʑ��̒P��������_p(u_p)��
�i���r���e�C�g�I�jp�p�����_�ɑ��āA�uu_p^-1�{�������v�Ƃ��č�p����
�ƋL�q���邱�Ƃ��ł���B
===========
����̓I�Ȍ`���Q��
Q_p�̗ޑ̘_�́A�`���Q F(X,Y)=X+Y+XY ���g���ċL�q���邱�Ƃ��ł���B
���r���e�C�g�Ip�p�����_�F(1+X)^(p^k)-1 �̍��́A�ʏ��1��p�p�捪�ɑΉ����A
�ua�{�������v (1+X)^a-1 �́Aa��ʑ��ɑΉ����邱�Ƃ���A
�ʏ��Q��̗ޑ̘_�̋L�q���Č������B
���̗̂ޑ̘_�́A�ȉ~�Ȑ��ɕt������`���Q�ŋL�q���邱�Ƃ��ł���B
���C�G���V���g���X�̕W���`����t=-x/y, s=-1/y �ƕϐ��ϊ������
�ʏ�̖������_���A���_s=t=0�Ɉڂ�As=t^3(1+at+bt^2+...) �ƙp�����W�J�����B
(t1,s1)��(t2,s2)�̑ȉ~�Ȑ��I�Șa��(t3,s3)�Ƃ�����
t3 = t1+t2+(t1,t2��2���ȏ�)�ƓW�J���邱�Ƃ��ł��Ă��ꂪ�`���Q�ƂȂ�B
http://homepages.warwick.ac.uk/~masiao/maths/lecturenotes/ellipticnotes.pdf
��Lecture 11 �Ȃǂɂ��������ڂ�������������B(�V���o�[�}���ł��ǂ����ǁE�E)
���̓W�J����̓I�Ɍv�Z����A
�Ⴆ��=2+��-7�ɑ���u2+��-7�{�������vf_��(X)�́A
f_��(X) = (2+��-7)X + (X��2���ȏ�̍�) ��
f_��(X) �� X^11 (mod (��)) �����������Ƃ��ē�����Ǝv���B
�������A���̓W�J�����ۂɓ��悤�Ƃ��鎎�݂́A�v�Z�@�̌��E�ɂ���ĒB���ł��Ȃ������B
�Ȃ̂ł���͂ނ��둼�̏���z������錋�ʂł���B
�����ł���A��L��Q�̏ꍇ�Ɠ����悤�ɂ��āA���̏�̗ޑ̘_���Č������Ǝv���B
���ۂɌv�Z�ł��Ă��Ȃ��Ƃ����S�c��͂��邯��ǁA
���̎��_�ɂ����
�u�Ǐ��A���e�B���ʑ����t���x�j�E�X�̃g���[�X�ɋA�������v
�Ƃ��������ɂ��āA�m���ȗ��_�I�ȍ���������ł���B
�i���������ꂪ7��@�Ƃ���K���ŋL�q�����Ƃ��������̊m���ȍ����͂܂������Ă��Ȃ��j
===============
[4] ���كt�@�C�o�[
�����Ɏg�����ȉ~�Ȑ��ł́A�K����7��@�Ƃ�����̂ł������B
�uisogeny�ɂ��Ⴂ�̗l�q�̗�v�Ō���悤�ɁA����͂��낢��ȃp�^�[�������蓾��B
�ǂ���瓱��Ƃ������̂��W���Ă���炵�����Ƃ�������B
����́A�����Ҍ��ubad reduction�v�ł���B
�Ⴆ��y^2=x^3-30*x-56 �� mod 3 �Ҍ������ y^2��x^3+1��(x+1)^3 �ł���A
����͊m����cusp�^�̓��ًȐ��ŁA�܂� p=3 �ň����Ҍ��������Ă���B
mod 2�Ҍ��ł́Ay^2=x^3 �Ȃ̂ŁA����������Ҍ��ł���B
���̑ȉ~�Ȑ��ł́A�����Ҍ������f�_�͂���2�����ł���B
�ʂ̗�Ay^2+xy=x^3-x^2-2x-1 �ł� p=7 �ł݈̂����Ҍ������B(�v�Z�͏ȗ�)
�f�[�^�x�[�X�T�C�g������ƁA�����Ҍ��ł̃t�@�C�o�[�̎�ނ������Ă���B
http://www.lmfdb.org/EllipticCurve/Q/2304/h/2
prime 2 �ł� Kodaira symbol �� III �Ə����Ă�����
prime 3 �ł� Kodaira symbol �� I_0* �Ə����Ă���B
�����Ҍ��ł̗l�q��������A�ǂ��Ҍ��ł̗l�q��������i���ݖ@���j
�ނ���A�����Ҍ��ł̗l�q���A�ǂ��Ҍ��ł̗l�q���x�z���Ă���Ƃ������_������B
���������̓��كt�@�C�o�[�Ƃ����T�O���Ȃ��Ȃ��悭�����炸�ɂ���B
��������ƗႦ�� https://arxiv.org/abs/0907.0298
�Ƃ������������肢�낢�돑���Ă��邯�ǂ܂��ǂ�������Ȃ��B
=========
[5] �w�b�P�w�W�AL���A�ی^�`��
�E�w�b�P�w�W�̂悤�ȃL�[���[�h�Œ��ׂ�ƁA�����L�q�����悤�ȋK�������y����Ă���Q&A�ɏo�����
https://math.stackexchange.com/questions/2532404/what-is-the-grossencharacter-of-this-cm-curve
�E�w�W������AL����ی^�`�������т��炵��
�E����(conductor)N�͓��كt�@�C�o�[�̗l�q�ƊW���鐔�ł���B
�@�Ή�����ی^�`���́A����N�ɑΉ����郡1(N)��new cusp form�ɂȂ�炵���B
�Ƃ����悤�Ȏ��������Ȃ�ƂȂ������������ǁA�����ǂ����т��Ă���̂��͂܂��ǂ�������Ȃ��B
========= 2019/4/5